A Statistical View of Deep Learning (I): Recursive GLMs

Deep learningand the use of deep neural networks [1] are now established as a key tool for practical machine learning. Neural networks have an equivalence with many existing statistical and machine learning approaches and I would like to explore one of these views in this post. In particular, I'll look at the view of deep neural networks as recursive generalised linear models (RGLMs). Generalised linear models form one of the cornerstones of probabilistic modelling and are used in almost every field of experimental science, so this connection is an extremely useful one to have in mind. I'll focus here on what are called feedforward neural networks and leave a discussion of the statistical connections to recurrent networks to another post.

Generalised Linear Models

The basic linear regressionmodel is a linear mapping from P-dimensional input features (or covariates) x, to a set of targets (or responses) y, using a set of weights (or regression coefficients) β and a bias (offset) β0 . The outputs can also by multivariate, but I'll assume they are scalar here. The full probabilistic model assumes that the outputs are corrupted by Gaussian noise of unknown variance σ².

η=β⊤x+β0

y=η+ϵϵ∼N(0,σ2)

In this formulation, η is the systematic component of the model and ε is the random component. Generalised linear models (GLMs)[2] allow us to extend this formulation to problems where the distribution on the targets is not Gaussian but some other distribution (typically a distribution in the exponential family). In this case, we can write the generalised regression problem, combining the coefficients and bias for more compact notation, as:

η=β⊤x,β=[β^,β0],x=[x^,1]

E[y]=μ=g−1(η)

where g(·) is the link function that allows us to move from natural parameters η to mean parameters μ. If the inverse link function used in the definition of μ above were the logistic sigmoid, then the mean parameters correspond to the probabilities of y being a 1 or 0 under the Bernoulli distribution.

There are many link functions that allow us to make other distributional assumptions for the target (response) y. In deep learning, the link function is referred to as the activation function and I list in the table below the names for these functions used in the two fields. From this table we can see that many of the popular approaches for specifying neural networks that have counterparts in statistics and related literatures under (sometimes) very different names, such multinomial regression in statistics and softmax classification in deep learning, or rectifier in deep learning and tobit models is statistics.

Target Type	Regression	Link	Inv link	Activation
Real	Linear	Identity	Identity
Binary	Logistic	Logit logμ1−μ	Sigmoid σ 11+exp(−η)	Sigmoid
Binary	Probit	Inv Gauss CDF Φ−1(μ)	Gauss CDF Φ(η)	Probit
Binary	Gumbel	Compl. log-log log(−log(μ))	Gumbel CDF e−e−x
Binary	Logistic		Hyperbolic Tangent tanh(η)	Tanh
Categorical	Multinomial		Multin. Logit ηi∑jηj	Softmax
Counts	Poisson	log(μ)	exp(ν)
Counts	Poisson	(√μ)	ν2
Non-neg.	Gamma	Reciprocal 1μ	1ν
Sparse	Tobit		max max(0;ν)	ReLU
Ordered	Ordinal		Cum. Logit σ(ϕk−η)

Recursive Generalised Linear Models

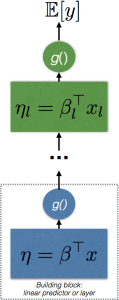
Constructing a recursive GLM or deep deep feedforward neural network using the linear predictor as the basic building block.

GLMS have a simple form: they use a linear combination of the input using weights β, and pass this result through a simple non-linear function. In deep learning, this basic building block is called a layer. It is easy to see that such a building block can be easily repeated to form more complex, hierarchical and non-linear regression functions. This recursive application of the basic regression building block is why models in deep learning are described as having multiple layers and are described as deep.

If an arbitrary regression function h, for layer l, with linear predictorη, and inverse link or activation function f, is specified as:

hl(x)=fl(ηl)

then we can easily specify a recursive GLM by iteratively applying or composing this basic building block:

E[y]=μL=hL∘…∘h1∘ho(x)

This composition is exactly the specification of an L-layer deep neural network model. There is no mystery in such a construction (and hence in feedforward neural networks) and the utility of such a model is easy to see, since it allows us to extend the power of our regressors far beyond what is possible using only linear predictors.

This form also shows that recursive GLMs and neural networks are one way of performing basis function regression. What such a formulation adds is a specific mechanism by which to specify the basis functions: by application of recursive linear predictors.

Learning and Estimation

Given the specification of these models, what remains is an approach for training them, i.e. estimation of the regression parameters β for every layer. This is where deep learning has provided a great deal of insight and has shown how such models can be scaled to very high-dimensional inputs and on very large data sets.

A natural approach is to use the negative log-probability as the loss function and maximum likelihood estimation [3]:

L=−logp(y|μL)

where if using the Gaussian distribution as the likelihood function we obtain the squared loss, or if using the Bernoulli distribution we obtain the cross entropy loss. Estimation or learning in deep neural networks corresponds directly to maximum likelihood estimation in recursive GLMs. We can now solve for the regression parameters by computing gradients w.r.t. the parameters and updating using gradient descent. Deep learning methods now always train such models using stochastic approximation (usingstochastic gradient descent), using automated tools for computing the chain rule for derivatives throughout the model (i.e. back-propagation), and perform the computation on powerful distributed systems and GPUs. This allows such a model to be scaled to millions of data points and to very large models with potentially millions of parameters [4].

From the maximum likelihood theory, we know that such estimators can be prone to overfitting and this can be reduced by incorporating model regularisation, either using approaches such as penalised regression and shrinkage, or through Bayesian regression. The importance of regularisation has also been recognised in deep learning and further exchange here could be beneficial.

Summary

Deep feedforward neural networks have a direct correspondence to recursive generalised linear models and basis function regression in statistics -- which is an insight that is useful in demystifying deep networks and an interpretation that does not rely on analogies to sequential processing in the brain. The training procedure is an application of (regularised) maximum likelihood estimation, for which we now have a large set of tools that allow us to apply these models to very large-scale, real-world systems. A statistical perspective on deep learning points to a broad set of knowledge that can be exchanged between the two fields, with the potential for further advances in efficiency and understanding of these regression problems. It is thus one I believe we all benefit from by keeping in mind. There are other viewpoints such as the connection to graphical models, or for recurrent networks,to dynamical systems, which I hope to think through in the future.

Some References

[1]	Christopher M Bishop, Neural networks for pattern recognition, , 1995
[2]	Peter McCullagh, John A Nelder, Generalized linear models., , 1989
[3]	Peter J Bickel, Kjell A Doksum, Mathematical Statistics, volume I, , 2001
[4]	Leon Bottou, Stochastic Gradient Descent Tricks, Neural Networks: Tricks of the Trade, 2012