poj 2007 凸包构造和极角排序输出（模板题）

Scrambled Polygon

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 10841		Accepted: 5085

Description

A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex. 

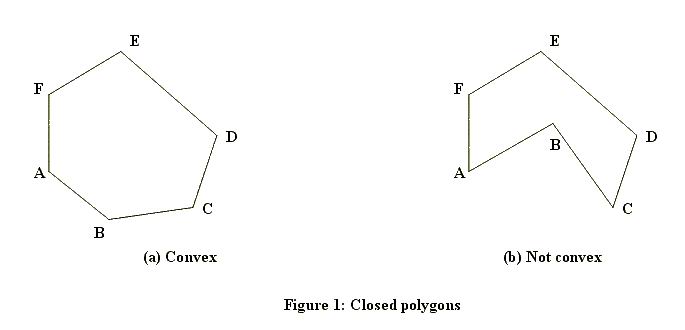
A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".) 

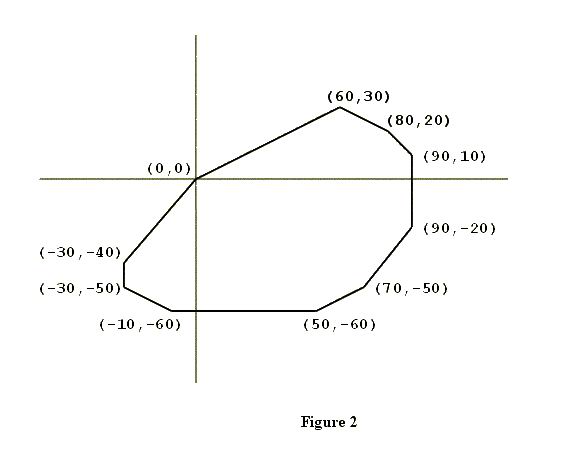
The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem. 

The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0). 

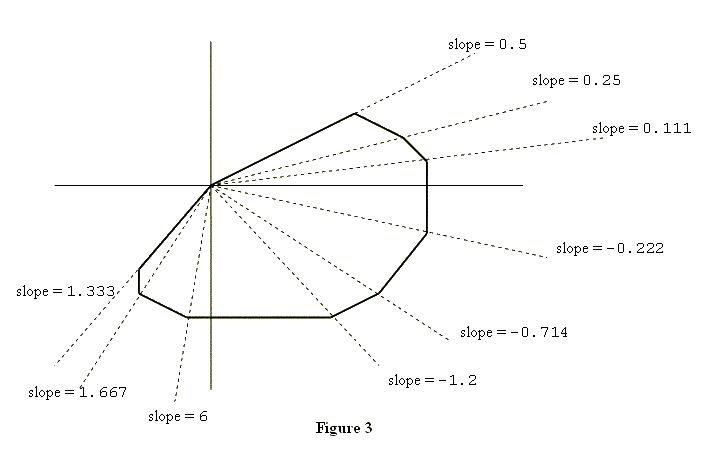
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point. 
 

Input

The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear.

Output

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below.

Sample Input

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

Sample Output

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)

#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdio>
using namespace std;

const int MAXN =55;
const double PI= acos(-1.0);
//精度
double eps=1e-8;
//避免出现-0.00情况，可以在最后加eps
//精度比较
int sgn(double x)
{
    if(fabs(x)<=eps)return 0;
    if(x<0)return -1;
    return 1;
}

//点的封装
struct Point
{
    double x,y;
    Point (){}
    //赋值
    Point (double _x,double _y)
    {
        x=_x;
        y=_y;
    }
    //点相减
    Point operator -(const Point &b)const
    {
    return Point (x-b.x,y-b.y);
    }
    //点积
    double  operator *(const Point &b)const
    {
        return x*b.x+y*b.y;
    }
    //叉积
    double operator ^(const  Point  &b)const
    {
        return x*b.y-y*b.x;
    }
} ;

//线的封装
struct Line
{
    Point s,e;
    Line (){}
    Line (Point _s,Point _e)
    {
        s=_s;
        e=_e;
    }
//平行和重合判断 相交输出交点
//直线相交和重合判断，不是线段，
    Point operator &(const Line &b)const{
    Point res=b.s;
    if(sgn((e-s)^(b.e-b.s))==0)
    {
        if(sgn((e-s)^(e-b.e))==0)
        {
            //重合
            return Point(0,0);
        }
        else
            {
               //平行
                return Point(0,0);
            }
    }
    double t=((e-s)^(s-b.s))/((e-s)^(b.e-b.s));
    res.x+=(b.e.x-b.s.x)*t;
    res.y+=(b.e.y-b.s.y)*t;
    return res;
    }
};

//向量叉积
double xmult(Point p0,Point p1,Point p2)
{
    return (p0-p1)^(p2-p1);
}

//线段和线段非严格相交，相交时true
//此处是线段
bool seg_seg(Line l1,Line l2)
{
    return sgn(xmult(l1.s,l2.s,l2.e)*xmult(l1.e,l2.s,l2.e))<=0&&sgn(xmult(l2.s,l1.s,l1.e)*xmult(l2.e,l1.s,l1.e))<=0;
}

//两点之间的距离
double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}

//极角排序;对100个点进行极角排序
int pos;//极点下标
Point p[MAXN];
int Stack[MAXN],top;
bool cmp(Point a,Point b)
{
    double tmp=sgn((a-p[pos])^(b-p[pos]));//按照逆时针方向进行排序
    if(tmp==0)return dist(a,p[pos])<dist(b,p[pos]);
    if(tmp<0)return false ;
    return true;
}
void Graham(int n)
{
    Point p0;
    int k=0;
    p0=p[0];
    for(int i=1;i<n;i++)//找到最左下边的点
    {
        if(p0.y>p[i].y||(sgn(p0.y-p[i].y))==0&&p0.x>p[i].x)
        {
            p0=p[i];
            k=i;
        }
    }
    swap(p[k],p[0]);
    sort(p+1,p+n,cmp);
    if(n==1)
    {
        top=2;
        Stack[0]=0;
        return ;
    }
    if(n==2)
    {
        top=2;
        Stack[0]=0;
        Stack[1]=1;
        return ;
    }
    Stack[0]=0;Stack[1]=1;
    top=2;
    for(int i=2;i<n;i++)
    {
        while(top>1&&sgn((p[Stack[top-1]]-p[Stack[top-2]])^(p[i]-p[Stack[top-2]]))<=0)
            top--;
        Stack[top++]=i;
    }
}

int main ()
{
    int t=0;
    while(~scanf("%lf%lf",&p[t].x,&p[t].y))
        t++;
    Graham(t);
    for(int i=0;i<t;i++)
    {
        if(p[i].x==0&&p[i].y==0)
        {
            swap(p[i],p[0]);
            break;
        }
    }
    sort(p,p+t,cmp);
    for(int i=0;i<t;i++)
    printf("(%.f,%.f)\n",p[i].x,p[i].y);
    return 0;
}

极角排序：

根据逆时针顺序进行排序