深度优先遍历（DFS）（转）

优先搜索(DFS, Depth First Search)是一个针对图和树的遍历算法。早在19世纪就被用于解决迷宫问题。

对于下面的树而言，DFS方法首先从根节点1开始，其搜索节点顺序是1,2,3,4,5,6,7,8（假定左分枝和右分枝中优先选择左分枝）。

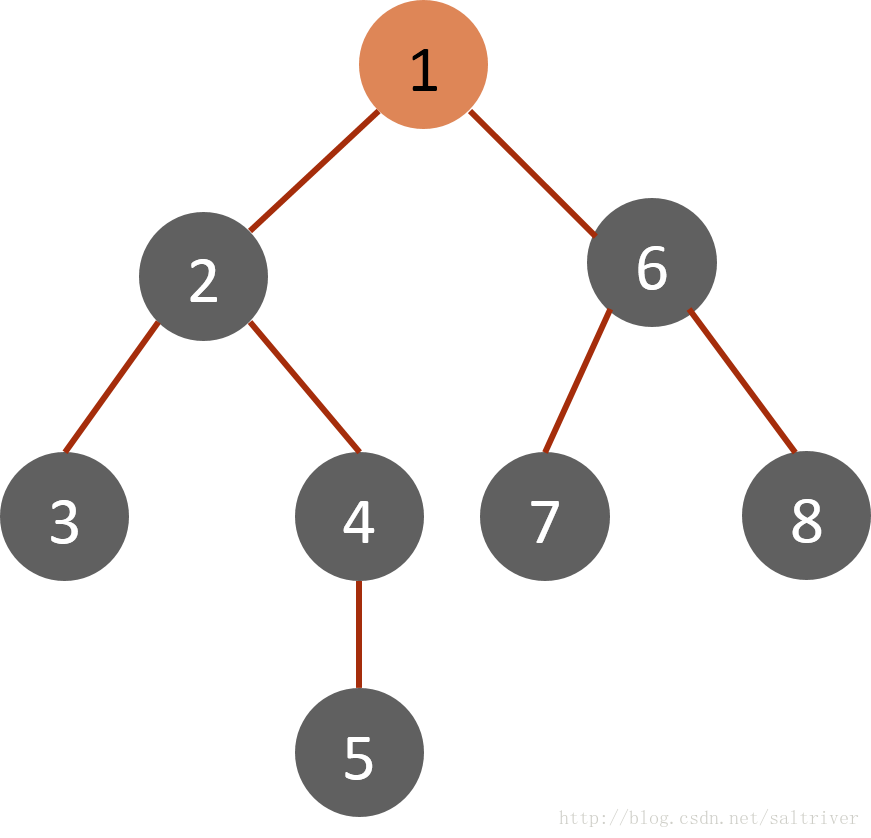
DFS的实现方式相比于BFS应该说大同小异，只是把queue换成了stack而已，stack具有后进先出LIFO(Last Input First Output)的特性，

DFS的操作步骤如下：
1、把起始点放入stack；
2、重复下述3步骤，直到stack为空为止：

a、从stack中访问栈顶的点；

b、找出与此点邻接的且尚未遍历的点，进行标记，然后全部放入stack中；

c、如果此点没有尚未遍历的邻接点，则将此点从stack中弹出。

下面结合一个图(graph)的实例，说明DFS的工作过程和原理： 

（1）将起始节点1放入栈stack中，标记为已遍历。

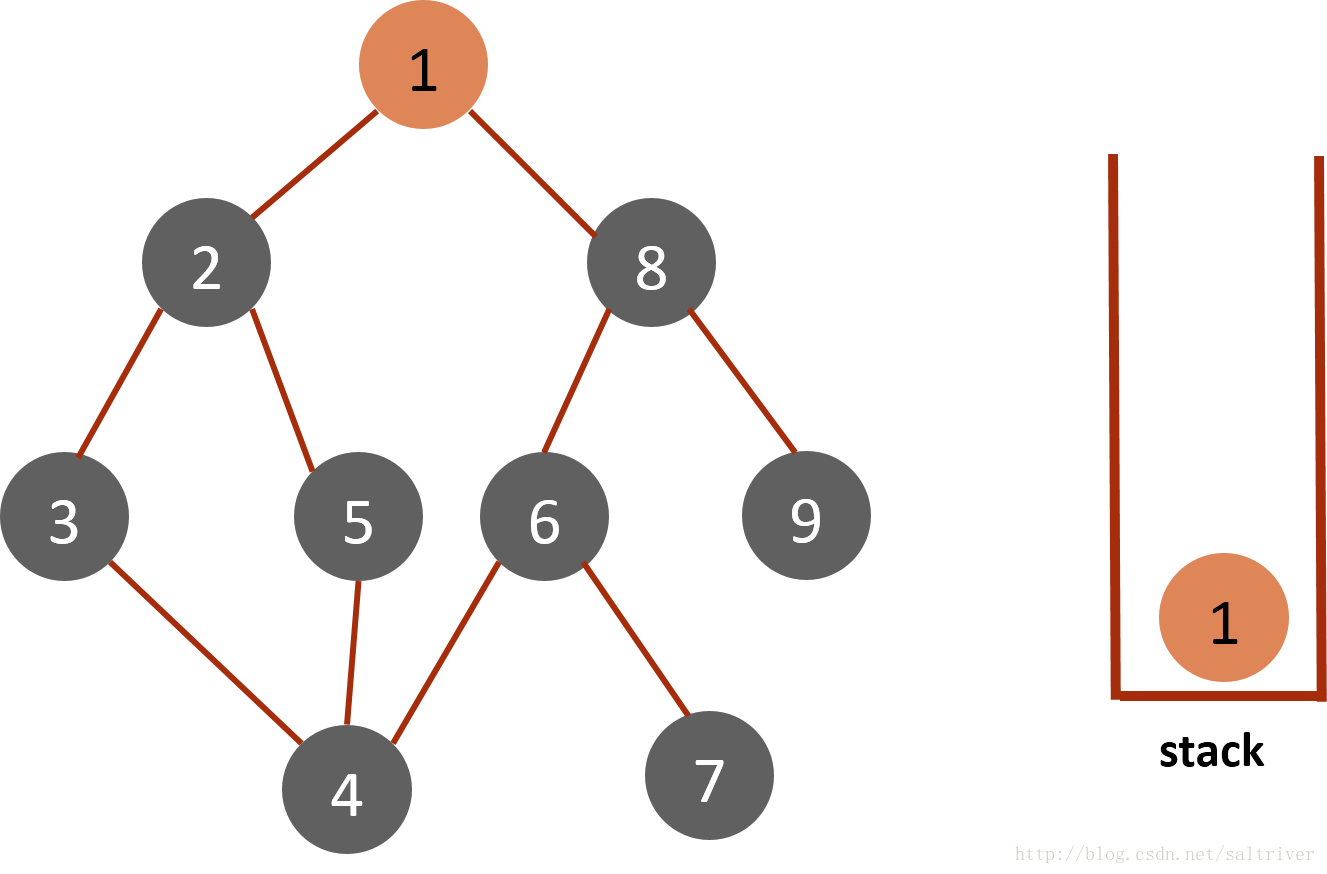
（2）从stack中访问栈顶的节点1，找出与节点1邻接的节点，有2,9两个节点，我们可以选择其中任何一个，选择规则可以人为设定，这里假设按照节点数字顺序由小到大选择，选中的是2，标记为已遍历，然后放入stack中。

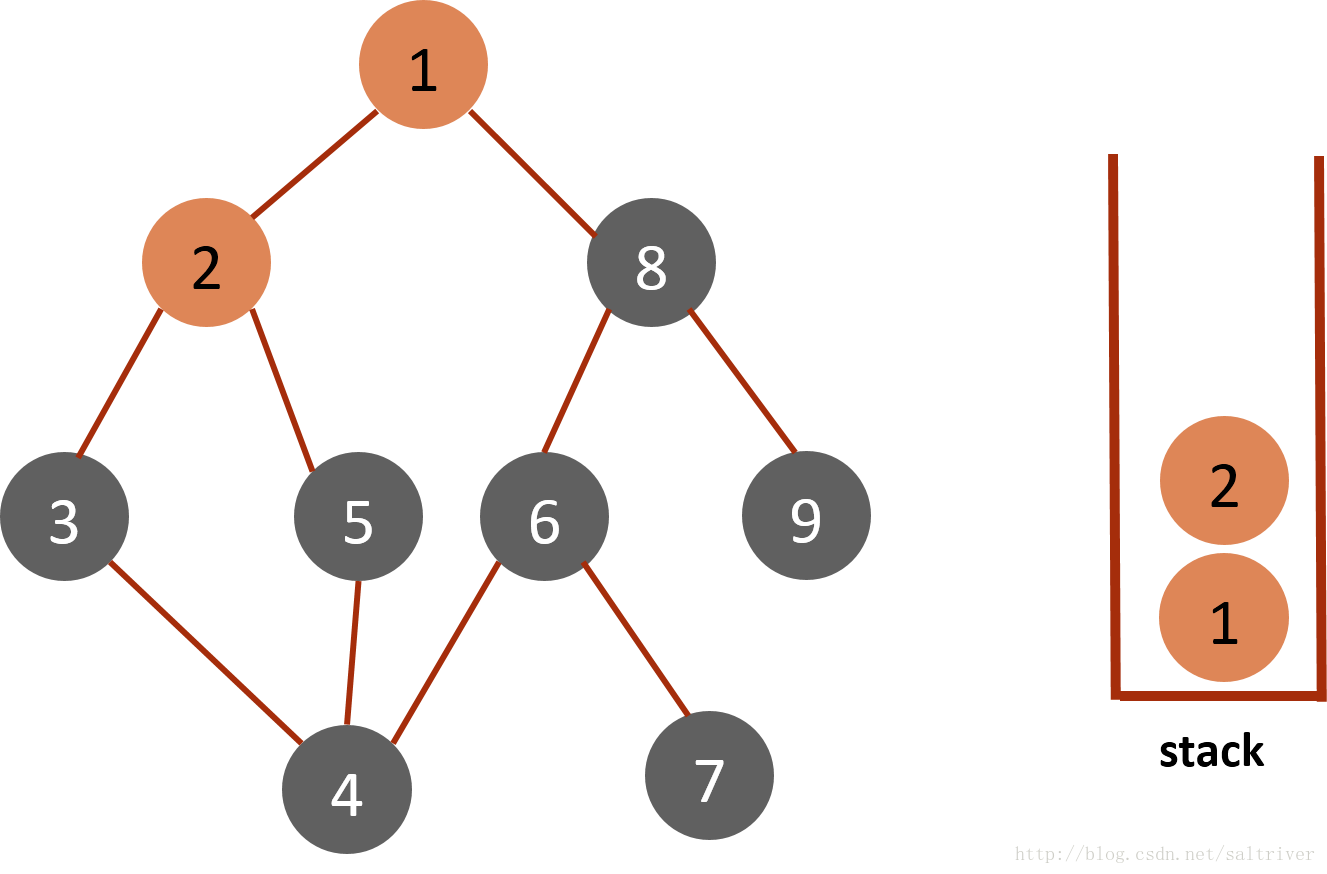
（3）从stack中取出栈顶的节点2，找出与节点2邻接的节点，有1,3,5三个节点，节点1已遍历过，排除；3,5中按照预定的规则选中的是3，标记为已遍历，然后放入stack中。

（4）从stack中取出栈顶的节点3，找出与节点3邻接的节点，有2,4两个节点，节点2已遍历过，排除；选中的是节点4，标记为已遍历，然后放入stack中。

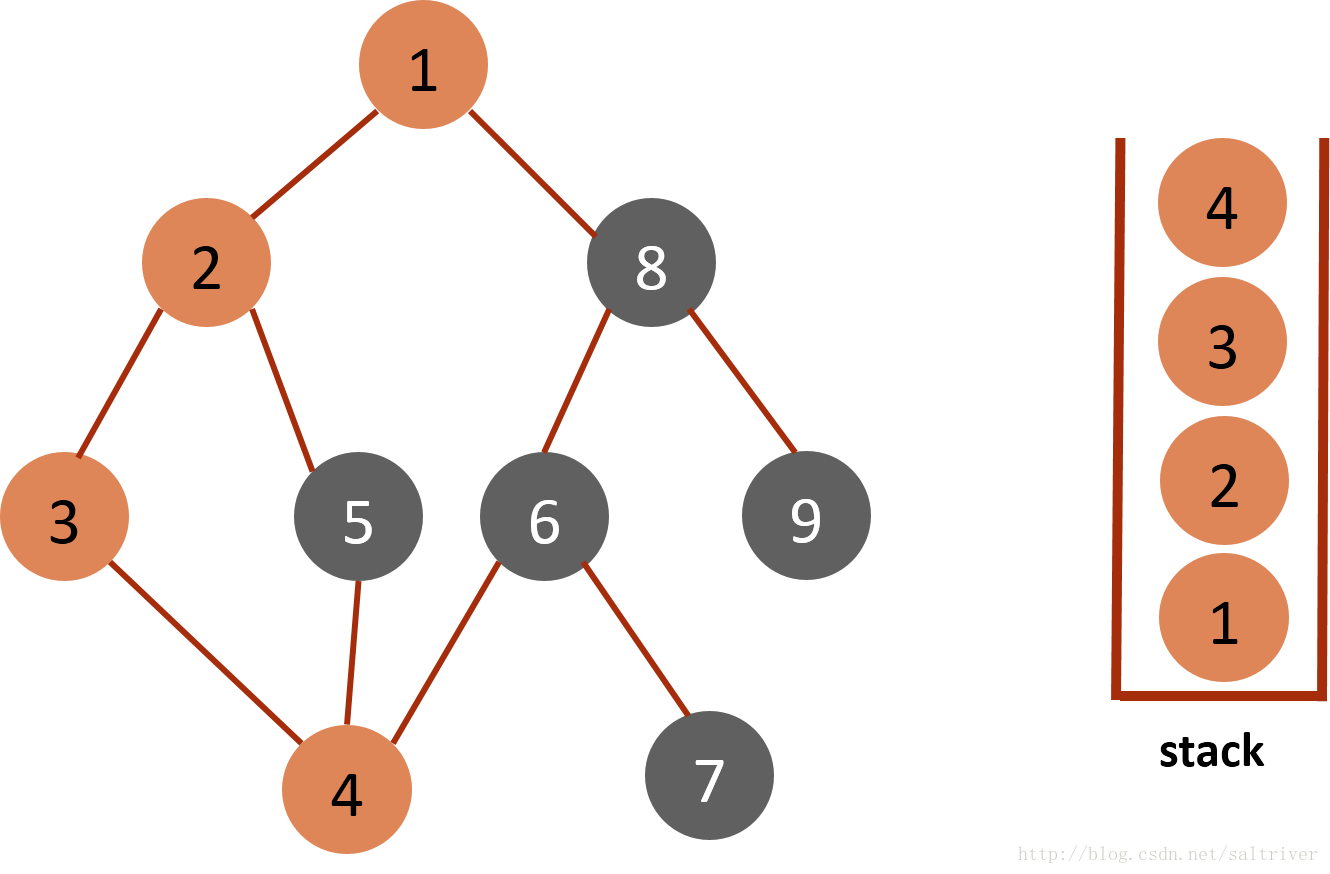
（5）从stack中取出栈顶的节点4，找出与节点4邻接的节点，有3,5,6三个节点，节点3已遍历过，排除；选中的是节点5，标记为已遍历，然后放入stack中。

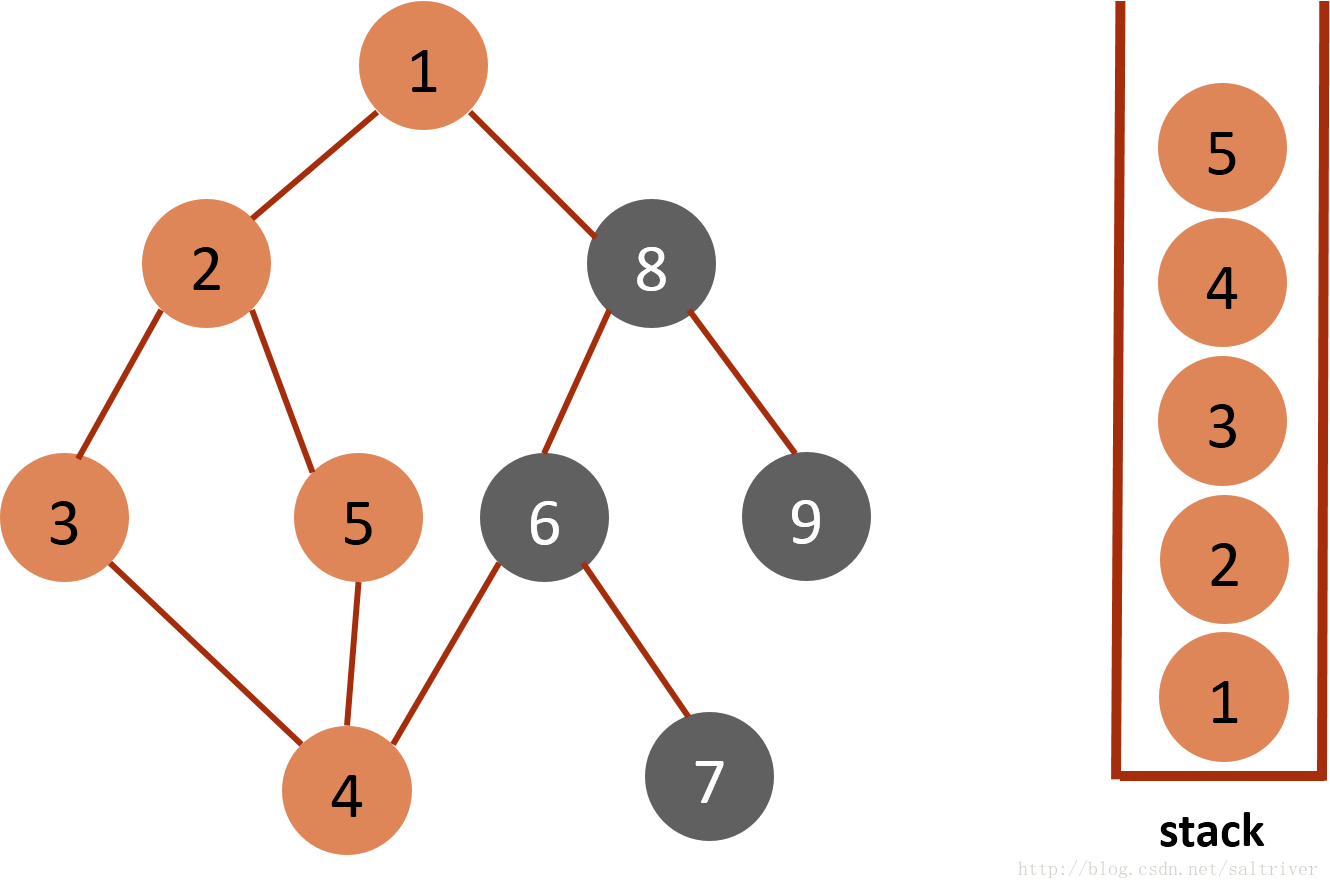
（6）从stack中取出栈顶的节点5，找出与节点5邻接的节点，有2,4两个节点，节点2,4都已遍历过，因此节点5没有尚未遍历的邻接点，则将此点从stack中弹出。

（7）当前stack栈顶的节点是4，找出与节点4邻接的节点，有3,5,6三个节点，节点3,5都已遍历过，排除；选中的是节点6，标记为已遍历，然后放入stack中。

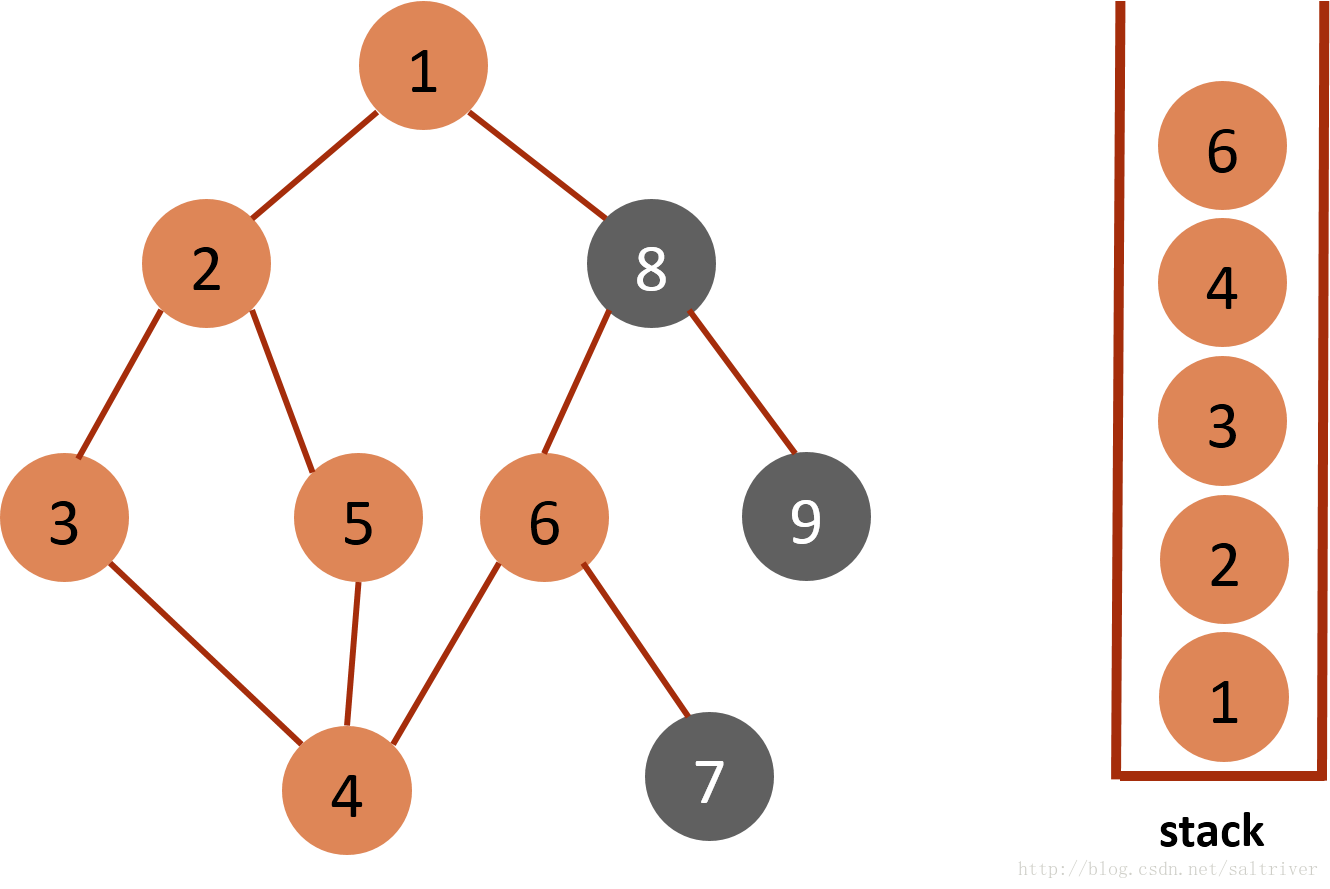
（8）当前stack栈顶的节点是6，找出与节点6邻接的节点，有4,7,8三个节点，4已遍历，按照规则选中的是7，标记为已遍历，然后放入stack中。

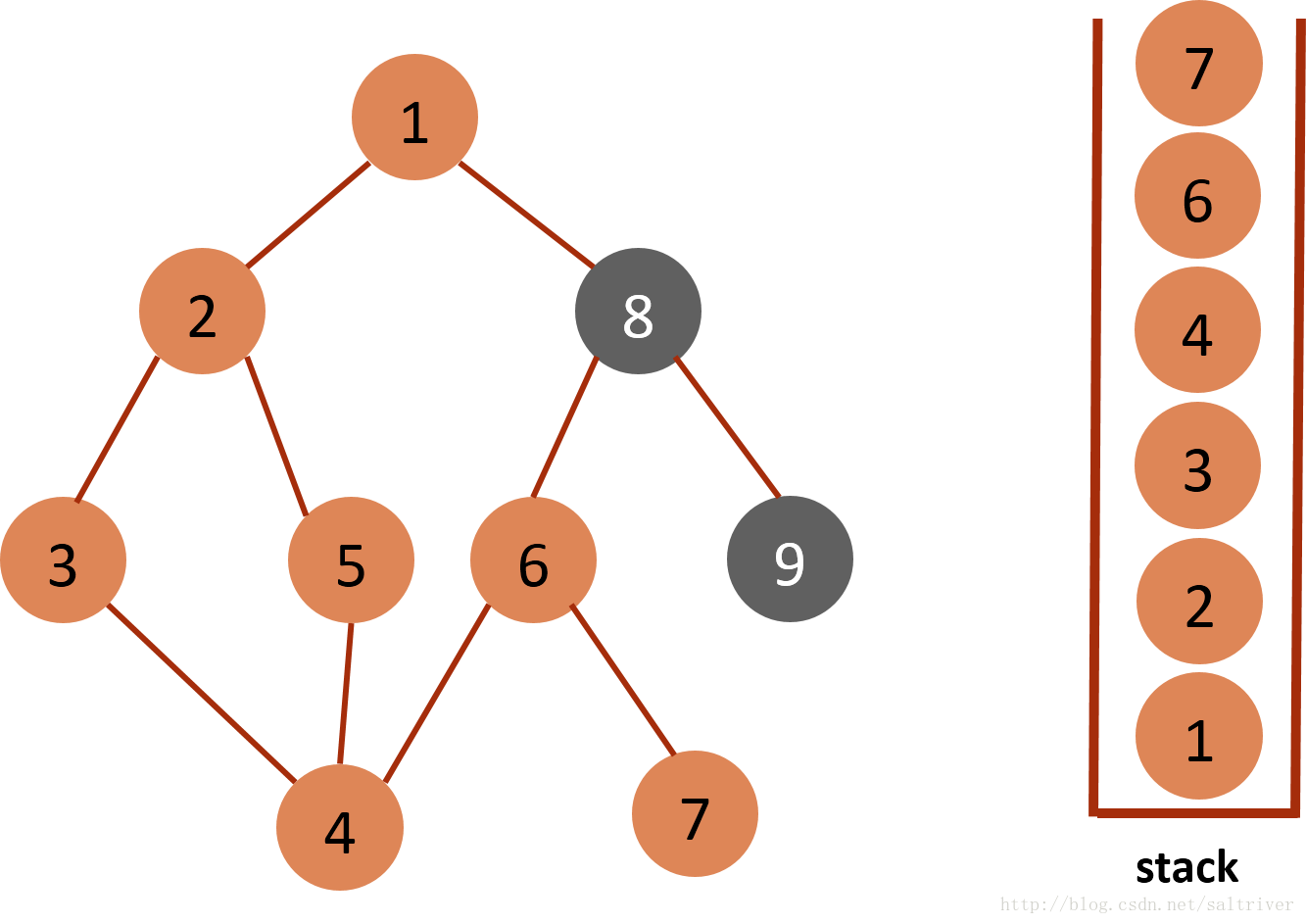
（9）当前stack栈顶的节点是7，找出与节点7邻接的节点，只有节点6，已遍历过，因此没有尚未遍历的邻接点，将节点7从stack中弹出。

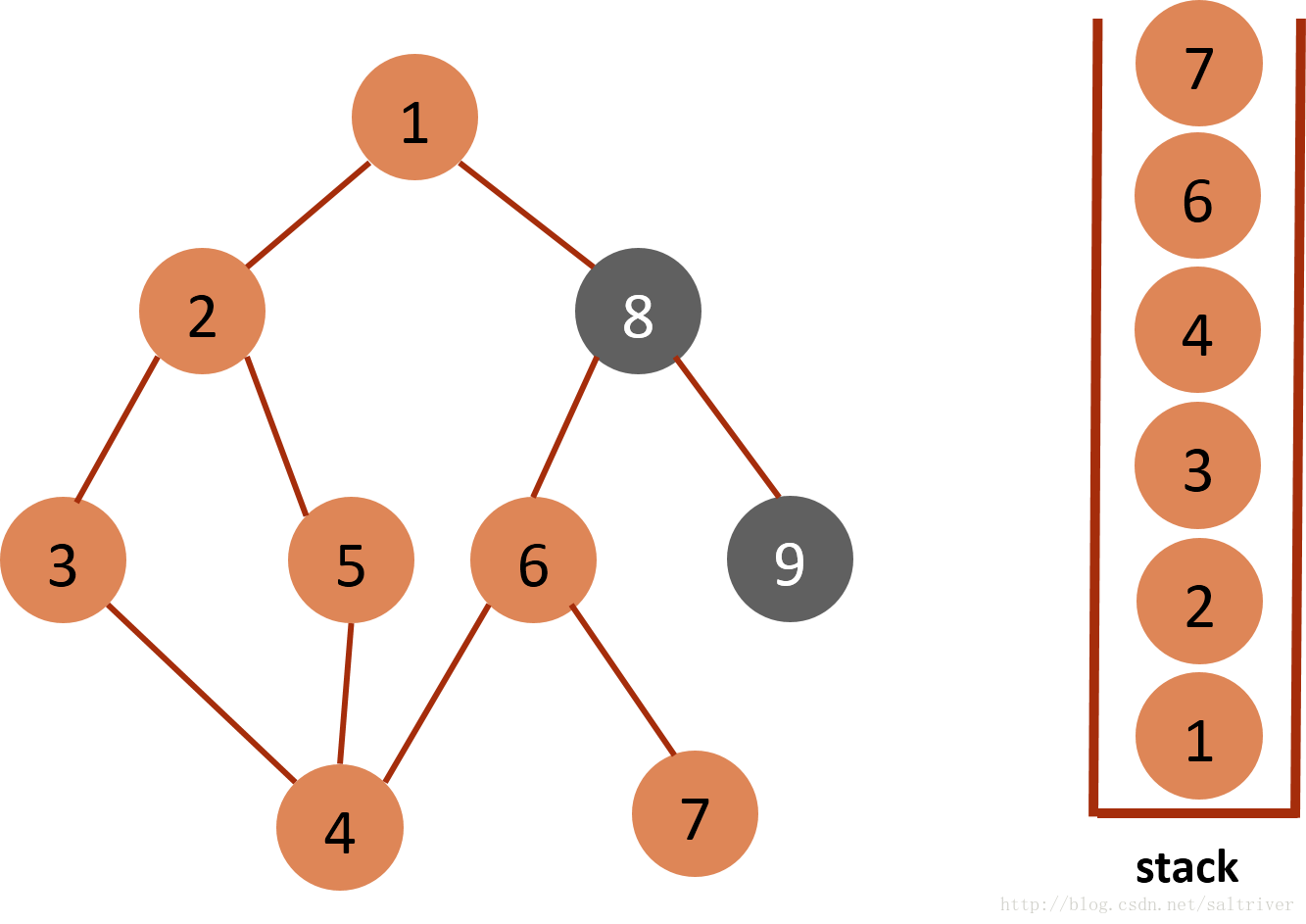
（10）当前stack栈顶的节点是6，找出与节点6邻接的节点，有节点7,8，7已遍历过，因此将节点8放入stack中。

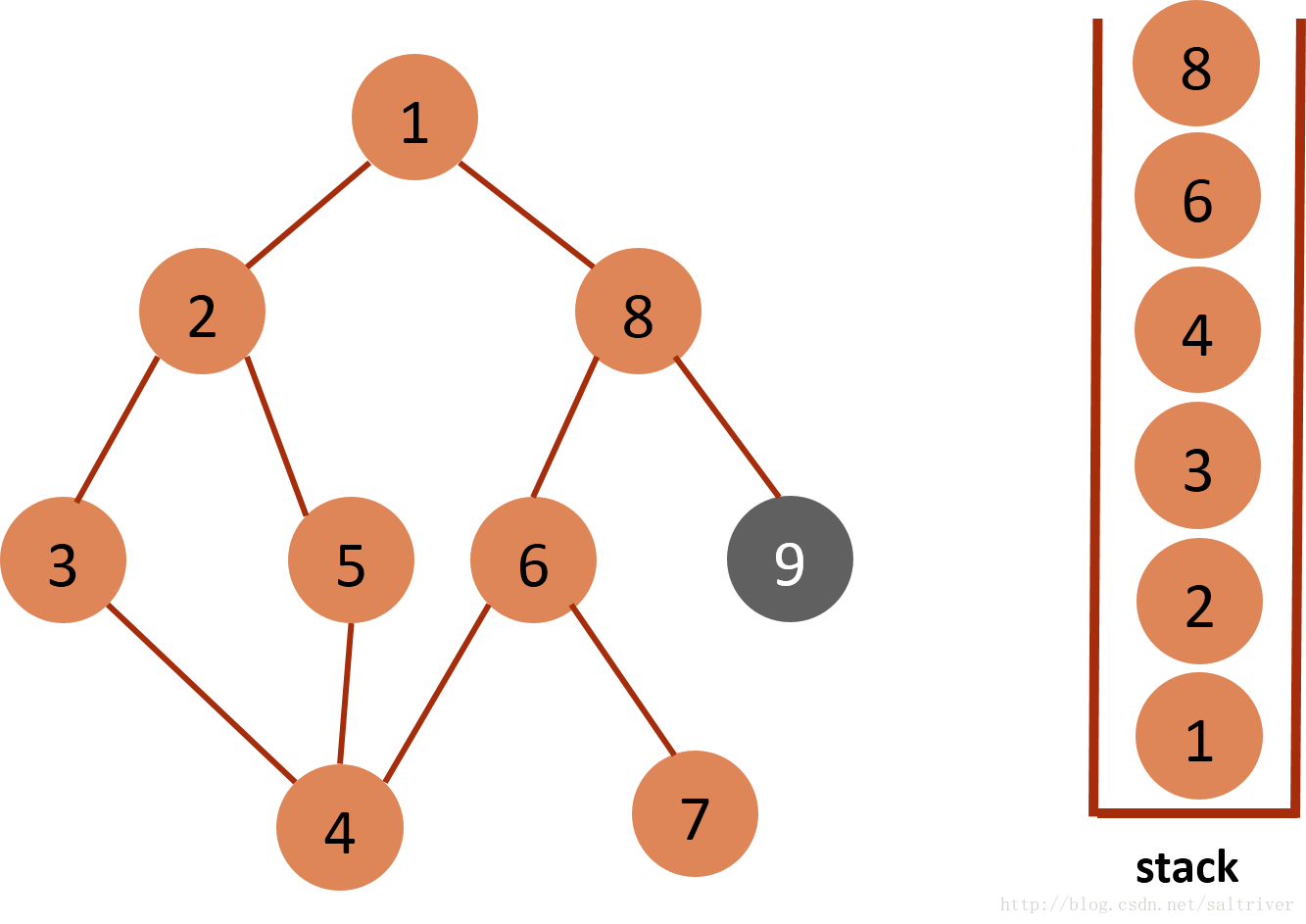
（11）当前stack栈顶的节点是8，找出与节点8邻接的节点，有节点1,6,9，1,6已遍历过，因此将节点9放入stack中。

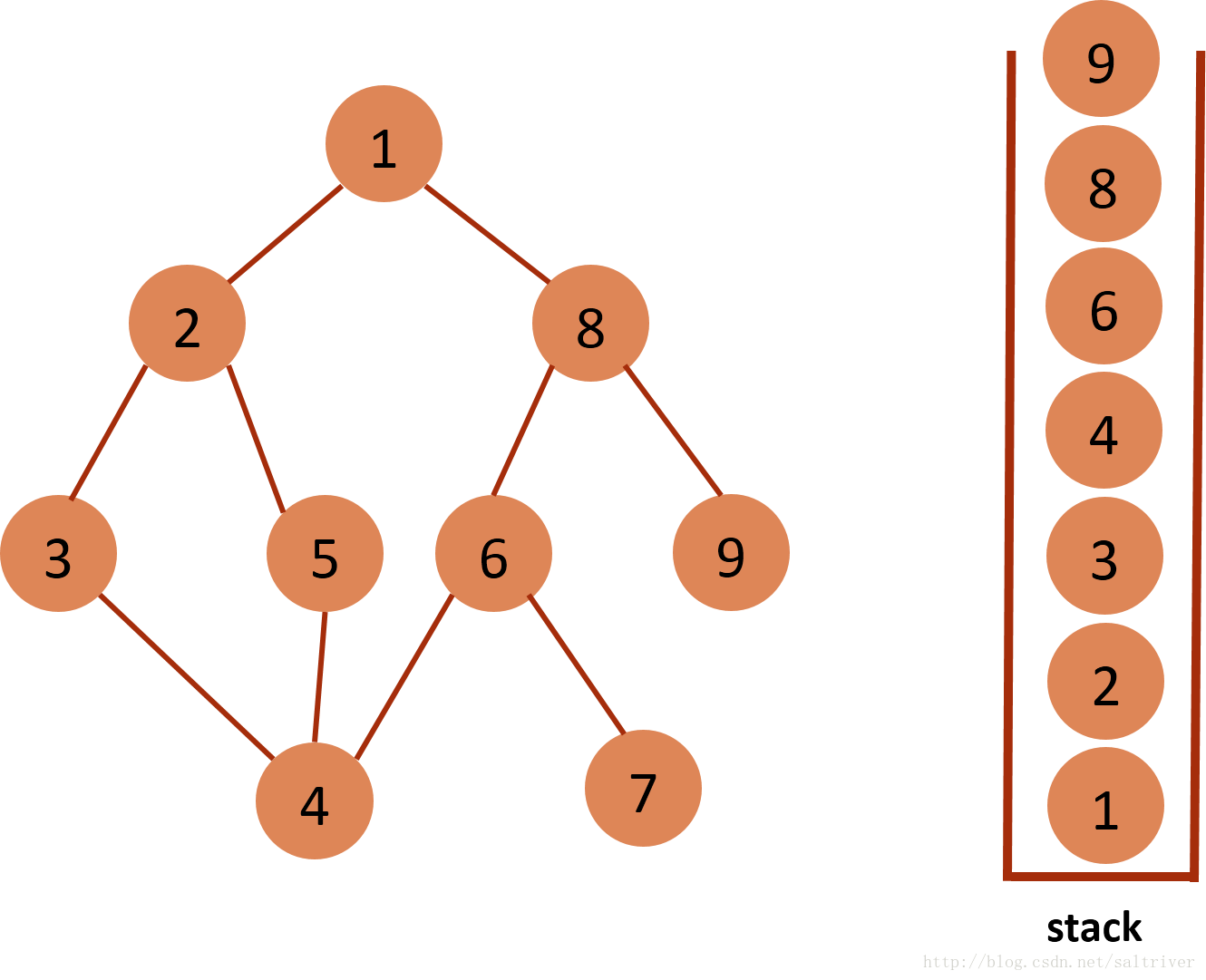
（12）当前stack栈顶的节点是9，没有尚未遍历的邻接点，将节点9弹出，依次类推，栈中剩余节点8,6,4,3,2,1都没有尚未遍历的邻接点，都将弹出，最后栈为空。

（13）DFS遍历完成。
---------------------
作者：saltriver
来源：CSDN
原文：https://blog.csdn.net/saltriver/article/details/54429068
版权声明：本文为博主原创文章，转载请附上博文链接！

应用连接：https://blog.csdn.net/raphealguo/article/details/7560918