静态牵拉一般在运动后进行，可以有效的提高肌肉的柔韧性和关节的灵活性，预防和缓解疼痛。 每个动作达到自己活动范围的最大，有牵拉感即说明有效，静态保持至少30秒，切勿震荡，进行2组。

1 大腿前群牵拉

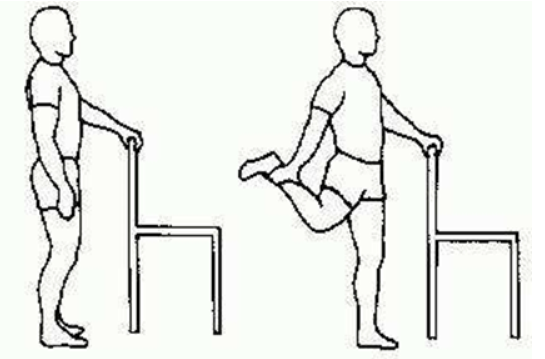
2 大腿后群牵拉

3 大腿内侧牵拉

4 大腿外侧牵拉

5 小腿牵拉

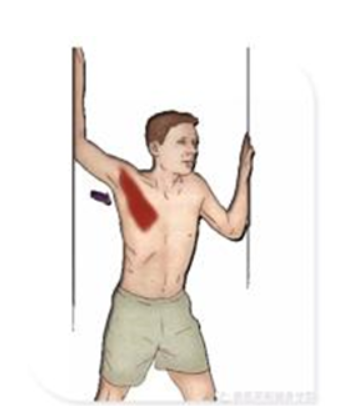
6 胸肌前拉

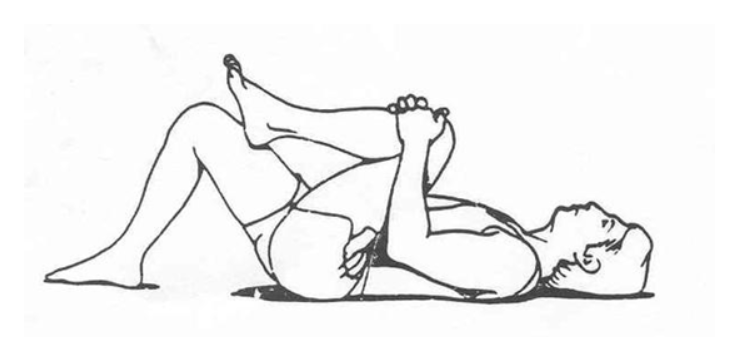
7 臀肌牵拉

参考资料

[1]知乎，李明威的回答

【EverydaySport】健身笔记——静态牵拉的更多相关文章

  1. 【EverydaySport】健身笔记——动态牵拉

    动态牵拉,包含了动态和牵拉两个概念.动态牵拉要求牵拉的过程要伴随着走路,即行进中牵拉,动态牵拉不仅可以使得肌肉得到延展,还可以激活肌肉协同工作,发展协调性.灵活性.进行动态牵拉时每个动作要进行5~10 ...

  2. Uep的静态下拉和动态下拉建立

    uep的静态下拉和动态下拉的建立极其省事,下面介绍静态下拉的建立 静态下拉 第一步:点击增加,输入信息 第二步: 第三步:保存 第四部: 静态下拉就建立完毕了 下面介绍动态下啦建立,动态下拉更简单 动 ...

  3. 【EverydaySport】健身笔记——背部训练

    背部训练大致可以分为两种. 1 下拉式动作 躯干纵向上下位移的动作 典型代表 这样的下拉类动作 针对的是背阔肌 也就是两边像翅膀一样的部分 2 垂直于躯干的方向作用 向内拉 主要针对的是,背部的中部 ...

  4. 【EverydaySport】健身笔记——人体肌肉分解图

    正面 背面 大肌肉群:胸.背.腿大肌肉群. 建议一周锻炼一次. 小肌肉群:肩.二头肌.三头肌.小臂.小腿.腹肌小肌肉群. 可以一周安排两次. 小腿.小臂肌群属于耐受肌群可以一周安排3次. 建议初学者就 ...

  5. [Spring入门学习笔记][静态资源]

    遗留问题 在上一节课的作业中,我们一定遇到了一点问题——虽然将页面内容正确的返回给了浏览器,但是浏览器显示的样式却是不正确的,这是因为在HTML的\标签中我们这样引入了CSS资源: <link ...

  6. C语言数据结构基础学习笔记——静态查找表

    查找:在数据集合中寻找满足某种条件的数据元素的过程称为查找. 查找表:用于查找的数据集合称为查找表,一般有以下操作:①查找是否在表中:②查找属性:③进行操作. 查找表又分为: ①静态查找表:只可以进行 ...

  7. QTP 自动化测试桌面程序--笔记（下拉选择、右键菜单、在控件仓库中查找对应的控件）

    0 在收集窗口控件信息时-最好将可输入的文字去掉,不然控件的名称按输入的文字标记 1 编辑时录制脚本-默认按当前显示的填入的数据标记控件 可以使用 tool-spy-查看控件的x,y 坐标,按坐标在学 ...

  8. C#学习笔记----静态字段和静态方法

    1.使用关键字 static 修饰的字段或方法成为静态字段和静态方法,如 public static int num = 1;2.静态字段属于类,并为类所用.而非静态字段属于对象,只能被特定的对象专有 ...

  9. 08-Node.js学习笔记-静态资源访问

    静态资源 服务器端不需要处理,可以直接响应给客户端的资源就是静态资源,例如css,javaScript,image文件 动态资源 相同的请求地址不同的响应资源,这种资源就是动态资源 http://ww ...

随机推荐

  1. 进程&线程间通信方式总结

    一.进程间的通信方式 # 管道( pipe ):管道是一种半双工的通信方式,数据只能单向流动,而且只能在具有亲缘关系的进程间使用.进程的亲缘关系通常是指父子进程关系. # 有名管道 (namedpip ...

  2. WPF布局间的切换方法

    效果图,两种效果间的切换

  3. POJ2318：TOYS——题解

    http://poj.org/problem?id=2318 题目大意:给一个大矩形,分成n+1份,求落在每一份的点的数量. —————————————————— 首先叉积可以判断一个点在边界的左边还 ...

  4. BZOJ3435 & 洛谷3920 & UOJ55：[WC2014]紫荆花之恋

    https://www.lydsy.com/JudgeOnline/problem.php?id=3435 https://www.luogu.org/problemnew/show/P3920 ht ...

  5. ZOJ2314：Reactor Cooling——题解

    http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1314 题目大意:无源汇上下界网络流,问每个管子走多少流量才能满足所有管子的下界 ...

  6. LOJ6303：水题——题解

    https://loj.ac/problem/6303 题目来自LOJ. 就记一个公式,设f(n,k)为n!里分解得到的k(k为质数)的个数,则f(n,k)=f(n/k,k)+n/k. 证明很好证,显 ...

  7. [zhuan]动态链接库中的.symtab和.dynsym

    http://blog.csdn.net/beyond702/article/details/50979340 原文如下: shared library (.so) "Program Lib ...

  8. STL之三：deque用法详解

    转载于:http://blog.csdn.net/longshengguoji/article/details/8519812 deque函数: deque容器为一个给定类型的元素进行线性处理,像向量 ...

  9. Android提示框与通知的使用

    1.通知 Android 3.0以前使用的方法 NotificationManager nm = (NotificationManager) getSystemService(NOTIFICATION ...

  10. [mysql][【优化集合】mysql数据库优化集合

    三个层面: 1.系统层面 2.mysql配置参数 3.sql语句优化 =========================================================== 一.系统层 ...