算法之暴力破解和kmp算法 判断A字符串是否包含B字符串

我们都知道java中有封装好的方法，用来比较A字符串是否包含B字符串

如下代码，contains,用法是 str1.contains(str2), 这个布尔型返回，存在返回true，不存在返回false

还有indexOf，用法和contains一致，返回值是int，存在则返回对应的位置，注意位置从0开始的，不存在返回-1

public class Test {

    public static void main(String[] args) {

        String source = "abacaabacabacabaabb";
        String pattern = "abacab";
        System.out.println(source.contains(pattern) );   //true
        System.out.println(source.indexOf(pattern) );   //
    }
}

这两个方法的具体实现，是在java.lang包中，最终类String下

    public boolean contains(CharSequence s) {
        return indexOf(s.toString()) > -1;
    }

contains其实调用了indexOf

    public int indexOf(String str) {
        return indexOf(str, 0);
    }

    public int indexOf(String str, int fromIndex) {
        return indexOf(value, 0, value.length,
                str.value, 0, str.value.length, fromIndex);
    }

static int indexOf(char[] source, int sourceOffset, int sourceCount,
            char[] target, int targetOffset, int targetCount,
            int fromIndex) {
        if (fromIndex >= sourceCount) {
            return (targetCount == 0 ? sourceCount : -1);
        }
        if (fromIndex < 0) {
            fromIndex = 0;
        }
        if (targetCount == 0) {
            return fromIndex;
        }

        char first = target[targetOffset];
        int max = sourceOffset + (sourceCount - targetCount);

        for (int i = sourceOffset + fromIndex; i <= max; i++) {
            /* Look for first character. */
            if (source[i] != first) {
                while (++i <= max && source[i] != first);
            }

            /* Found first character, now look at the rest of v2 */
            if (i <= max) {
                int j = i + 1;
                int end = j + targetCount - 1;
                for (int k = targetOffset + 1; j < end && source[j]
                        == target[k]; j++, k++);

                if (j == end) {
                    /* Found whole string. */
                    return i - sourceOffset;
                }
            }
        }
        return -1;
    }

如果你没有去看java中自带的实现，要你自己写方法实现呢

这就涉及到了算法：算法就是你的思路=======

第一步： 先构思一下思路，我要怎么去比较；一般人的思路是：

我拿后者的第一个字符，去看前者中是否含有，如果米有，一定不匹配；

我拿后者的第一个字符，去看前者中是否含有，如果前者中含有，继续查看，第二个字符是否和长串中接下来的一个字符相等

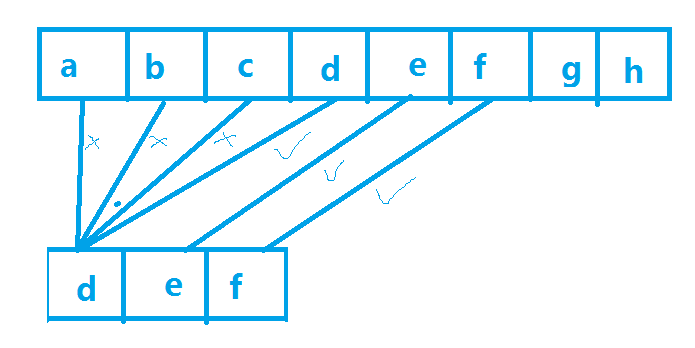
相等，继续向下匹配(如下图一)

不相等，重新用后者的第一个字符再和长字符串接下来一位进行比较

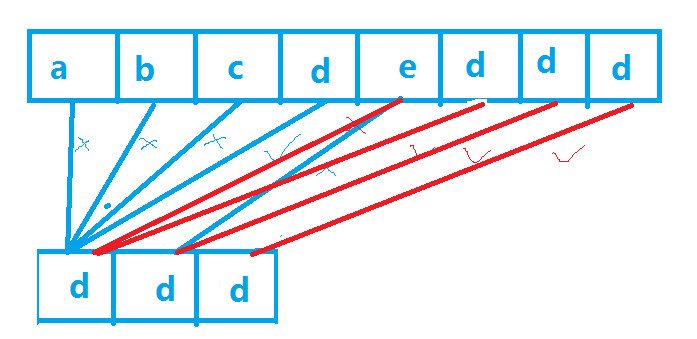
何谓接下来一位呢【假设abcdefgh和ddd，第一次比配到长字符串的第四位相等，第二次和长字符串的第5位开始比较，如下图二】

public class Force {

    /**
     * 暴力匹配
     * 　时间复杂度为O(n*m)；n为主串长度，m为模式串长度
     　　        算法的基本思想：
     　　　　　　从主串的起始位置（或指定位置）开始与模式串的第一个字符比较，若相等，则继续逐个比较后续字符；
     否则从主串的下一个字符再重新和模式串的字符比较。
     依次类推，直到模式串成功匹配，返回主串中第一次出现模式串字符的位置，或者模式串匹配不成功，返回不成功，实际中可将返回值设置为int，不成功返回-1，成功返回0；
     * @param source
     * @param pattern
     * @return
     */
    public static String bruteForceStringMatch(String source, String pattern) {
        int slen = source.length();
        int plen = pattern.length();
        char[] s = source.toCharArray();
        char[] p = pattern.toCharArray();
        int i = 0;
        int j = 0;

        if (slen < plen)
            return "你瞧瞧主串长度小于模式串，怎么可能啊，匹配失败"; // 如果主串长度小于模式串，直接返回-1，匹配失败
        else {
            while (i < slen && j < plen) {
                if (s[i] == p[j]) // 如果i,j位置上的字符匹配成功就继续向后匹配
                {

                    System.out.println(i+ "的值是"+ s[i] );
                    System.out.println(j + "的值是"+ p[j]);
                    ++i;
                    ++j;

                } else {

                    System.out.println("我是else下的" + i + "的值是"+ s[i] );
                    System.out.println("我是else下的" + j + "的值是"+ p[j]);
                    i = i - (j - 1); // i回溯到主串上一次开始匹配下一个位置的地方
                    j = 0; // j重置，模式串从开始再次进行匹配
                }
            }
            if (j == plen) // 匹配成功
                return "位置是"+(i+1 - j);
            else
                return "匹配失败"; // 匹配失败
        }
    }

}

查看匹配结果：

这是暴力破解，abcdeddd和ddd，在ddd的第0位和abcdeddd的第3位匹配后，继续比较下一位，发现不匹配了，重新将ddd的第0位和

kmp的思路如下：

KMP算法
　　KMP算法是D.E.Knuth、V.R.Pratt和J.H.Morris同时发现，所以命名为KMP算法。
　　此算法可以在O(n+m)的时间数量级上完成串的模式匹配。
　　主要就是改进了暴力匹配中i回溯的操作，KMP算法中当一趟匹配过程中出现字符比较不等时，
不直接回溯i，而是利用已经得到的“部分匹配”的结果将模式串向右移动（j-next[k]）的距离。

import java.util.Arrays;

public class kmp {

    /**
     * KMP算法
     　　KMP算法是D.E.Knuth、V.R.Pratt和J.H.Morris同时发现，所以命名为KMP算法。
     　　此算法可以在O(n+m)的时间数量级上完成串的模式匹配。
     　　主要就是改进了暴力匹配中i回溯的操作，KMP算法中当一趟匹配过程中出现字符比较不等时，
     不直接回溯i，而是利用已经得到的“部分匹配”的结果将模式串向右移动（j-next[k]）的距离。

     * @param source
     * @param pattern
     * @return
     */
    public static String kmpStringMatch(String source, String pattern)
    {
        int i = 0;
        int j = 0;
        char[] s = source.toCharArray();
        char[] p = pattern.toCharArray();
        int slen = s.length;
        int plen = p.length;
        int[] next = getNext(p);

        while(i < slen && j < plen)
        {
            if(j == -1 || s[i] == p[j])
            {
                ++i;
                ++j;
            }
            else
            {
                //如果j != -1且当前字符匹配失败，则令i不变，
                //j = next[j],即让pattern模式串右移j - next[j]个单位
                j = next[j];
            }
        }

        if(j == plen)
            return "位置是"+(i+1 - j);
        else
            return "匹配失败"; // 匹配失败
    }

    /**
     * 关于next[k]数组的计算引出的两种办法，一种是递归，一种对递归优化，第一种对应的就是KMP算法，第二种就是优化的KMP算法。
     next函数值仅取决于模式串本身而和主串无关。
     有很多讲next函数值计算办法的资料，在此我想用一种直观的比较容易理解的办法来表达。
     举个栗子：现在有一个模式串abab

     模式串的各个字串　                            前缀                                               后缀                        最大公共元素长度
     a    null    null    0
     ab    a    b    0
     aba    a,ab    a,ba    1
     abab    a,ab,aba    b,ab,bab    2
     * @param p
     * @return
     */
    private static int[] getNext(char[] p)
    {
        /**
         * 已知next[j] = k, 利用递归的思想求出next[j+1]的值
         * 1.如果p[j] = p[k]，则next[j+1] = next[k] + 1;
         * 2.如果p[j] != p[k],则令k = next[k],如果此时p[j] == p[k],则next[j+1] = k+1
         * 如果不相等，则继续递归前缀索引，令k=next[k],继续判断，直至k=-1(即k=next[0])或者p[j]=p[k]为止
         */
        int plen = p.length;
        int[] next = new int[plen];
        System.out.println("next函数值：" + Arrays.toString(next));

        int k = -1;
        int j = 0;
        next[0] = -1;                //这里采用-1做标识
        while(j < plen -1)
        {
            if(k == -1 || p[j] == p[k])
            {
                ++k;
                ++j;
                next[j] = k;
            }
            else
            {
                k = next[k];
            }
        }
        System.out.println("next函数值：" + Arrays.toString(next));
        return next;
    }
}