Convex Hull | Set 1

Given a set of points in the plane. the convex hull of the set is the smallest convex polygon that contains all the points of it.

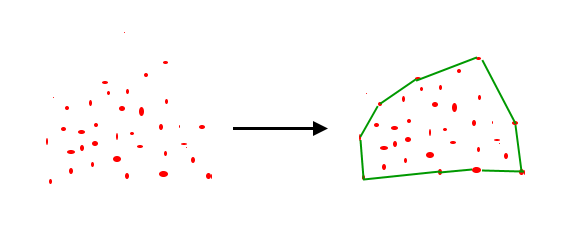
https://www.geeksforgeeks.org/convex-hull-set-1-jarviss-algorithm-or-wrapping/

Lin家

Java:

// Java program to find convex hull of a set of points. Refer
// https://www.geeksforgeeks.org/orientation-3-ordered-points/
// for explanation of orientation()
import java.util.*; 

class Point
{
    int x, y;
    Point(int x, int y){
        this.x=x;
        this.y=y;
    }
} 

class GFG { 

    // To find orientation of ordered triplet (p, q, r).
    // The function returns following values
    // 0 --> p, q and r are colinear
    // 1 --> Clockwise
    // 2 --> Counterclockwise
    public static int orientation(Point p, Point q, Point r)
    {
        int val = (q.y - p.y) * (r.x - q.x) -
                  (q.x - p.x) * (r.y - q.y); 

        if (val == 0) return 0;  // collinear
        return (val > 0)? 1: 2; // clock or counterclock wise
    } 

    // Prints convex hull of a set of n points.
    public static void convexHull(Point points[], int n)
    {
        // There must be at least 3 points
        if (n < 3) return; 

        // Initialize Result
        Vector<Point> hull = new Vector<Point>(); 

        // Find the leftmost point
        int l = 0;
        for (int i = 1; i < n; i++)
            if (points[i].x < points[l].x)
                l = i; 

        // Start from leftmost point, keep moving
        // counterclockwise until reach the start point
        // again. This loop runs O(h) times where h is
        // number of points in result or output.
        int p = l, q;
        do
        {
            // Add current point to result
            hull.add(points[p]); 

            // Search for a point 'q' such that
            // orientation(p, x, q) is counterclockwise
            // for all points 'x'. The idea is to keep
            // track of last visited most counterclock-
            // wise point in q. If any point 'i' is more
            // counterclock-wise than q, then update q.
            q = (p + 1) % n; 

            for (int i = 0; i < n; i++)
            {
               // If i is more counterclockwise than
               // current q, then update q
               if (orientation(points[p], points[i], points[q])
                                                   == 2)
                   q = i;
            } 

            // Now q is the most counterclockwise with
            // respect to p. Set p as q for next iteration,
            // so that q is added to result 'hull'
            p = q; 

        } while (p != l);  // While we don't come to first
                           // point 

        // Print Result
        for (Point temp : hull)
            System.out.println("(" + temp.x + ", " +
                                temp.y + ")");
    } 

    /* Driver program to test above function */
    public static void main(String[] args)
    { 

        Point points[] = new Point[7];
        points[0]=new Point(0, 3);
        points[1]=new Point(2, 3);
        points[2]=new Point(1, 1);
        points[3]=new Point(2, 1);
        points[4]=new Point(3, 0);
        points[5]=new Point(0, 0);
        points[6]=new Point(3, 3); 

        int n = points.length;
        convexHull(points, n); 

    }
}