旋转矩阵（Rotation Matrix）的推导及其应用

向量的平移，比较简单。

缩放也较为简单

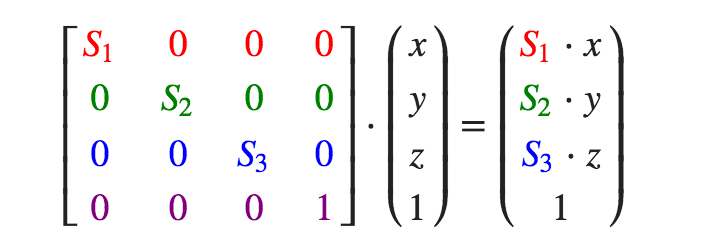
矩阵如何进行计算呢？之前的文章中有简介一种方法，把行旋转一下，然后与右侧对应相乘。在谷歌图片搜索旋转矩阵时，看到这张动图，觉得表述的很清晰了。

稍微复杂一点的是旋转，如果只是二维也很简单（因为很直观），但因为是三维的，有xyz三个轴，先推导二维的再延伸到三维。

YouTube上有很好的推导过程，视频链接地址（需穿.墙） https://www.youtube.com/watch?v=8XRvpDhTJpw

有点P（Xa，Ya），当坐标由 x –> y 旋转 θ 度后，求该点在新坐标轴的坐标是多少

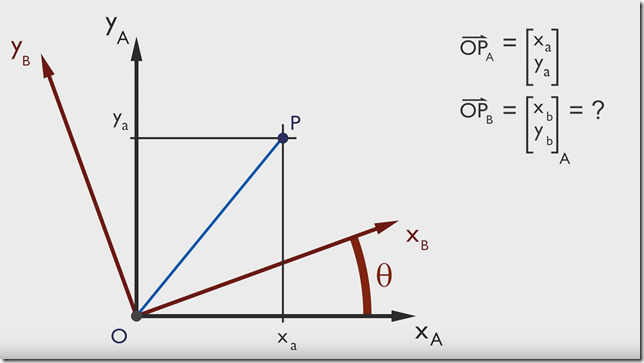
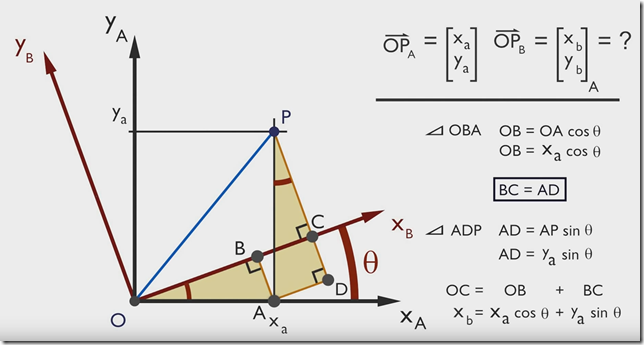
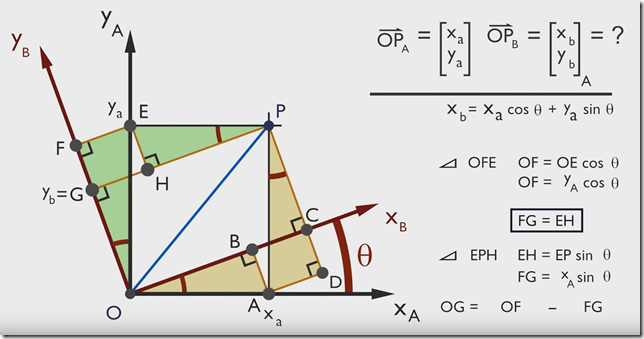
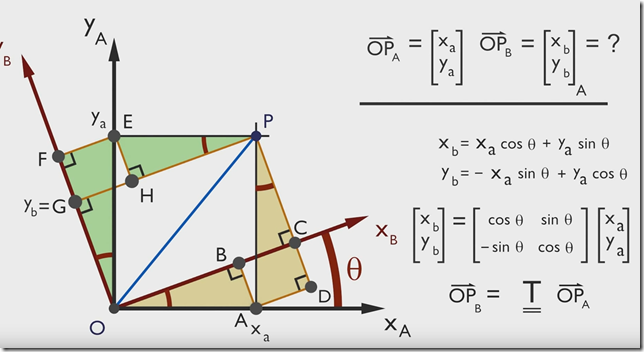
所以对于二维旋转来讲，旋转矩阵就是

三维旋转，需要先搞清楚正、负方向（使用的是右手法则，在二维平面增加一维z，它的正方向朝向屏幕外）。

绕x轴进行旋转（在yz平面顺时针旋转）

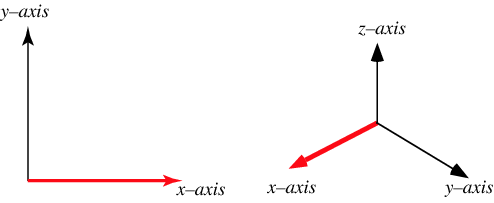
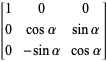
绕y轴进行旋转（在zx平面顺时针旋转）

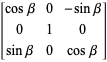
绕z轴进行旋转（在xy平面顺时针旋转）

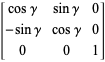
— 图片来源：http://mathworld.wolfram.com/RotationMatrix.html

参考：https://zh.wikipedia.org/wiki/旋转矩阵

了解这些有什么用处呢？之前有讲到渲染被分为三个阶段：应用 –> 几何 –> 栅格化，其中几何阶段做了大量的变换工作。

模型空间 –>( 模型矩阵) –> 世界空间 –> （视图矩阵） –> 观察空间（摄像机，右手坐标系，其余均采用左手） –> （投影矩阵） –> 裁剪空间 –> 屏幕空间，每一次变换都对应着相应的矩阵。

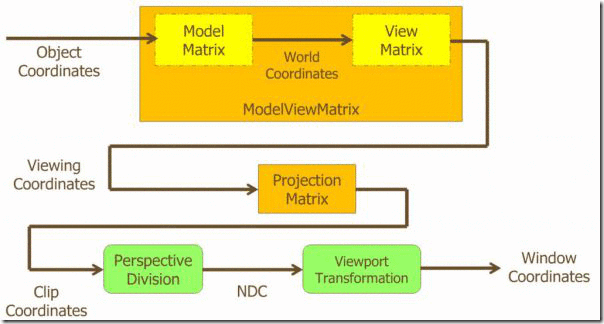
而Unity中的 UNITY_MATRIX_MVP 矩阵表示的是从模型到裁剪坐标的矩阵变换，Model Matrix ● View Matrix ● Projection Matrix。在Unity2017中使用 UnityObjectToClipPos 进行了替换，MVP也即是 模型（M）、视图（V）、透视（P）三个单词的首字母简写。

了解上面这些，才更容易理解Unity内置的变换矩阵

变量名	描述
UNITY_MATRIX_MVP	当前的模型观察投影矩阵，用于将顶点/方向矢量从模型空间变换到裁剪空间
UNITY_MATRIX_MV	当前的模型观察矩阵，用于将顶点/方向矢量从模型空间变换到观察空间
UNITY_MATRIX_V	当前的观察矩阵，用于将顶点/方向矢量从世界空间变换到观察空间
UNITY_MATRIX_P	当前的投影矩阵，用于将顶点/方向矢量从观察空间变换到裁剪空间
UNITY_MATRIX_VP	当前的观察投影矩阵，用于将顶点/方向矢量从世界空间变换到裁剪空间
UNITY_MATRIX_T_MV	UNITY_MATRIX_MV的转置矩阵
UNITY_MATRIX_IT_MV	UNITY_MATRIX_MV人逆转置矩阵，用于将法线从模型空间变换到观察空间，也可以用于得到UNITY_MATRIX_MV的逆矩阵
_Object2World	当前的模型矩阵，用于将顶点/方向矢量从模型空间变换到世界空间（依上面规则，这个其实相当于UNITY_MATRIX_M  即模型空间 –> 世界空间）
_World2Object	_Object2World的逆矩阵，用于将顶点/方向矢量从世界空间变换到模型空间

对照下面这张图，更容易理解一些。

上面这些是基础，只有掌握这些之后，再配置切线、法线、光照模型，在写顶点着色器（Vertex Shader）的时候才不至于懞圈