洛谷 P8742题解

简单版（P2347）传送门

原题传送门

有一道类似的题目（P2347），先扯一扯~

---

1.P2347

题目分析

动态规划入门题（01背包可行性问题）~

我们设 \(dp_j\) 为能否用砝码称出 \(j\) 重量，1 为可以，0 为不可以。

• 为了转移，\(dp_{_{0}} \gets 1\)，什么都不放时，重量为 0，因此可以称出。

那么枚举 \(dp_{_{1}} \sim dp_{sum}(sum\) 为砝码可称出的最大重量\()\)。

• 如果 \(j-w\) 可以称出，且重量为 \(w\) 的砝码存在、未超出个数限制，则 \(j\) 可以称出。即 \(dp_j = dp_{j - w}(j - w \geqslant 0)\)

那么动态转移方程显而易见：

• \(dp_j = dp_{ j - a_i \times k} (j - a_i \times k \geqslant 0 , k \leqslant b_i)\)

PS：\(a_i\)：砝码 \(i\) 的重量，\(b_i\)：砝码 \(i\) 有的个数。

代码

#include<bits/stdc++.h>
using namespace std;
int n = 6, ans = 0, sum = 0;
int dp[1100], a[10] = {0, 1, 2, 3, 5, 10, 20}, b[200];
int main()
{
	fill(dp, dp + 1100, 0);
	for (int i = 1; i <= n; i++) cin >> b[i], sum += a[i] * b[i];
	dp[0] = 1;
	for (int i = 1; i <= n; i++){
		for (int j = sum; j >= 0; j--){ //反着来，不然会重复
			for (int k = 1; k <= b[i]; k++){
				if (dp[j - a[i]*k] == 1 and j - a[i]*k >= 0 and dp[j] == 0)
					dp[j] = 1,ans++;
			}
		}
	}

	cout << "Total=" << ans;
	return 0;
}

2.P8742

题目分析

因为砝码可以放另一边，即减去这个砝码的重量，所以反着还要再来遍历一遍。

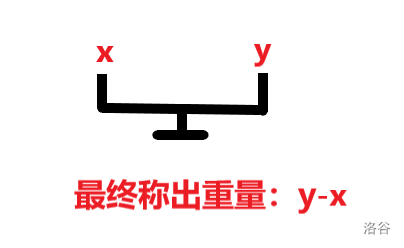
如果 \(dp[j] + a[i] = 1\) 那么 \(dp[j] \gets 1\) 。

转移方程：

• \(dp_j = dp_{ j - a_i } (j - a_i \geqslant 0)\)

• \(dp_j = dp_{ j + a_i } (j + a_i \leqslant sum)\)

代码

#include <bits/stdc++.h>
using namespace std;
int dp[100010], a[110];
long long sum = 0, ans = 0;
int main()
{
	int n;
	cin >> n;
	fill(dp, dp + 100010, 0);
	dp[0] = 1;
	for (int i = 0; i < n; i++)
		cin >> a[i], sum += a[i];
	for (int i = 0; i < n; i++){
		for (int j = sum; j >= a[i]; j--){ //优化，不枚举i<a[j]的情况
			if (dp[j - a[i]] == 1 and dp[j] != 1)
				dp[j] = 1, ans++;
		}
	}
	for (int i = 0; i < n; i++){
		for (int j = 1; j <= sum - a[i]; j++){ //同理
			if (dp[j + a[i]] == 1 and dp[j] == 0)
					dp[j] = 1, ans++;
		}
	}
	cout << ans;
	return 0;
}