AVL树平衡旋转详解

概述

AVL树又叫做平衡二叉树。前言部分我也有说到，AVL树的前提是二叉排序树(BST或叫做二叉查找树)。由于在生成BST树的过程中可能会出现线型树结构，比如插入的顺序是：1, 2, 3, 4, 5, 6, 7..., n。在BST树中，比较理想的状况是每个子树的左子树和右子树的高度相等，此时搜索的时间复杂度是log(N)。可是，一旦这棵树演化成了线型树的时候，这个理想的情况就不存在了，此时搜索的时间复杂度是O(N)，在数据量很大的情况下，我们并不愿意看到这样的结果。

现在我们要做的事就是让BST在创建的过程中不要向线型树发展。方法就是让其在添加新节点的时候，不断调整树的平衡状态。

定义：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

AVL树实现

1.节点失衡

我们对于节点平衡有这样的定义：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。而这里提到的高度差，就是我们下面会引入的平衡因子：BF（balance factor）。

因为AVL树说到底还是一个二叉树，只有两个子节点。而且节点失衡的发生，是因为有一个新节点的插入，这个新插入的节点导致了某些节点左右子节点高度的不一致。所以我们可以枚举出以下4种情况的失衡状态。

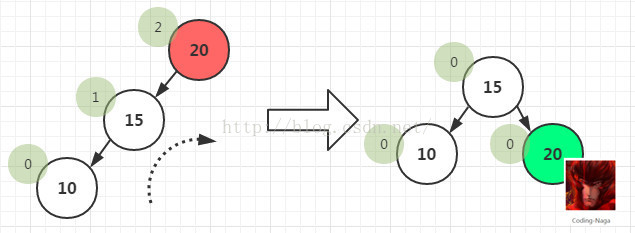
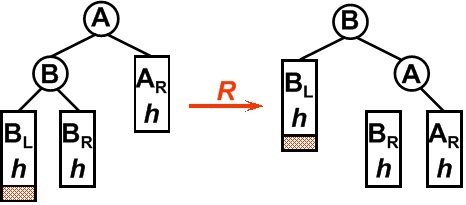
(1)在一个节点的左子树的左子树上插入一个新节点。即LL。在这种情况下，我们可以通过将节点右旋使其平衡。如图-2所示

图-2 LL单右旋操作

原A的左孩子B变为父结点，A变为其右孩子，而原B的右子树变为A的左子树，注意旋转之后Brh是A的左子树。

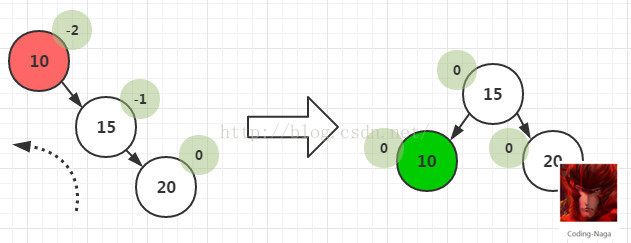
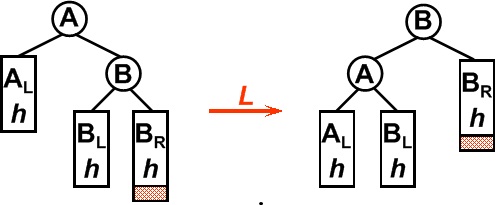
(2)在一个节点的右子树的右子树上插入一个新节点。即RR。在这种情况下，我们可以通过将节点左旋使其平衡。如图-3所示；

图-3 RR单左旋操作

这时只需要把树向左旋转一次即可，如图所示，原A右孩子B变为父结点，A变为其左孩子，而原B的左子树Blh将变为A的右子树。

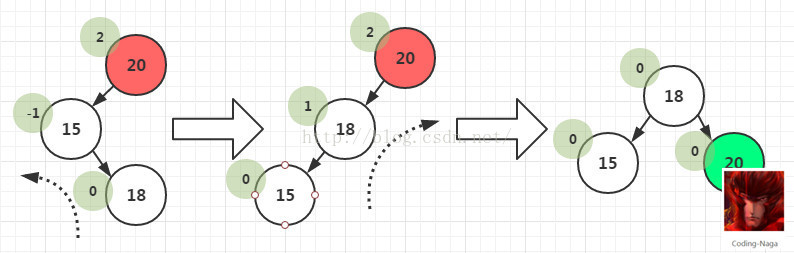
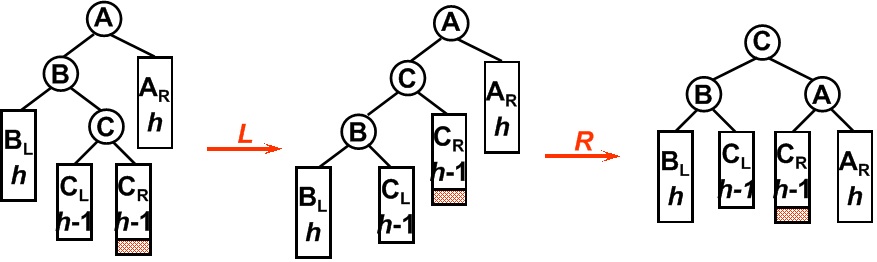
(3)在一个节点的左子树的右子树上插入一个新节点。即LR。在这种情况下，我们不能直接通过将节点左旋或右来使其平衡了。这里需要两步来完成，先让树中高度较低的进行一次左旋（RR型），这个时候就变成了LL了。再进行一次单右旋操作即可。如图-4所示；

图-4 LR先左旋再右旋操作

这时需要旋转两次，仅一次的旋转是不能够使二叉树再次平衡。如图所示，在B节点按照RR型向左旋转一次之后，二叉树在A节点仍然不能保持平衡，这时还需要再向右旋转一次。

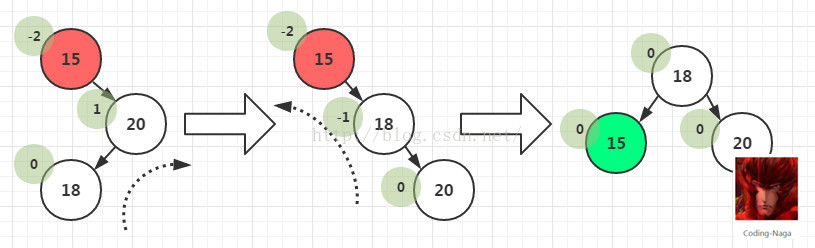
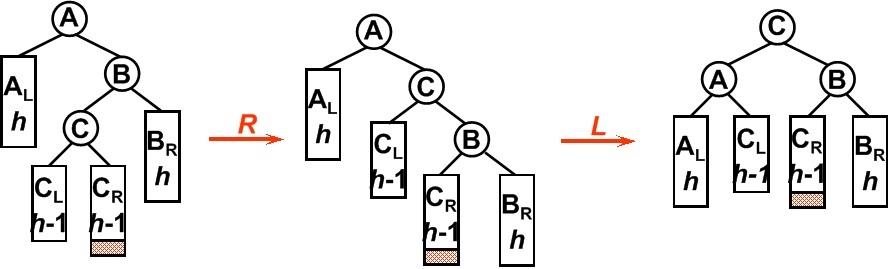
(4)在一个节点的右子树的左子树上插入一个新节点。即RL。在这种情况下，我们不能直接通过将节点左旋或右来使其平衡了。这里需要两步来完成，先让树中高度较低的进行一次右旋，这个时候就变成了RR了。再进行一次单左旋操作即可。如图-5所示；

图-5 RL先右旋再左旋操作

平衡二叉树某一节点的右孩子的左子树上插入一个新的节点，使得该节点不再平衡。同样，这时需要旋转两次，旋转方向刚好同LR型相反。

从上面对节点失衡的说明，以及图解。我想你已经对旋转的操作有了一个大概地认识了吧。从图中我们也可以看出，LL型和RR型、LR型和RL型是两个行为很相似地操作。其实他们互为对称。

代码见这里