【深度学习】L1正则化和L2正则化

在机器学习中，我们非常关心模型的预测能力，即模型在新数据上的表现，而不希望过拟合现象的的发生，我们通常使用正则化（regularization）技术来防止过拟合情况。正则化是机器学习中通过显式的控制模型复杂度来避免模型过拟合、确保泛化能力的一种有效方式。如果将模型原始的假设空间比作“天空”，那么天空飞翔的“鸟”就是模型可能收敛到的一个个最优解。在施加了模型正则化后，就好比将原假设空间（“天空”）缩小到一定的空间范围（“笼子”），这样一来，可能得到的最优解能搜索的假设空间也变得相对有限。有限空间自然对应复杂度不太高的模型，也自然对应了有限的模型表达能力。这就是“正则化有效防止模型过拟合的”一种直观解析。

L2正则化

在深度学习中，用的比较多的正则化技术是L2正则化，其形式是在原先的损失函数后边再加多一项：\(\frac{1}{2}\lambda\theta_{i}^2\)，那加上L2正则项的损失函数就可以表示为：\(L(\theta)=L(\theta)+\lambda\sum_{i}^{n}\theta_{i}^2\)，其中\(\theta\)就是网络层的待学习的参数，\(\lambda\)则控制正则项的大小，较大的取值将较大程度约束模型复杂度，反之亦然。

L2约束通常对稀疏的有尖峰的权重向量施加大的惩罚，而偏好于均匀的参数。这样的效果是鼓励神经单元利用上层的所有输入，而不是部分输入。所以L2正则项加入之后，权重的绝对值大小就会整体倾向于减少，尤其不会出现特别大的值（比如噪声），即网络偏向于学习比较小的权重。所以L2正则化在深度学习中还有个名字叫做“权重衰减”（weight decay），也有一种理解这种衰减是对权值的一种惩罚，所以有些书里把L2正则化的这一项叫做惩罚项（penalty）。

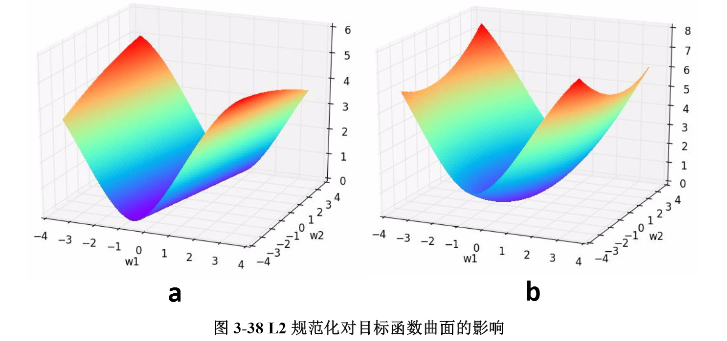
我们通过一个例子形象理解一下L2正则化的作用，考虑一个只有两个参数\(w_{1}\)和\(w_{2}\)的模型，其损失函数曲面如下图所示。从a可以看出，最小值所在是一条线，整个曲面看起来就像是一个山脊。那么这样的山脊曲面就会对应无数个参数组合，单纯使用梯度下降法难以得到确定解。但是这样的目标函数若加上一项\(0.1\times(w_{1}^2+w_{2}^2)\)，则曲面就会变成b图的曲面，最小值所在的位置就会从一条山岭变成一个山谷了,此时我们搜索该目标函数的最小值就比先前容易了，所以L2正则化在机器学习中也叫做“岭回归”（ridge regression）。

L1正则化

L1正则化的形式是：\(\lambda|\theta_{i}|\),与目标函数结合后的形式就是：\(L(\theta)=L(\theta)+\lambda\sum_{i}^{n}|\theta_{i}|\)。需注意，L1 正则化除了和L2正则化一样可以约束数量级外，L1正则化还能起到使参数更加稀疏的作用，稀疏化的结果使优化后的参数一部分为0，另一部分为非零实值。非零实值的那部分参数可起到选择重要参数或特征维度的作用，同时可起到去除噪声的效果。此外，L1正则化和L2正则化可以联合使用：\(\lambda_{1}|\theta_{i}|+\frac{1}{2}\lambda_{2}\theta_{i}^2\)。这种形式也被称为“Elastic网络正则化”。

正则化对偏导的影响

对于L2正则化：\(C=C_{0}+\frac{\lambda}{2n}\sum_{i}\omega_{i}^2\)，相比于未加正则化之前,权重的偏导多了一项\(\frac{\lambda}{n}\omega\)，偏置的偏导没变化，那么在梯度下降时\(\omega\)的更新变为：

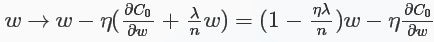
可以看出\(\omega\)的系数使得权重下降加速，因此L2正则也称weight decay(caffe中损失层的weight_decay参数与此有关)。对于随机梯度下降(对一个mini-batch中的所有x的偏导求平均)：

对于L1正则化：\(C=C_{0}+\frac{\lambda}{n}\sum_{i}|\omega_{i}|\)，梯度下降的更新为：

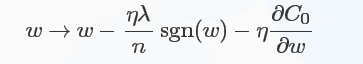
符号函数在\(\omega\)大于0时为1，小于0时为-1，在\(\omega=0\)时\(|\omega|\)没有导数，因此可令sgn(0)=0，在0处不使用L1正则化。

相比于L2，有所不同：

• L1减少的是一个常量，L2减少的是权重的固定比例
• 孰快孰慢取决于权重本身的大小，权重刚大时可能L2快，较小时L1快

实践中L2正则化通常优于L1正则化。