2016年中国大学生程序设计竞赛（合肥）-重现赛1001 HDU 5961

传递

Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 42    Accepted Submission(s): 16

Problem Description

我们称一个有向图G是传递的，当且仅当对任意三个不同的顶点a,,若G中有 一条边从a到b且有一条边从b到c ,则G中同样有一条边从a到c。
我们称图G是一个竞赛图，当且仅当它是一个有向图且它的基图是完全图。换句 话说，将完全图每条边定向将得到一个竞赛图。
下图展示的是一个有4个顶点的竞赛图。

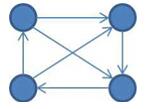
现在，给你两个有向图P = (V,Ep

)和Q = (V,Ee

)，满足:
1.   EP

与Ee

没有公共边；
2.  (V,Ep⋃Ee

)是一个竞赛图。
你的任务是：判定是否P，Q同时为传递的。

 

Input

包含至多20组测试数据。
第一行有一个正整数，表示数据的组数。
对于每组数据，第一行有一个正整数n。接下来n行，每行为连续的n个字符，每 个字符只可能是’-’,’P’,’Q’中的一种。
∙

如果第i行的第j个字符为’P’，表示有向图P中有一条边从i到j;
∙

如果第i行的第j个字符为’Q’，表示有向图Q中有一条边从i到j;
∙

否则表示两个图中均没有边从i到j。
保证1 <= n <= 2016，一个测试点中的多组数据中的n的和不超过16000。保证输入的图一定满足给出的限制条件。

 

Output

对每个数据，你需要输出一行。如果P! Q都是传递的，那么请输出’T’。否则， 请输出’N’ (均不包括引号)。

 

Sample Input

4
4
-PPP
--PQ
---Q
----
4
-P-P
--PQ
P--Q
----
4
-PPP
--QQ
----
--Q-
4
-PPP
--PQ
----
--Q-

 

Sample Output

T
N
T
N

Hint

在下面的示意图中，左图为图为Q。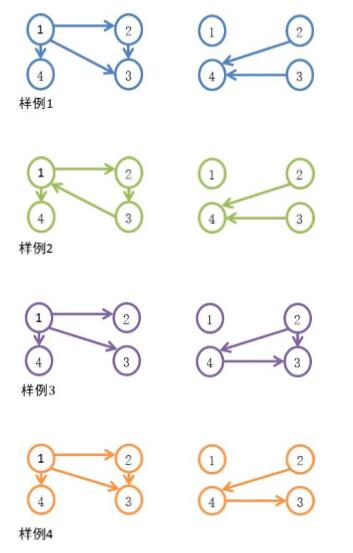
注：在样例2中，P不是传递的。在样例4中，Q不是传递的。

 

Source

2016年中国大学生程序设计竞赛（合肥）-重现赛（感谢安徽大学）

 

题意：中文题面

题解：a->b->c 枚举中间点b 判断中间点的先驱点集a 的后继点集合是否含于c

  bitset 处理；

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<vector>
 #include<bitset>
 #define ll __int64
 using namespace std;
 int t;
 char mp[][];
 vector<int> p[];
 vector<int> q[];
 struct  node
 {
      bitset<> from;
     bitset<> to;
 } pp[],qq[];
 int n;
 void init()
 {
     for(int i=; i<n; i++)
     {
         p[i].clear();
         q[i].clear();
         pp[i].from.reset();
         pp[i].to.reset();
         qq[i].from.reset();
         qq[i].to.reset();
     }
 }
 int main()
 {
     scanf("%d",&t);
     for(int i=; i<=t; i++)
     {
         scanf("%d",&n);
         init();
         for(int j=; j<n; j++)
             scanf("%s",mp[j]);
         for(int j=; j<n; j++)
         {
             for(int k=; k<n; k++)
             {
                 if(mp[j][k]=='P')
                     p[j].push_back(k);
                 if(mp[j][k]=='Q')
                     q[j].push_back(k);
             }
         }
         int flag1=,flag2=;
         for(int k=; k<n; k++)
         {
             for(int j=;j<p[k].size();j++)
             {
                 pp[k].to[p[k][j]]=;
                 pp[p[k][j]].from[k]=;
             }
             for(int j=;j<q[k].size();j++)
             {
                 qq[k].to[q[k][j]]=;
                 qq[q[k][j]].from[k]=;
             }
         }
         for(int k=; k<n; k++)
         {
             for(int l=; l<n; l++)
             {
                  if(pp[k].from[l]==)
                 {
                     bitset<> exm;
                     exm=pp[l].to&pp[k].to;
                     if(exm!=pp[k].to)
                     {
                         flag1=;
                         break;
                     }
                 }
             }
             for(int l=; l<n; l++)
             {
                 if(qq[k].from[l]==)
                 {
                     bitset<> exm;
                     exm=qq[l].to&qq[k].to;
                     if(exm!=qq[k].to)
                     {
                         flag2=;
                         break;
                     }
                 }
             }
         }
         if(flag1&&flag2)
             cout<<"T"<<endl;
         else
             cout<<"N"<<endl;
     }
     return ;
 }