HDU 1890 Robotic Sort （splay tree）

Robotic Sort

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1640    Accepted Submission(s): 711

Problem Description

Somewhere deep in the Czech Technical University buildings, there are laboratories for examining mechanical and electrical properties of various materials. In one of yesterday’s presentations, you have seen how was one of the laboratories changed into a new multimedia lab. But there are still others, serving to their original purposes.

In this task, you are to write software for a robot that handles samples in such a laboratory. Imagine there are material samples lined up on a running belt. The samples have different heights, which may cause troubles to the next processing unit. To eliminate such troubles, we need to sort the samples by their height into the ascending order.

Reordering is done by a mechanical robot arm, which is able to pick up any number of consecutive samples and turn them round, such that their mutual order is reversed. In other words, one robot operation can reverse the order of samples on positions between A and B.

A possible way to sort the samples is to find the position of the smallest one (P1) and reverse the order between positions 1 and P1, which causes the smallest sample to become first. Then we find the second one on position P and reverse the order between 2 and P2. Then the third sample is located etc.

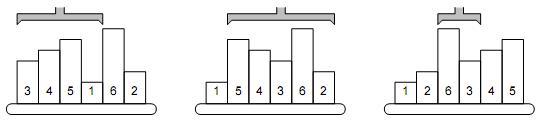
The picture shows a simple example of 6 samples. The smallest one is on the 4th position, therefore, the robot arm reverses the first 4 samples. The second smallest sample is the last one, so the next robot operation will reverse the order of five samples on positions 2–6. The third step will be to reverse the samples 3–4, etc.

Your task is to find the correct sequence of reversal operations that will sort the samples using the above algorithm. If there are more samples with the same height, their mutual order must be preserved: the one that was given first in the initial order must be placed before the others in the final order too.

 

Input

The input consists of several scenarios. Each scenario is described by two lines. The first line contains one integer number N , the number of samples, 1 ≤ N ≤ 100 000. The second line lists exactly N space-separated positive integers, they specify the heights of individual samples and their initial order.

The last scenario is followed by a line containing zero.

 

Output

For each scenario, output one line with exactly N integers P1 , P1 , . . . PN ,separated by a space.
Each Pi must be an integer (1 ≤ Pi ≤ N ) giving the position of the i-th sample just before the i-th reversal operation.

Note that if a sample is already on its correct position Pi , you should output the number Pi anyway, indicating that the “interval between Pi and Pi ” (a single sample) should be reversed.

 

Sample Input

6
3 4 5 1 6 2
4
3 3 2 1
0

 

Sample Output

4 6 4 5 6 6
4 2 4 4

 

Source

2008 “Shun Yu Cup” Zhejiang Collegiate Programming Contest - Warm Up（2）

 

Recommend

linle

 

splay tree

旋转操作

 /* ***********************************************
 Author        :kuangbin
 Created Time  :2013/8/24 23:28:43
 File Name     :F:\2013ACM练习\专题学习\splay_tree_2\HDU1890.cpp
 ************************************************ */

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <string>
 #include <math.h>
 #include <stdlib.h>
 #include <time.h>
 using namespace std;

 #define Key_value ch[ch[root][1]][0]
 const int MAXN = ;
 int pre[MAXN],ch[MAXN][],root,tot1;
 int size[MAXN];//子树规模
 int rev[MAXN];//反转标记
 int s[MAXN],tot2;//内存池和容量

 //debug部分**********************************
 void Treavel(int x)
 {
     if(x)
     {
         Treavel(ch[x][]);
         printf("结点：%2d: 左儿子 %2d 右儿子 %2d 父结点 %2d size = %2d rev = %2d\n",x,ch[x][],ch[x][],pre[x],size[x],rev[x]);
         Treavel(ch[x][]);
     }
 }
 void debug()
 {
     printf("root:%d\n",root);
     Treavel(root);
 }
 //以上是debug部分**************************************

 void NewNode(int &r,int father,int k)
 {
     r = k;
     pre[r] = father;
     ch[r][] = ch[r][] = ;
     size[r] = ;
     rev[r] = ;
 }
 //反转的更新
 void Update_Rev(int r)
 {
     if(!r)return;
     swap(ch[r][],ch[r][]);
     rev[r] ^= ;
 }
 inline void push_up(int r)
 {
     size[r] = size[ch[r][]] + size[ch[r][]] + ;
 }
 inline void push_down(int r)
 {
     if(rev[r])
     {
         Update_Rev(ch[r][]);
         Update_Rev(ch[r][]);
         rev[r] = ;
     }
 }
 void Build(int &x,int l,int r,int father)
 {
     if(l > r)return;
     int mid = (l+r)/;
     NewNode(x,father,mid);
     Build(ch[x][],l,mid-,x);
     Build(ch[x][],mid+,r,x);
     push_up(x);
 }
 int n;
 void Init()
 {
     root = tot1 = tot2 = ;
     ch[root][] = ch[root][] = pre[root] = size[root] = rev[root] = ;
     NewNode(root,,n+);
     NewNode(ch[root][],root,n+);
     Build(Key_value,,n,ch[root][]);
     push_up(ch[root][]);
     push_up(root);
 }
 //旋转，0为左旋，1为右旋
 inline void Rotate(int x,int kind)
 {
     int y = pre[x];
     push_down(y);
     push_down(x);//先把y的标记下传，在把x的标记下传
     ch[y][!kind] = ch[x][kind];
     pre[ch[x][kind]] = y;
     if(pre[y])
         ch[pre[y]][ch[pre[y]][]==y] = x;
     pre[x] = pre[y];
     ch[x][kind] = y;
     pre[y] = x;
     push_up(y);
 }
 //Splay调整，将r结点调整到goal下面
 inline void Splay(int r,int goal)
 {
     push_down(r);
     while(pre[r] != goal)
     {
         if(pre[pre[r]] == goal)
         {
             //有反转操作，需要先push_down,再判断左右孩子
             push_down(pre[r]);
             push_down(r);
             Rotate(r,ch[pre[r]][]==r);
         }
         else
         {
             //有反转操作，需要先push_down
             push_down(pre[pre[r]]);
             push_down(pre[r]);
             push_down(r);
             int y = pre[r];
             int kind = ch[pre[y]][]==y;
             if(ch[y][kind] == r)
             {
                 Rotate(r,!kind);
                 Rotate(r,kind);
             }
             else
             {
                 Rotate(y,kind);
                 Rotate(r,kind);
             }
         }
     }
     push_up(r);
     if(goal == ) root = r;
 }
 //得到第k个结点(需要push_down)
 inline int Get_kth(int r,int k)
 {
     push_down(r);
     int t = size[ch[r][]] + ;
     if(t == k)return r;
     if(t > k)return Get_kth(ch[r][],k);
     else return Get_kth(ch[r][],k-t);
 }
 //找前驱(需要push_down)
 inline int Get_pre(int r)
 {
     push_down(r);
     if(ch[r][] == )return -;//不存在
     r = ch[r][];
     while(ch[r][])
     {
         r = ch[r][];
         push_down(r);
     }
     return r;
 }
 //找后继(需要push_down)
 inline int Get_next(int r)
 {
     push_down(r);
     if(ch[r][] == )return -;
     r = ch[r][];
     while(ch[r][])
     {
         r = ch[r][];
         push_down(r);
     }
     return r;
 }

 struct Node
 {
     int id,val;
 }node[MAXN];
 bool cmp(Node a,Node b)
 {
     if(a.val != b.val)return a.val < b.val;
     else return a.id < b.id;
 }
 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
      while(scanf("%d",&n) ==  && n)
     {
         for(int i = ;i <= n;i++)
         {
             scanf("%d",&node[i].val);
             node[i].id = i;
         }
         sort(node+,node+n+,cmp);
         Init();
         for(int i = ; i <= n;i++)
         {
             Splay(node[i].id,);
             printf("%d",size[ch[root][]]);
             if(i < n)printf(" ");
             else printf("\n");
             Splay(Get_kth(root,i),);
             Splay(Get_next(node[i].id),root);
             Update_Rev(Key_value);
         }
     }
     return ;
 }