7-n!的位数（斯特灵公式）

http://acm.hdu.edu.cn/showproblem.php?pid=1018　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　Big Number
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 40483 Accepted Submission(s): 19774

Problem Description
In many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number.

Input
Input consists of several lines of integer numbers. The first line contains an integer n, which is the number of cases to be tested, followed by n lines, one integer 1 ≤ n ≤ 107 on each line.

Output
The output contains the number of digits in the factorial of the integers appearing in the input.

Sample Input
2
10
20

Sample Output
7
19

Source
Asia 2002, Dhaka (Bengal)

分析：

斯特灵公式是一条用来取n阶乘近似值的数学公式。

公式为：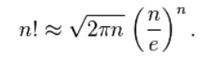

斯特林公式可以用来估算某数的大小，结合lg可以估算某数的位数，或者可以估算某数的阶乘是另一个数的倍数。

题意：
给你一个整数n，求n！的位数。
利用 求解n!的位数：

易知整数n的位数为[lgn]+1。.利用Stirling公式计算n!结果的位数时，可以两边取对数，得:
log10(n!) = log10(2*n*Pi)/2+n*log10(n/e)
则答案为：
ans = log10(2*n*Pi)/2+n*log10(n/e) + 1
其他类型题：hdu4045 hdu2521

如果是求八进制的位数呢：http://www.cnblogs.com/zhumengdexiaobai/p/8415053.html

#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
double e = 2.718281828459045;
double pi = 3.141592653589793;

int main(){
	int t, n;
	cin >> t;

	while(t--){
		cin >> n;
		double k = log10(2 * pi * n) / 2 + n * log10(n / e);
//		cout << ceil(k) << endl;   //不能直接向上取整，因为若是刚好是整数，则会小1： 1.1e4,应该是4+1
		cout << (int)k + 1 << endl;
	}

	return 0;
}