线性回归和批量梯度下降法python

通过学习斯坦福公开课的线性规划和梯度下降，参考他人代码自己做了测试，写了个类以后有时间再去扩展，代码注释以后再加，作业好多：

import numpy as np
import matplotlib.pyplot as plt
import random

class dataMinning:
    datasets = []
    labelsets = []

    addressD = ''  #Data folder
    addressL = ''  #Label folder

    npDatasets = np.zeros(1)
    npLabelsets = np.zeros(1)

    cost = []
    numIterations = 0
    alpha = 0
    theta = np.ones(2)
    #pCols = 0
    #dRows = 0
    def __init__(self,addressD,addressL,theta,numIterations,alpha,datasets=None):
        if datasets is None:
            self.datasets = []
        else:
            self.datasets = datasets
        self.addressD = addressD
        self.addressL = addressL
        self.theta = theta
        self.numIterations = numIterations
        self.alpha = alpha

    def readFrom(self):
        fd = open(self.addressD,'r')
        for line in fd:
            tmp = line[:-1].split()
            self.datasets.append([int(i) for i in tmp])
        fd.close()
        self.npDatasets = np.array(self.datasets)

        fl = open(self.addressL,'r')
        for line in fl:
            tmp = line[:-1].split()
            self.labelsets.append([int(i) for i in tmp])
        fl.close()

        tm = []
        for item in self.labelsets:
            tm = tm + item
        self.npLabelsets = np.array(tm)

    def genData(self,numPoints,bias,variance):
        self.genx = np.zeros(shape = (numPoints,2))
        self.geny = np.zeros(shape = numPoints)

        for i in range(0,numPoints):
            self.genx[i][0] = 1
            self.genx[i][1] = i
            self.geny[i] = (i + bias) + random.uniform(0,1) * variance

    def gradientDescent(self):
        xTrans = self.genx.transpose() #
        i = 0
        while i < self.numIterations:
            hypothesis = np.dot(self.genx,self.theta)
            loss = hypothesis - self.geny
            #record the cost
            self.cost.append(np.sum(loss ** 2))
            #calculate the gradient
            gradient = np.dot(xTrans,loss)
            #updata, gradientDescent
            self.theta = self.theta - self.alpha * gradient
            i = i + 1

    def show(self):
        print 'yes'

if __name__ == "__main__":
    c = dataMinning('c:\\city.txt','c:\\st.txt',np.ones(2),100000,0.000005)
    c.genData(100,25,10)
    c.gradientDescent()
    cx = range(len(c.cost))
    plt.figure(1)
    plt.plot(cx,c.cost)
    plt.ylim(0,25000)
    plt.figure(2)
    plt.plot(c.genx[:,1],c.geny,'b.')
    x = np.arange(0,100,0.1)
    y = x * c.theta[1] + c.theta[0]
    plt.plot(x,y)
    plt.margins(0.2)
    plt.show()

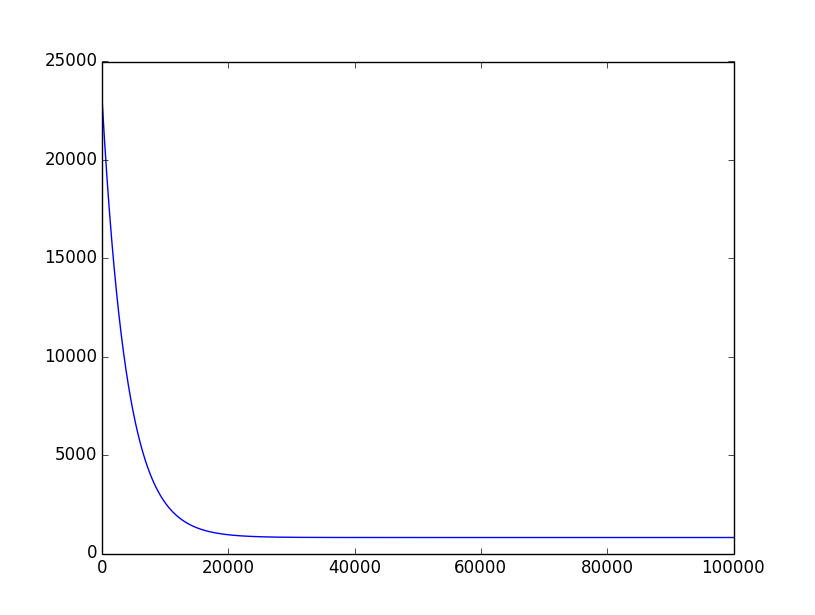
　　　　　　　　　　图1. 迭代过程中的误差cost

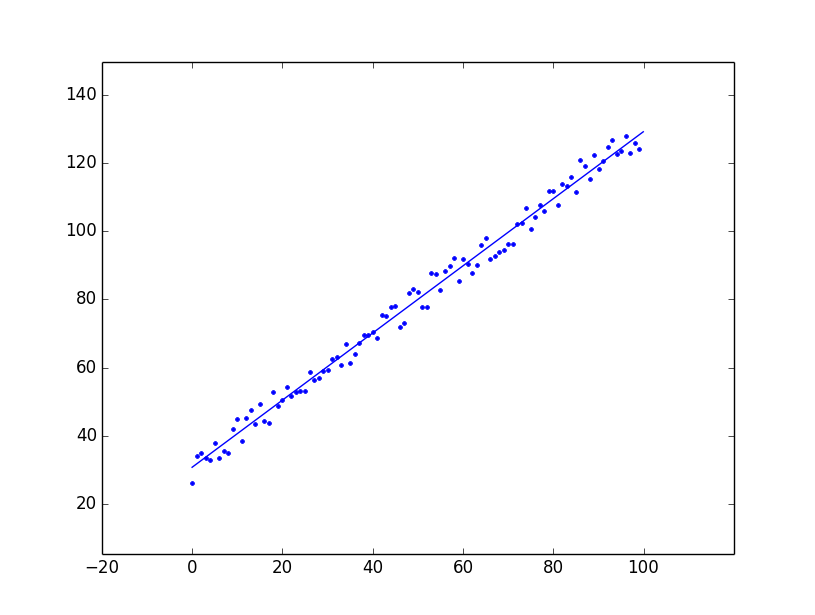
　　　　　　　　　　图2. 数据散点图和解直线

参考资料：

1.python编写类：http://blog.csdn.net/wklken/article/details/6313265

2.python中if __name__ == __main__的用法：http://www.cnblogs.com/herbert/archive/2011/09/27/2193482.html

3.matplotlab gallery:http://matplotlib.org/gallery.html

4.python批量梯度下降参考代码：http://www.91r.net/ask/17784587.html