P1140 相似基因 这个和之前有一个题目特别像 dp

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了444种核苷酸，简记作A,C,G,TA,C,G,TA,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATGAGTGATGAGTGATG和GTTAGGTTAGGTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

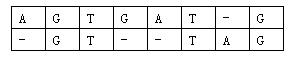
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

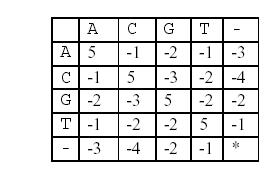
那么相似度就是：(−3)+5+5+(−2)+(−3)+5+(−3)+5=9(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因为两个基因的对应方法不唯一，例如又有：

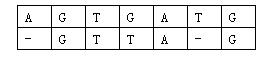
相似度为：(−3)+5+5+(−2)+5+(−1)+5=14(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,TA,C,G,TA,C,G,T四个字母。1≤1 \le 1≤序列的长度≤100 \le 100≤100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1： 复制

7 AGTGATG
5 GTTAG

输出样例#1： 复制

14

这个题目和之前写的比较像，不过预处理有点不一样，就是把ATGC-换成了1 2 3 4 0，我觉得这样子比较好，我不是很会举一反三，做完这个题目之后，对这种类型的题目有了一定的思考。

#include <stdio.h>
#include <string.h>
#include <algorithm>
#include <iostream>
#define inf 0x3f3f3f3f
using namespace std;
typedef long long ll;
int sum[5][5]={{5,-1,-2,-1,-3},
			   {-1,5,-3,-2,-4},
			   {-2,-3,5,-2,-2},
			   {-1,-2,-2,5,-1},
			   {-3,-4,-2,-1,0}
			  };
int dp[110][110];
int tras(char s)
{
	if (s == 'A') return 0;
	if (s == 'C') return 1;
	if (s == 'G') return 2;
	if (s == 'T') return 3;
	if (s == '-') return 4;
}
int min_(int x, int y, int z)
{
	int exa = max(x, y);
	int ans = max(exa, z);
	return ans;
}

int main()
{
	int lena, lenb;
	char a[110], b[110];
	cin >> lena >>(a+1) >> lenb >> (b+1);
	for (int i = 1; i <= lena; i++)
	{
		int x = tras(a[i]);
		dp[i][0] = sum[x][4] + dp[i - 1][0];
	}
	for (int i = 1; i <= lenb; i++)
	{
		int x = tras(b[i]);
		dp[0][i] = sum[4][x] + dp[0][i - 1];
	}
	for (int i = 1; i <= lena; i++)
	{
		for (int j = 1; j <= lenb; j++)
		{
			int p = tras(a[i]);
			int q = tras(b[j]);
			dp[i][j] = min_(dp[i-1][j]+sum[4][p],dp[i][j-1]+sum[4][q],dp[i-1][j-1]+sum[p][q]);//这里要注意是加sum[4][i]这个i要注意是什么
		}
	}
	printf("%d\n", dp[lena][lenb]);
	return 0;
}