Sparse Principal Component Analysis

目录

• 背景:
• 部分符号
• 创新点
• 文章梗概
  • The LASSO AND THE ELASTIC NET
  • 将PCA改造为回归问题
  • 定理二 单个向量（无需进行SVD版本）
  • 定理三 多个向量（无需进行SVD， 非LASSO，非elastic net）
  • 目标函数（最终版）
  • 算法一
  • 方差计算
  • 复杂度
  • \(p \gg n\) 算法改进
• 数值实验（pitprops）

背景:

sparse PCA 较 PCA来说更具可解释性，泛化性。

部分符号

\(\mathrm{X} \in \mathbb{R}^{n \times p}\)
假设样本已经中心化（每一个行为一个样本）
\(\mathrm{X}=[X_1,X_2,\ldots, X_p]\)
\(X_j = (x_{1j}, x_{2j},\ldots, x_{nj})\)
\(\mathrm{X = UDV^{T}}\)
\(\mathrm{Z=UD}\)为主成分（PCs）

创新点

1.将PCA问题转化为一个回归问题，利用最小角回归，可以高效求解Lasso问题。
2.二重迭代求解，sparse PCA问题。

文章梗概

The LASSO AND THE ELASTIC NET

普通的Lasso

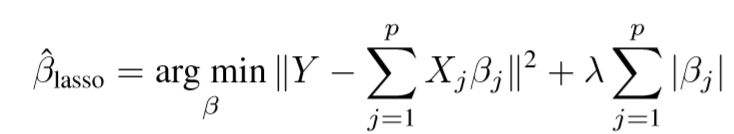
\(Y=(y_1,y_2,\ldots,y_n)^{\mathrm{T}}\)
这个方法的问题在于，当\(p \gg n\)的时候，\(\hat{\beta}\)最多有n个非零项（这是为什么呢？）

The elastic net

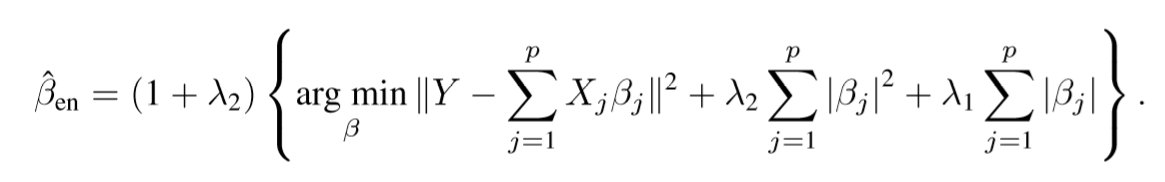
将PCA改造为回归问题

定理一 考虑单个向量（需要先进行SVD）

定理二 单个向量（无需进行SVD版本）

定理三 多个向量（无需进行SVD， 非LASSO，非elastic net）

目标函数（最终版）

俩步求解

定理四 A given B的理论支撑（存疑）

算法一

方差计算

因为稀疏化后的向量，既不具有空间上（往往）的正交性，也不具有概率上（\(\mathrm{x^{T}Cy}=0\)）的正交性。这里，Zou 考虑的是概率上的正交性，将得到的向量正交化，把余量相加得最后的方差。

复杂度

\(n > p\) ： \(np^2+mO(p^3)\) #m是迭代次数

\(p \gg n\) 算法改进

简单来说，就是把step2改进下，原来需要求解一个elastic net问题，现在直接进行截断，自然会减轻不少负担。

数值实验（pitprops）