Splay讲解
Splay讲解
Splay是平衡树的一种,是一种二叉搜索树,我们先讲解一下它的核心部分。
Splay的核心部分就是splay,可能有些人会说什么鬼?这样讲解是不是太不认真了?两个字回答:不是。第一个Splay是算法名称,而第二个splay是一个函数,如果说是一个函数,还不如说是两个函数,splay和rotate。下面开始讲解:
rotate
Splay最重要的部分就是两种基本旋转:zig,zag。本人在此理解的zig是左旋而zag是右旋。学过Treap的人可能会想到Treap的左右两旋,那两个旋转和这两个旋转是不一样的,Treap的旋转是讲自己的儿子旋上来,而Splay的旋转是将自己旋到父亲上去,两者的本质是不同的。
首先先讲解zag:我们要旋转的时候,一定会用到当前节点的父亲,所以我们需要存一个父亲数组,来记录当前节点的父亲是谁。当然我们还需要记录儿子是谁——左右两个儿子。现在就可以开始旋转了,如图(将B号节点旋到他的父亲A号节点的上方),是不是和treap的右旋十分相像?就是treap的右旋是在A号节点完成的,而zag是在B号节点完成的。
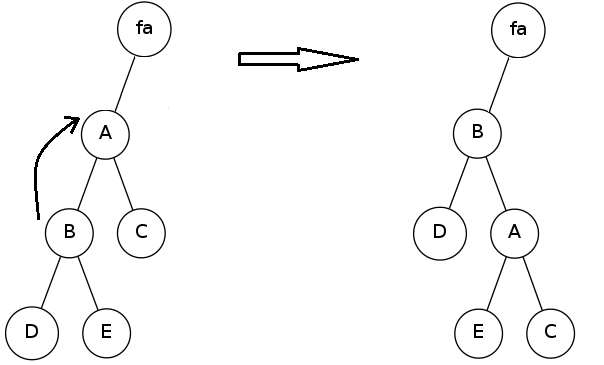
void zag(int p)
{
int tmp=fa[p],tmp2=fa[tmp];
lson[tmp]=rson[p],fa[rson[p]]=tmp;
rson[p]=tmp,fa[tmp]=p,fa[p]=tmp2;
if(lson[tmp2]==tmp) lson[tmp2]=p;
else rson[tmp2]=p;
update(tmp),update(p);
}
同理,zig就十分简单了,如图(将A号节点旋到他的父亲B号节点的上方)。
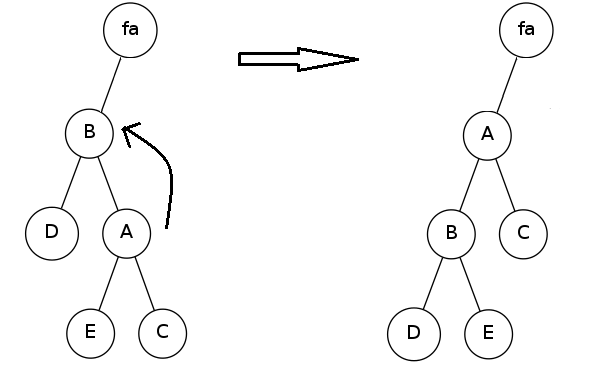
void zig(int p)
{
int tmp=fa[p],tmp2=fa[tmp];
rson[tmp]=lson[p],fa[lson[p]]=tmp;
lson[p]=tmp,fa[tmp]=p,fa[p]=tmp2;
if(lson[tmp2]==tmp) lson[tmp2]=p;
else rson[tmp2]=p;
update(tmp),update(p);
}
这就是zig和zag两种旋转,但我们大家仔细思考一下,这两个旋转的代码基本一致,是不是可以合成一个函数?答案是可以。我们开一个数组,为son[p][2],这个数组的含义就是p号节点的左右两个儿子,son[p][0]表示p号节点的左儿子,而son[p][1]表示p号节点的右儿子。这样我们进行旋转就十分方便了,我们进行一次check看我要左旋还是右旋就可以了,我们可以写一个chek函数返回值就是0和1,这样的话直接把返回值放在第二维就好了。
bool check(int p)
{
return p==son[fp][1];
}
void rotate(int p)
{
int tmp=fp;
int tmp2=ftp;
int tmp3;
check(p)?tmp3=1:tmp3=0;
fa[son[tmp][tmp3]=son[p][tmp3^1]]=tmp;
fa[p]=tmp2;
if(tmp2) son[tmp2][check(tmp)]=p;
fa[son[p][tmp3^1]=tmp]=p;
update(tmp),update(p);
}
旋转rotate讲解完毕,有问题可以发评论,我会解答。下面讲解splay,splay的功能就是将当前节点旋转到顶点,实际上就是一个循环。旋转一共有六种组合,下面我会逐个解释。
splay
第一种:当前节点直接就是根节点左儿子,直接zag就好啦。同理第二种:当前节点是根节点的右儿子,直接zig。
第三种(如左一图):我们需要先将当前节点的父亲旋转上去,再将自己旋转上去,就是先zag(父亲),再zag(自己)。同理第四种(如左二图):先zig(父亲),再zig(自己)。
第五种(入右二图):我们需要先将当前节点旋转上去,再讲他的父亲旋转上去,就是先zig(自己),再zag(父亲)。同理第六种(如右一图):先zag(自己),再zig(父亲)。
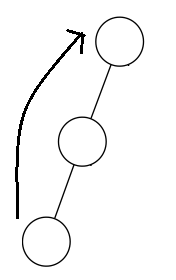
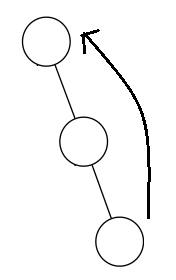
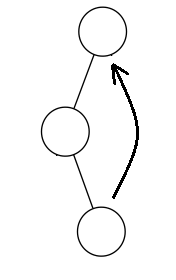
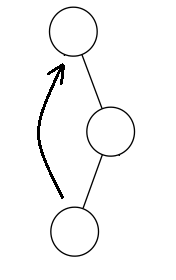
每次旋转的时候我们需要check一下具体实现比较简单。下面的代码是写的将当前节点旋转到指定的节点也就是所写(order),这样写的原因下面会说。
void splay(int p,int &order)
{
int tmp2=fa[order];
for(int tmp;(tmp=fp)!=tmp2;rotate(p))
if(ftp!=tmp2)
rotate(check(p)==check(tmp)?tmp:p);
order=p;
}
splay也讲解完毕,不会的也可以发评论问我。
区间操作
最后讲解一下splay比treap多出的操作,就是区间操作。这也就是为什么像上面那样书写代码,我们如果要对权值为[x,y]的这个区间进行操作,我们可以查找到x-1这个值的节点,将其旋转到root,再找到y+1这个值的节点,将其旋转到root的右儿子上。旋转之后,根据BST的性质,我们可以知道root的右儿子的左子树就是我们要的区间,直接进行操作就好啦,是不是很简单?
问题依旧可以发到评论之中。
Splay讲解的更多相关文章
- 【转】 史上最详尽的平衡树(splay)讲解与模板(非指针版spaly)
ORZ原创Clove学姐: 变量声明:f[i]表示i的父结点,ch[i][0]表示i的左儿子,ch[i][1]表示i的右儿子,key[i]表示i的关键字(即结点i代表的那个数字),cnt[i]表示i结 ...
- 平衡树之splay讲解
首先来说是splay是二叉搜索树,它可以说是线段树和SBT的综合,更可以解决一些二者解决不了的问题,splay几乎所有的操作都是由splay这一操作完成的,在介绍这一操作前我们先介绍几个概念和定义 二 ...
- [bzoj] 1588 营业额统计 || Splay板子题
原题 给出一个n个数的数列ai ,对于第i个元素ai定义\(fi=min(|ai-aj|) (1<=j<i)\),f1=a1,求\(/sumfi\) Splay板子题. Splay讲解:h ...
- 【模板】普通平衡树(权值splay)
安利splay讲解: [洛谷日报第62期]Splay简易教程 [模板]普通平衡树(luogu) Description 题目描述 您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下 ...
- Splay代码简化版
皆さん.こんにちは.上一篇文章,我们讲了Splay如何实现.这一篇我们来让我们的伸展树短一点. 上一篇Splay讲解的链接:リンク. 首先还是变量的定义,在这里呢,我把一些小函数也用Define来实现 ...
- Algorithm lecture
当前标签: lecture 组合数求法讲解 BLADEVIL 2014-01-08 18:59 阅读:3 评论:0 mobius反演讲解 BLADEVIL 2014-01-08 18:13 ...
- 【专题】平衡树(Treap,fhq-treap)
[旋转] 平衡树中的旋转是指在不改变中序遍历的前提下改变树的形态的方式.(中序遍历=排名顺序) 右旋将当前点的左节点旋上来,左旋反之.(图侵删) void rturn(int &k){ int ...
- 平衡树及笛卡尔树讲解(旋转treap,非旋转treap,splay,替罪羊树及可持久化)
在刷了许多道平衡树的题之后,对平衡树有了较为深入的理解,在这里和大家分享一下,希望对大家学习平衡树能有帮助. 平衡树有好多种,比如treap,splay,红黑树,STL中的set.在这里只介绍几种常用 ...
- Play with Chain 【HDU - 3487】【Splay+TLE讲解】
题目链接 很好的一道题,用了三天多的时间,终于知道了我为什么T的原因,也知道了在Splay的同时该怎样子的节约时间,因为Splay本身就是大常数的O(N*logN),我们如果不在各种细节上节约时间,很 ...
随机推荐
- node框架koa
node的两大常见web服务器框架有express和koa,之前已经介绍过express了现在来介绍下koa吧~ koa也是express团队的出品,意在利用es7新出的async来告别"回 ...
- mysql数据库基本操作
下载地址 http://www.mysql.com/downloads/mysql/ 端口号:3306 用户名:root 密码:自定义 连接到MySQL服务器 >mysql -uroot -pr ...
- Web Api 过滤器之 AuthorizationFilter 验证过滤器
该过滤器是最先执行的过滤器,即使把它放在最后 API [MyActionFilter] [MyExceptionFilter] [MyAuthorize] public void Get() { Tr ...
- Django实现 省 市 县 自关联的下拉级联
前端部分: 三个下拉拉菜单进行级联 <body> <select id="province" > <option value="" ...
- oracle获取表字段属性
select b.COMMENTS,a.COLUMN_NAME,a.DATA_TYPE,a.DATA_LENGTH, a.DATA_PRECISION,a.DATA_SCALE,a.NULLABLE, ...
- python--socket粘包
socket粘包 1 什么是粘包 须知:只有TCP有粘包现象,UDP永远不会粘包,首先需要掌握一个socket收发消息的原理, 所谓粘包问题主要还是因为接收方不知道消息之间的界限,不知道一次性提取多少 ...
- kafka_2.12-1.1.0 生产与消费java实现示例
环境准备: 1)需要在maven工程中引入依赖: <!-- https://mvnrepository.com/artifact/org.apache.kafka/kafka --> &l ...
- Hibernate(十三):HQL查询(二)
背景 基于上一章节<Hibernate(十二):HQL查询(一)>,已经学习了一部分关于HQL的用法: HQL带参数查询 HQL Order By排序查询 HQL 设置实体参数查询 本章节 ...
- Hibernate(四):Hello World
下载hibernate开发包: 在本章之前需要继承hibernate开发插件到eclipse,详细操作请参考我的博文:<Hibernate(一):安装hibernate插件到eclipse环境& ...
- Hibernate(二):MySQL server version for the right syntax to use near 'type=InnoDB' at line x
目前使用的hibernate5.2.9版本,配置的mysql方言为: <property name="hibernate.dialect">org.hibernate. ...
