POJ 2007 Scrambled Polygon [凸包 极角排序]

Scrambled Polygon

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 8636		Accepted: 4105

Description

A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.

A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn't have any "dents".)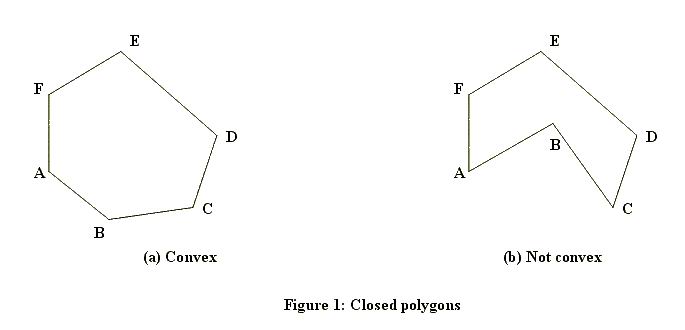 

The subject of this problem is a closed convex polygon in the coordinate plane, one of whose vertices is the origin (x = 0, y = 0). Figure 2 shows an example. Such a polygon will have two properties significant for this problem.

The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).

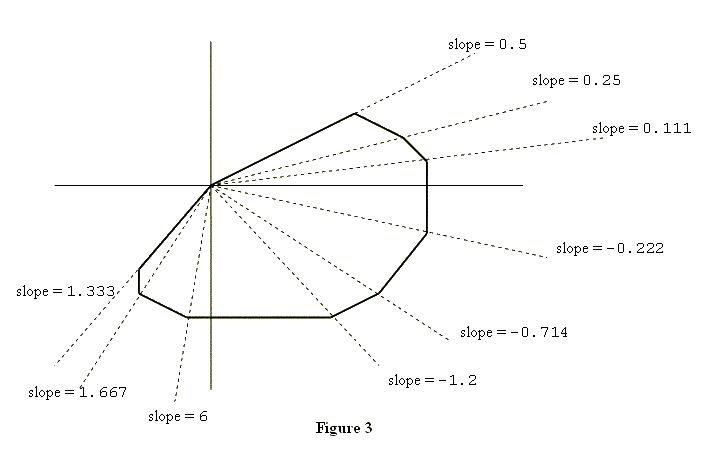
To describe the second property, suppose you "take a trip" around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.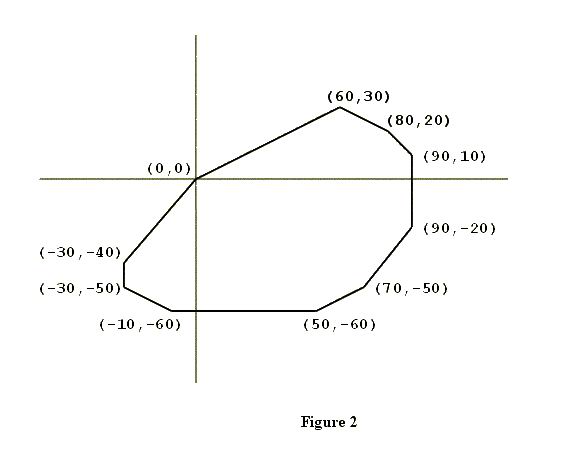 
 

Input

The input lists the vertices of a closed convex polygon in the plane. The number of lines in the input will be at least three but no more than 50. Each line contains the x and y coordinates of one vertex. Each x and y coordinate is an integer in the range -999..999. The vertex on the first line of the input file will be the origin, i.e., x = 0 and y = 0. Otherwise, the vertices may be in a scrambled order. Except for the origin, no vertex will be on the x-axis or the y-axis. No three vertices are colinear. 

Output

The output lists the vertices of the given polygon, one vertex per line. Each vertex from the input appears exactly once in the output. The origin (0,0) is the vertex on the first line of the output. The order of vertices in the output will determine a trip taken along the polygon's border, in the counterclockwise direction. The output format for each vertex is (x,y) as shown below. 

Sample Input

0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10

Sample Output

(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)

Source

Rocky Mountain 2004

---

显然极角排序 用叉积 但WA好多次最后发现必须要保证第一个点在开始，排序直接跳过就行了

或者强行用凸包做也可以，因为凸包结束后就是极角拍好序的了

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=;
const double eps=1e-;

inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}

inline int sgn(double x){
    if(abs(x)<eps) return ;
    else return x<?-:;
}

struct Vector{
    double x,y;
    Vector(double a=,double b=):x(a),y(b){}
};
typedef Vector Point;
double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}

int n,x,y;
Point p[N],S;
bool cmpPolar(Point a,Point b){
    return sgn(Cross(a,b))>;
}
int main(int argc, const char * argv[]) {
    while(scanf("%d",&x)!=EOF){
        y=read();
        p[++n]=Point(x,y);
    }
    sort(p+,p++n,cmpPolar);
    for(int i=;i<=n;i++) printf("(%.0f,%.0f)\n",p[i].x,p[i].y);
    return ;
}

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
typedef long long ll;
const int N=;
const double eps=1e-;
const double pi=acos(-);

inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}

inline int sgn(double x){
    if(abs(x)<eps) return ;
    else return x<?-:;
}

struct Vector{
    double x,y;
    Vector(double a=,double b=):x(a),y(b){}
    bool operator <(const Vector &a)const{
        //return x<a.x||(x==a.x&&y<a.y);
        return sgn(x-a.x)<||(sgn(x-a.x)==&&sgn(y-a.y)<);
    }
};
typedef Vector Point;
Vector operator +(Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}
Vector operator -(Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator *(Vector a,double b){return Vector(a.x*b,a.y*b);}
Vector operator /(Vector a,double b){return Vector(a.x/b,a.y/b);}
bool operator ==(Vector a,Vector b){return sgn(a.x-b.x)==&&sgn(a.y-b.y)==;}

double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}
double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}
double DisPP(Point a,Point b){
    Point t=b-a;
    return sqrt(t.x*t.x+t.y*t.y);
}
int ConvexHull(Point p[],int n,Point ch[]){//cannot handle repeat point
    sort(p+,p++n);
    int m=;
    for(int i=;i<=n;i++){
        while(m>&&sgn(Cross(ch[m]-ch[m-],p[i]-ch[m-]))<=) m--;
        ch[++m]=p[i];
    }
    int k=m;
    for(int i=n-;i>=;i--){
        while(m>k&&sgn(Cross(ch[m]-ch[m-],p[i]-ch[m-]))<=) m--;
        ch[++m]=p[i];
    }
    if(n>) m--;//the first point
    return m;
}
int n,x,y;
double ans;
Point p[N],ch[N];
int main(int argc, const char * argv[]) {
    while(scanf("%d",&x)!=EOF){
        y=read();
        p[++n]=Point(x,y);
    }
    ConvexHull(p,n,ch);
    Point S(,);int p;
    for(p=;p<=n;p++) if(ch[p]==S) break;

    for(int i=p;i<=n;i++) printf("(%.0f,%.0f)\n",ch[i].x,ch[i].y);
    for(int i=;i<p;i++) printf("(%.0f,%.0f)\n",ch[i].x,ch[i].y);
    return ;
}