编译原理：非确定的自动机NFA确定化为DFA

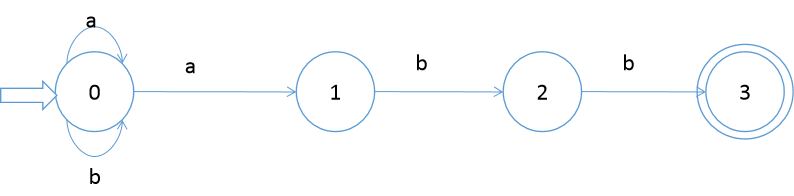
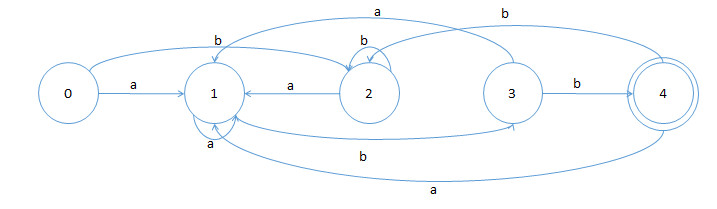
1.设有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} )，其中 f(0,a)={0,1}  f(0,b)={0}  f(1,b)={2}  f(2,b)={3}

画出状态转换矩阵,状态转换图，并说明该NFA识别的是什么样的语言。

解析：

	a	b
0	{0,1}	0
1		2
2		3
3

状态转换图如下：

　　　　　　　　　　　　　　　　　　　　　　

识别语言为：(a | b)*abb

2.NFA 确定化为 DFA

1.解决多值映射：子集法

1）. 上述练习1的NFA

解析：

根据1的NFA构造DFA状态转换矩阵如下：

		a	b
A	{0}	{0,1}	{0}
B	{0,1}	{0,1}	{0,2}
C	{0,2}	{0,1}	{0,3}
D	{0,3}	{0,1}	{0}

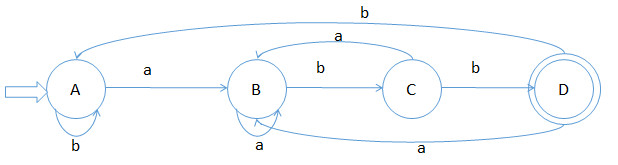
　　根据1的NFA构造DFA状态转换图如下：

　　

　　识别语言：b*aa*(ba)*bb， 与1的NFA的识别的语言相同，都是以abb结尾的字符串的集合。

2）. P64页练习3

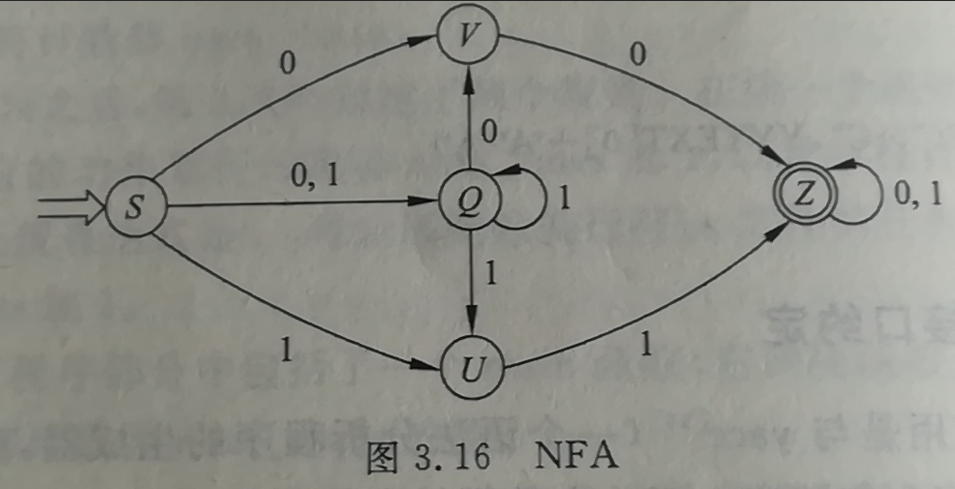
状态转换矩阵如下：

		0	1
A	{S}	{Q,V}	{Q,U}
B	{Q,V}	{V,Z}	{Q,U}
C	{V,Z}	{Z}	{Z}
D	{Q,U}	{V}	{Q,U,Z}
E	{V}	{Z}
F	{Q,U,Z}	{V,Z}	{Q,U,Z}
G	{Z}	{Z}	{Z}

状态转换图如下：

　　　　　　　　　　　　　　　　　　　　　　　　　　

2.解决空弧：对初态和所有新状态求ε－闭包

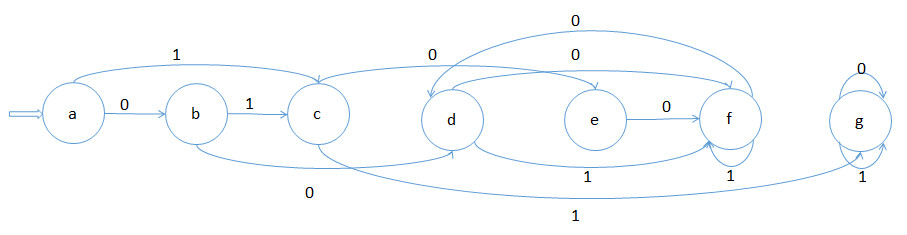
1）. 发给大家的图2

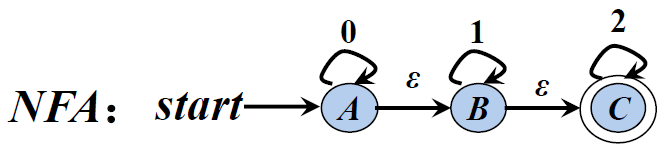
解析：

识别语言：0*(11*2 | 2)2*

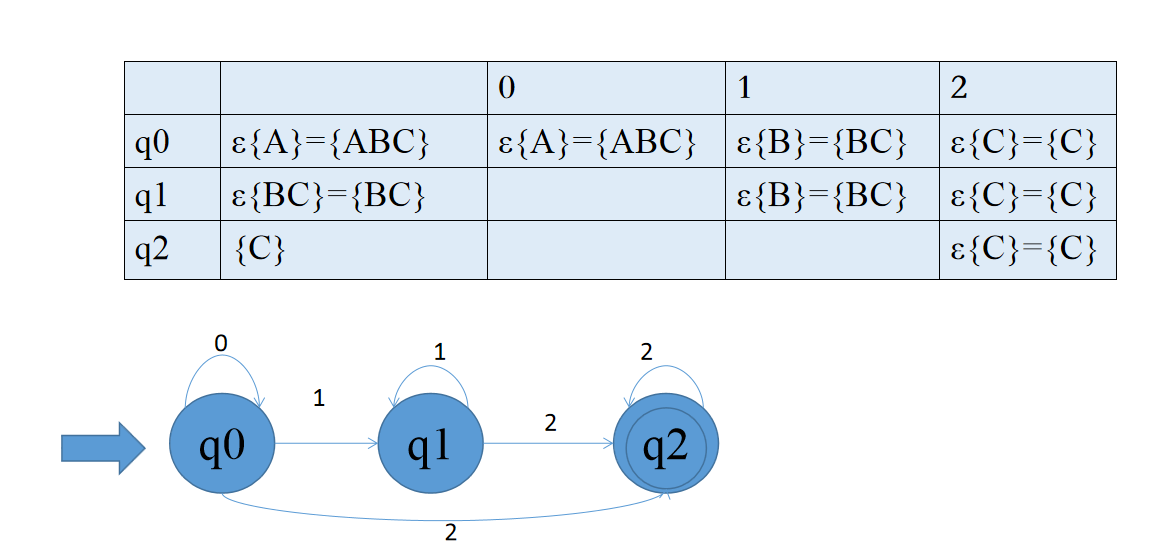
2）.P50图3.6

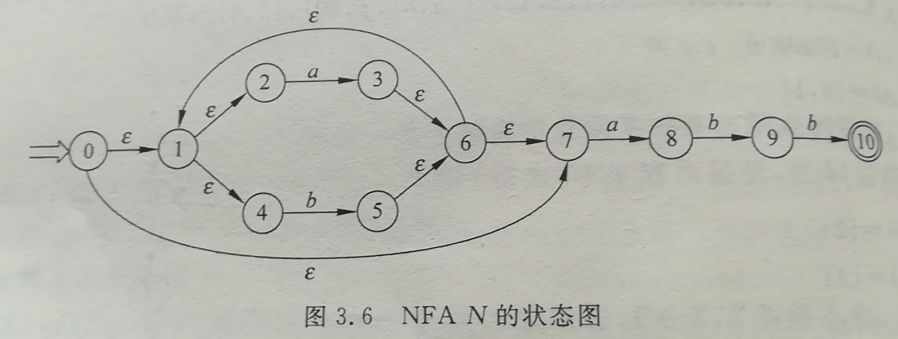
子集法：

f(q,a)={q1,q2,…,qn},状态集的子集

将{q1,q2,…,qn}看做一个状态A，去记录NFA读入输入符号之后可能达到的所有状态的集合。

步骤：

1）.根据NFA构造DFA状态转换矩阵

①确定DFA的字母表，初态（NFA的所有初态集）

②从初态出发，经字母表到达的状态集看成一个新状态

③将新状态添加到DFA状态集

④重复23步骤，直到没有新的DFA状态

2）.画出DFA

3）.看NFA和DFA识别的符号串是否一致。

解析：

 识别语言：(a | bb*a)a*(ba)*bb((bb*aa*(ba)*bb)* | (aa*(ba)*bb)*)