长脖子鹿放置【洛谷P5030】二分图最大独立集变形题

题目背景

众周所知，在西洋棋中，我们有城堡、骑士、皇后、主教和长脖子鹿。

题目描述

如图所示，西洋棋的“长脖子鹿”，类似于中国象棋的马，但按照“目”字攻击，且没有中国象棋“别马腿”的规则。（因为长脖子鹿没有马腿）

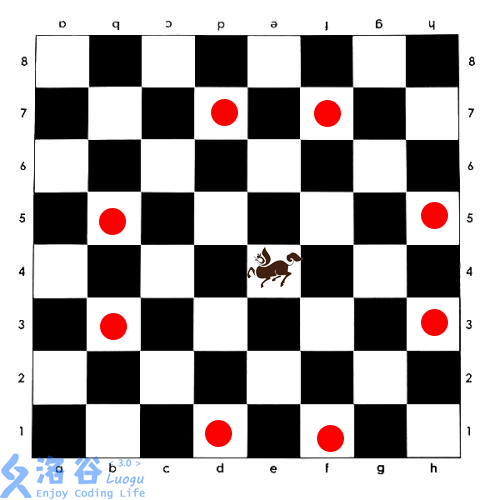
给定一个N * MN∗M,的棋盘，有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。

输入格式

输入的第一行为两个正整数NN，MM，KK。其中KK表示禁止放置长脖子鹿的格子数。

第22~第K+1K+1行每一行为两个整数Xi, YiXi,Yi,表示禁止放置的格子。

输出格式

一行一个正整数，表示最多能放置的长脖子鹿个数。

输入输出样例

输入 #1复制

2 2 1
1 1

输出 #1复制

3

输入 #2复制

/*额外提供一组数据*/
8 7 5
1 1
5 4
2 3
4 7
8 3

输出 #2复制

28
思路：

• 首先我们看，在棋盘上放棋子，让他们互相不能攻击，这明显是到二分图最大独立集（类似题骑士共存问题）

• 接着我们想怎样染色，第一下想的就是像棋盘那样按行列奇偶性来染，但是显然不对。于是我们发现一个惊人的问题，基数行和偶数行之间的棋子不会互相攻击！！！这样就好了，按行奇偶性来染色，跑个二分图最大独立集就行（二分图最大独立集=点数-最大匹配数）

80分的代码QAQ：

 #include<bits/stdc++.h>

 //最大独立集=n-最小点覆盖
 using namespace std;
 #define maxn 6666
 int dx[]={,,,,-,-,-,-};
 int dy[]={,-,,-,,-,,-};
 int mp[maxn][maxn];
 int match[*];
 int vis[];
 int num[maxn][maxn];
 int flag=;
 int n,m,k;
 int head[maxn*maxn];
 inline int read(){
     char c = getchar(); int x = , f = ;
     while(c < '' || c > '') {if(c == '-') f = -; c = getchar();}
     while(c >= '' & c <= '') x = x *  + c - '', c = getchar();
     return x * f;
 }
 struct Edge{
     int to,next;
 }e[**];
 void  add(int u,int v){
     flag++;
     e[flag].to=v;
     e[flag].next=head[u];
     head[u]=flag;
 }
 inline int cal_note(int xx,int yy){    //计算该格子的编号
     return (xx-)*n+yy;
 }
 int dfs(int u){
     for(register int i=head[u];i;i=e[i].next){
         int temp=e[i].to;
         if(!vis[temp]){
             vis[temp]=;
             if(match[temp]==||dfs(match[temp]))
             {
                 match[temp]=u;
                 return ;
             }
         }
     }
     return ;
 }
 int main(){
     //int n,m;
     //scanf("%d%d",&n,&m);
     n=read();
     m=read();
     k=read();
     int xx,yy;
     for(int i=;i<=k;i++){
         //scanf("%d%d",&x,&y);
         xx=read();
         yy=read();
         mp[xx][yy]=;// 标记不可以走到的点
     }
     int cnt=;
     /*for(int i=1;i<=n;i++)
         for(int j=1;j<=m;j++)
             num[i][j]=++cnt;        // 给每一个点编号 */
     for(register int i=;i<=n;i+=){
         for(register int j=;j<=m;j++){
             if(mp[i][j])
                 continue;
             else{
                 int x=i;
                 int y=j;
                 for(int k=;k<;k++){
                     int tx=x+dx[k];
                     int ty=y+dy[k];
                     if(tx>=&&ty>=&&tx<=n&&ty<=m&&!mp[tx][ty]){
                         //v[num[x][y]].push_back(num[tx][ty]);
                         //v[num[tx][ty]].push_back(num[x][y]);
                         add(cal_note(i,j),cal_note(tx,ty));
                     //    add(cal_note(tx,ty),cal_note(x,y));
                     }
                 }
             }
         }
     }
     int ans=;
     for(register int i=;i<=n;i+=){
         for(register int j=;j<=m;j++){
             if(mp[i][j])
                 continue;
             memset(vis,,sizeof(vis));
             if(dfs(cal_note(i,j)))
                 ans++;
         }
     }
     int res=n*m-k-ans;
     printf("%d\n",res);
     return ;
 }