Liang-Barsky算法

Liang-Barsky算法

在Cohen-Sutherland算法提出后，梁友栋和Barsky又针对标准矩形窗口提出了更快的Liang-Barsky直线段裁剪算法。

梁算法的主要思想：

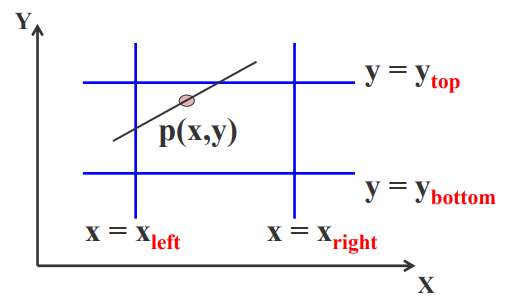
（1）用参数方程表示一条直线

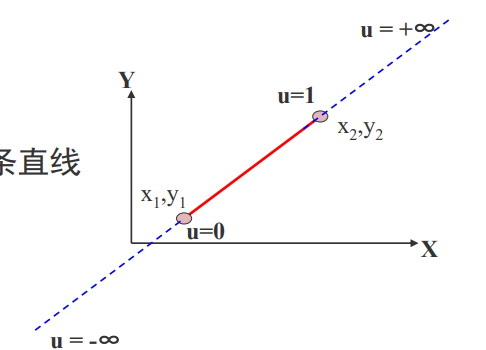
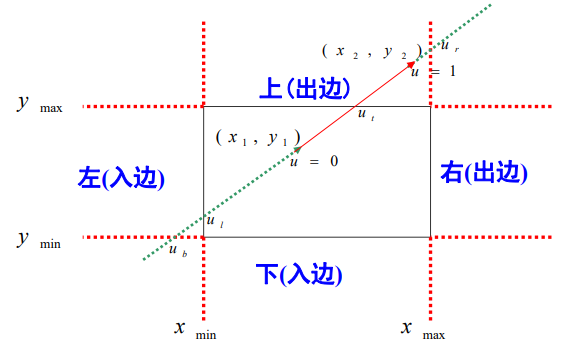
（2）把被裁剪的红色直线段看 成是一条有方向的线段，把窗口 的四条边分成两类：

入边和出边

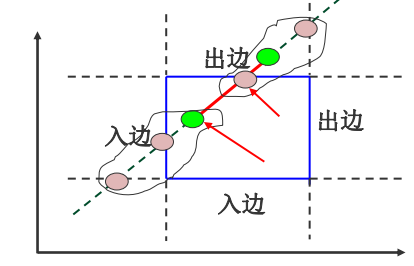
裁剪结果的线段起点是直线和两条入边的交点以及始端点三 个点里最前面的一个点，即参数u最大的那个点；

裁剪线段的终点是和两条出边的交点以及端点最后面的一个 点，取参数u最小的那个点。

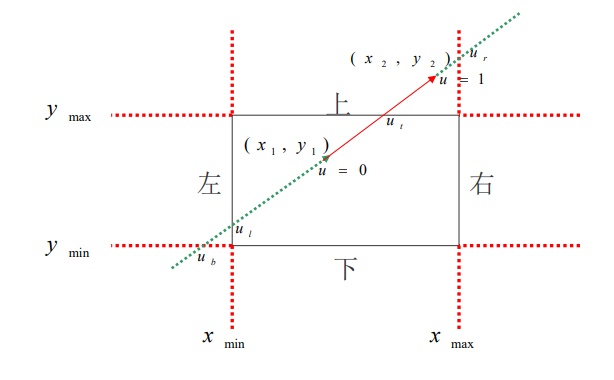
值得注意的是，当u从-∞到+∞遍历直线时，首先对裁剪窗口的两条边界直线（下边和左边）从外面向里面移动，

再对裁 剪窗口两条边界直线（上边和右边）从里面向外面移动。

如果用u1，u2分别表示 线段（u1≤u2）可见部分的开始和结束

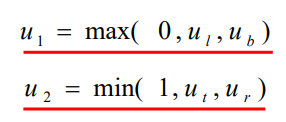
Liang-Barsky算法的基本出发点是直线的参数方程

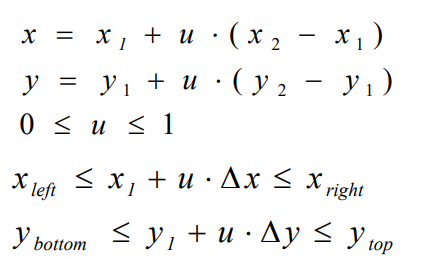
（1）分析Pk=0的情况

如果还满足qk<0

则线段完全在边界外，应舍 弃该线段

如果qk≥0

则进一步判断

（2）当pk≠0时：

当pk<0时

线段从裁剪边界延长线的外部 延伸到内部，是入边交点

当pk > 0时

线段从裁剪边界延长线的内部 延伸到外部，是出边交点

线段和窗口边界一共有四个交点，根据pk的符号，就知道 哪两个是入交点，哪两个是出交点

当p k < 0时：对应入边交点

当p k > 0时：对应出边交点

一共四个u值，再加上u=0、u=1两个端点值，总共六个值

把pk＜0的两个u值和0比较去找最大的，把pk＞0的两个u值 和1比较去找最小的，这样就得到两个端点的参数值