Blocks(POJ 3734)

• 原题如下：
  Blocks

  Time Limit: 1000MS		Memory Limit: 65536K
  Total Submissions: 8020		Accepted: 3905

  Description

  Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent boy, he starts to think of a math problem of painting. Suppose there are N blocks in a line and each block can be paint red, blue, green or yellow. For some myterious reasons, Panda want both the number of red blocks and green blocks to be even numbers. Under such conditions, Panda wants to know the number of different ways to paint these blocks.

  Input

  The first line of the input contains an integer T(1≤T≤100), the number of test cases. Each of the next T lines contains an integer N(1≤N≤10^9) indicating the number of blocks.

  Output

  For each test cases, output the number of ways to paint the blocks in a single line. Since the answer may be quite large, you have to module it by 10007.

  Sample Input

  2
  1
  2

  Sample Output

  2
  6

• 题解：从最左边开始染色，设染到第i个方块为止，红绿都是偶数的方案数为a_i，红绿恰有一个是偶数的方案数为b_i，红绿都是奇数的方案数为c_i。这样，染到第i+1个方块为止，红绿都是偶数的方案数有两种可能：①到第i个方块为止红绿都是偶数，并且第i+1个方块染成了蓝色或者黄色 ② 到第i个方块为止红绿恰有一个是奇数， 并且第i+1个方块染成了奇数个对应的那种颜色。因此有递推式a_i+1=2*a_i+b_i，同样地，有b_i+1=2*a_i+2*b_i+2*c_i，c_i+1=b_i+2*c_i，把a_i，b_i，c_i的递推式用矩阵表示如下：
  

  因此就有：
  

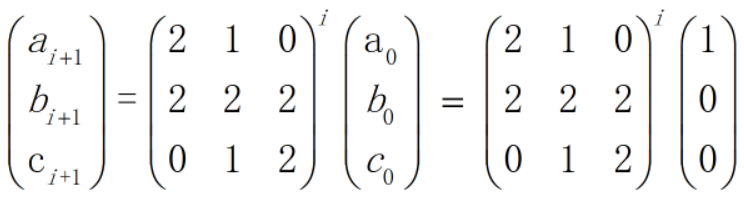
• 代码：

   #include <cstdio>
   #include <cctype>
   #define number s-'0'
   #include <cstring>
   #include <vector>
  
   using namespace std;
  
   typedef vector<int> vec;
   typedef    vector<vec> mat;
  
   const int M=;
   int N;
  
   void read(int &x)
   {
       char s;
       x=;
       bool flag=;
       while (!isdigit(s=getchar()))
           (s=='-')&&(flag=true);
       for (x=number; isdigit(s=getchar());x=x*+number);
       (flag)&&(x=-x);
   }
  
   void write(int x)
   {
       if (x<)
       {
           putchar('-');
           x=-x;
       }
       if (x>) write(x/);
       putchar(x%+'');
   }
  
   mat mul(mat &A, mat &B)
   {
       mat C(A.size(), vec(B[].size()));
       for (int i=; i<A.size(); i++)
       {
           for (int j=; j<B[].size(); j++)
           {
               for (int k=; k<B.size(); k++)
               {
                   C[i][j]=(C[i][j]+A[i][k]*B[k][j])%M;
               }
           }
       }
       return C;
   }
  
   mat pow(mat A, int n)
   {
       mat B(A.size(), vec(A.size()));
       for (int i=; i<A.size(); i++) B[i][i]=;
       while (n>)
       {
           if (n&) B=mul(B, A);
           A=mul(A, A);
           n>>=;
       }
       return B;
   }
  
   int main(int argc, char * argv[])
   {
       int t;
       read(t);
       while (t>)
       {
           t--;
           read(N);
           mat A(, vec());
           A[][]=;A[][]=;A[][]=;
           A[][]=;A[][]=;A[][]=;
           A[][]=;A[][]=;A[][]=;
           A=pow(A, N);
           printf("%d\n",A[][]);
       }
   }