logistic regression中的cost function选择

一般的线性回归使用的cost function为:

但由于logistic function：

本身非凸函数（convex function）， 如果直接使用线性回归的cost function的话，很难到达全局最优解。

相反，很容易陷入局部最优解然后就认为到达收敛条件了。因此，logistic regression中使用的cost function为：

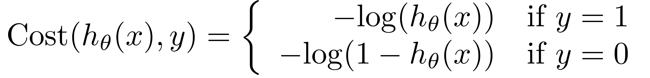
其图像为一个碗（bowl shape function），碗的底部为（1,0）。可以看出：当预测正确且非常自信时（h（x) = y），

cost function 为0； 当完全预测错误且非常自信时（h(x) = !y）, cost function 为 inf。