P4716 【模板】最小树形图

题意

说一下我对朱刘算法的理解：

首先我们考虑树形图的性质：每个点除了根节以外都含有一条入边。

因此我们可以有一个贪心的想法：对每个点（除了根节点）找到一条最短的入边，但是这样会出现环，如下图：



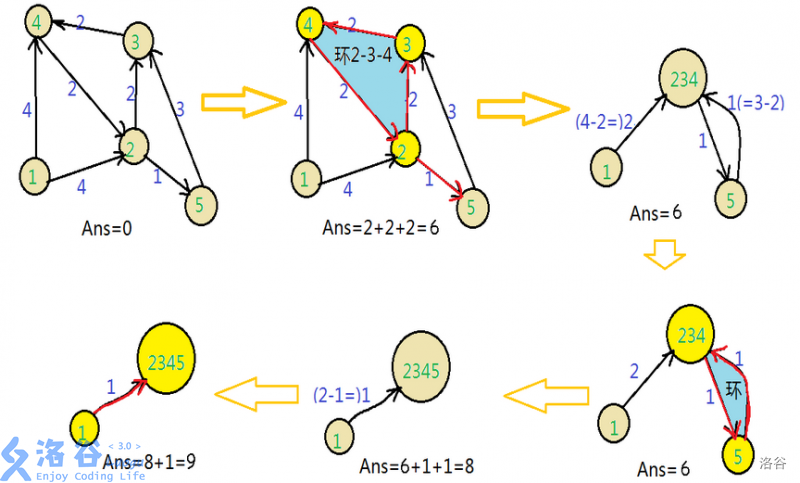
我们会找到\(2-3-4\)这个环。

根据贪心的思想，我们最终的答案必定含有这个环去掉一条边，于是我们将这三个点缩成一个点，加上这三条边的答案，并且修改所有连向这三个点的边的边权。

举个例子：

原来有条边\(1->4\)，边权为\(4\)，连向\(4\)的最小边权为\(2\)，我们已经加上了\(2\)，因此如果再选\(1->4\)，那么应该再加上\(4-2=2\)，于是这条边的边权改为\(2\)。

我们不断迭代，复杂度为\(O(nm)\)。

code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=110;
const int maxm=1e4+10;
const int inf=1e9;
int n,m,root;
int fa[maxn],pre[maxn],mindis[maxn],col[maxn];
struct Edge{int u,v,w;}E[maxm];
inline ll solve()
{
	ll res=0;
	while(2333)
	{
		int cnt=0;
		for(int i=1;i<=n;i++)fa[i]=pre[i]=col[i]=0,mindis[i]=inf;
		for(int i=1;i<=m;i++)
			if(E[i].u!=E[i].v&&mindis[E[i].v]>E[i].w)
				pre[E[i].v]=E[i].u,mindis[E[i].v]=E[i].w;
		mindis[root]=0;
		for(int i=1;i<=n;i++)
		{
			if(mindis[i]==inf)return -1;
			res+=mindis[i];
			int x=i;
			while(x!=root&&fa[x]!=i&&!col[x])fa[x]=i,x=pre[x];
			if(x!=root&&!col[x])
			{
				col[x]=++cnt;
				int y=pre[x];
				while(y!=x)col[y]=cnt,y=pre[y];
			}
		}
		if(!cnt)return res;
		for(int i=1;i<=n;i++)if(!col[i])col[i]=++cnt;
		for(int i=1;i<=m;i++)
		{
			int delta=mindis[E[i].v];
			E[i].u=col[E[i].u],E[i].v=col[E[i].v];
			if(E[i].u!=E[i].v)E[i].w-=delta;
		}
		n=cnt;root=col[root];
	}
	return 233;
}
int main()
{
	scanf("%d%d%d",&n,&m,&root);
	for(int i=1;i<=m;i++)scanf("%d%d%d",&E[i].u,&E[i].v,&E[i].w);
	printf("%lld",solve());
	return 0;
}