BZOJ 4005 [JLOI 2015] 骗我呢

首先，我们可以得到：每一行的数都是互不相同的，所以每一行都会有且仅有一个在 $[0, m]$ 的数没有出现。

我们可以考虑设 $Dp[i][j]$ 为处理完倒数 $i$ 行，倒数第 $i$ 行缺的数字是 $j$ 的方案数。

那么就有：

$$Dp[i][j] = \sum_{k=max(0,j-1)}^{m}Dp[i - 1][k]$$

自己画一画图就可以明白了，在这里就不解释了。毕竟 Gromah 太懒($ru\grave{o}$)

然后我们考虑把这个转移图画出来：

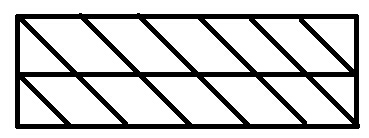
然后就是求这个图中从右上到左下的路径条数嘛。（每次只能往左或者是往右下或者是往下）

转化一下，实际上就是求这个东西：

从 $(0,0)$ 到 $(n*2+m+1,m+1)$，每次可以 $x+1,y-1$ 或者 $x+1,y+1$，并且不穿过 $y=0$ 和 $y=m+1$ 这两条直线的路径条数。

首先，全集是 ${n*2+m+1 \choose m+1}$，

然后我们算穿过 $y=0$ 的路径条数，既然穿过 $y=0$ 就必然经过 $y=-1$，于是我们让终点和 $y=m+2$ 这条直线沿着 $y=-1$ 翻转，

然后就可以算出 $(0,0)$ 到翻转之后的终点的路径条数。

于是还没完。还有那些先穿过 $y=0$ 再又穿过 $y=m+1$ 这条直线的路径我们要加回来。。。

于是又把坐标系沿着翻转之后的 $y=m+2$ （此时应该是 $y=-m-4$ 了）再次翻转。再统计答案。。。

直到方案为 $0$ 了为止。

计算穿过 $y=m+1$ 的路径条数同理。。。

我知道我语言表达能力及其低下，所以还是上代码好了。。。

 #include <cmath>
 #include <cstdio>
 #include <cstring>
 #include <iostream>
 #include <algorithm>
 using namespace std;
 typedef long long LL;
 #define N 3000000
 #define Mod 1000000007

 int n, m, ans = ;
 int Fac[N + ], Inv[N + ];

 inline int power(int u, int v)
 {
     int res = ;
     for (; v; v >>= )
     {
         if (v & ) res = (LL) res * u % Mod;
         u = (LL) u * u % Mod;
     }
     return res;
 }

 inline void Prepare()
 {
     Fac[] = Inv[] = ;
     for (int i = ; i <= N; i ++)
         Fac[i] = (LL) Fac[i - ] * i % Mod;
     Inv[N] = power(Fac[N], Mod - );
     for (int i = N - ; i ; i --)
         Inv[i] = (LL) Inv[i + ] * (i + ) % Mod;
 }

 inline int C(int u, int v)
 {
     if (u <  || v <  || u < v) return ;
     return (LL) Fac[u] * Inv[v] % Mod * Inv[u - v] % Mod;
 }

 inline int T(int u, int v)
 {
     if (u < abs(v)) return ;
     return C(u, u - abs(v) >> );
 }

 inline int Inc(int u, int v)
 {
     return u + v - (u + v >= Mod ? Mod : );
 }

 int main()
 {
     #ifndef ONLINE_JUDGE
         freopen("4005.in", "r", stdin);
         freopen("4005.out", "w", stdout);
     #endif

     Prepare();
     scanf("%d%d", &n, &m);
     int x = n *  + m + ;
     ans = T(x, m + );

     for (int y = m + , y_1 = -, y_2 = m + ; x >= abs(y); )
     {
         y =  * y_1 - y;
         y_2 =  * y_1 - y_2;
         ans = Inc(ans, Mod - T(x, y));
         y =  * y_2 - y;
         y_1 =  * y_2 - y_1;
         ans = Inc(ans, T(x, y));
     }

     for (int y = m + , y_1 = m + , y_2 = -; x >= abs(y); )
     {
         y =  * y_1 - y;
         y_2 =  * y_1 - y_2;
         ans = Inc(ans, Mod - T(x, y));
         y =  * y_2 - y;
         y_1 =  * y_2 - y_1;
         ans = Inc(ans, T(x, y));
     }

     printf("%d\n", ans);

     #ifndef ONLINE_JUDGE
         fclose(stdin);
         fclose(stdout);
     #endif
     return ;
 }

4005_Gromah