ubuntu之路——day10.6 如何理解人类表现和超过人类表现
从某种角度来说,已知的人类最佳表现其实可以被当做贝叶斯最优错误,对于医学图像分类可以参见下图中的例子。
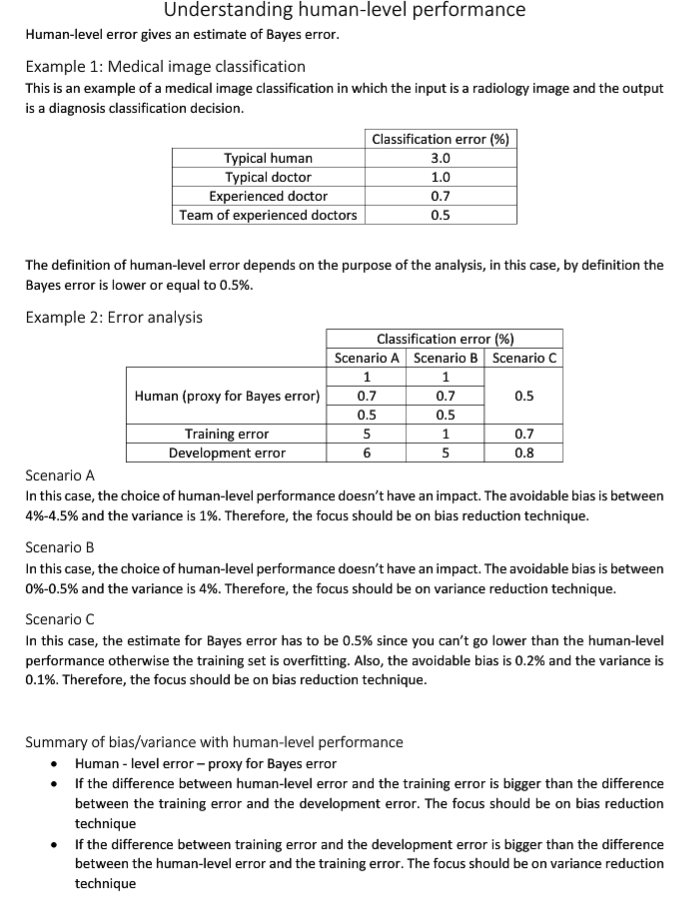
那么如何理解超过人类表现,在哪些领域机器已经做到了超越人类呢?

ubuntu之路——day10.6 如何理解人类表现和超过人类表现的更多相关文章
- ubuntu之路——day10.4 什么是人的表现
结合吴恩达老师前面的讲解,可以得出一个结论: 在机器学习的早期阶段,传统的机器学习算法在没有赶超人类能力的时候,很难比较这些经典算法的好坏.也许在不同的数据场景下,不同的ML算法有着不同的表现. 但是 ...
- ubuntu之路——day10.7 提高模型的表现
总结一下就是在提升偏差的方面(即贝叶斯最优误差和训练误差的差距) 1.尝试更大更深的网络 2.加入优化算法比如前面提过的momentum.RMSprop.Adam等 3.使用别的神经网络架构比如RNN ...
- ubuntu之路——day10.5 可避免偏差
可避免偏差: 总结一下就是当贝叶斯最优误差接近于训练误差的时候,比如下面的例子B,我们不会说我们的训练误差是8%,我们会说我可避免偏差是0.5%.
- ubuntu之路——day10.3 train/dev/test的划分、大小和指标更新
train/dev/test的划分 我们在前面的博文中已经提到了train/dev/test的相关做法.比如不能将dev和test混为一谈.同时要保证数据集的同分布等. 现在在train/dev/t ...
- ubuntu之路——day10.2单一数字评估指标与满足和优化的评估指标
单一数字评估指标: 我们在平时常用到的模型评估指标是精度(accuracy)和错误率(error rate),错误率是:分类错误的样本数站样本总数的比例,即E=n/m(如果在m个样本中有n个样本分类错 ...
- ubuntu之路——day10.1 ML的整体策略——正交化
orthogonalization 正交化的概念就是指,将你可以调整的参数设置在不同的正交的维度上,调整其中一个参数,不会或几乎不会影响其他维度上的参数变化,这样在机器学习项目中,可以让你更容易更快速 ...
- Python之路,Day10 - 异步IO\数据库\队列\缓存
Python之路,Day9 - 异步IO\数据库\队列\缓存 本节内容 Gevent协程 Select\Poll\Epoll异步IO与事件驱动 Python连接Mysql数据库操作 RabbitM ...
- python之路-Day10
操作系统发展史介绍 进程.与线程区别 python GIL全局解释器锁 线程 语法 join 线程锁之Lock\Rlock\信号量 将线程变为守护进程 Event事件 queue队列 生产者消费者模型 ...
- python学习之路-day10
一.什么是线程 在传统操作系统中,每个进程有一个地址空间,而且默认就有一个控制线程. 线程顾名思义,就是一条流水线工作的过程,一条流水线必须属于一个车间,一个车间的工作过程是一个进程. 车间负责把资源 ...
随机推荐
- 【阅读笔记:散列表】Javascript任何对象都是一个散列表(hash表)!
什么是散列表? 散列表是Dictionary(字典)的一种散列表实现方式,字典传送门 一个很常见的应用是使用散列表来表示对象.Javascript语言内部就是使用散列表来表示每个对象.此时,对象的每个 ...
- spring boot 简要常用配置
# 激活开发环境 spring.profiles.active=dev spring.mvc.date-format=yyyy-MM-dd HH:mm:ss spring.http.encoding. ...
- MySQL DataType--当整数列遇到小数
初始化数据: ## 创建测试表 CREATE TABLE `tb002` ( `c1` ) NOT NULL AUTO_INCREMENT, `c2` ) DEFAULT NULL, `c3` ) D ...
- python(类的封装调用/继承/多态)
一.类的定义 类:用来描述具有相同的属性和方法的对象的集合.它定义了该集合中每个对象所共有的属性和方法.对象是类的实例 对象:类实例化出来的叫做对象 对象和类的关系:类和对象的关系就像模具和铸 ...
- Python——模块合集
标准库模块 ● Python——OS(系统操作模块) ● Python——MD5(加密模块) ● Python——time(时间模块) ● Python——re(正则表达式) ● Python——sy ...
- windows的bpython安装方法以及数据库报错--记录
---恢复内容开始--- 安装bpython的时候发现了一个博客讲解如何成功安装bpython,分享一下链接http://www.cnblogs.com/zhaojiedi1992/p/zhaojie ...
- [ipsec][strongswan] strongswan源码分析-- (二)rekey/reauth机制分析
目录 strongwan sa分析(二) 名词约定 rekey/reauth 机制分析 1 概述 2 reauth 3 CHILD SA rekey 4 IKE SA rekey 5 其他 stron ...
- lvm快照备份mysql
快照备份原理(从其他博客看的): 原理:通过lvm快照给lvm真身拍个照片,当lvm真身发送改变时,lvm快照把lvm真身改变之前的内容存放在快照上,这样在lvm快照有效的这段时间内,我们看到的lvm ...
- web 错误代码解析
404表示文件或资源未找到java WEB常见的错误代码1.1xx-信息提示:这些状态代码表示临时的响应.客户端在收到常规响应之前,应准备接收一个或多个1xx响应.100-继续.101-切换协议.2. ...
- 网站检测空链、死链工具(Xenu)
网站常用检测空链.死链工具,Xenu是很小但是功能强大的检查网站404链接的软件,支持多线程,无需安装可直接打开使用.步骤如下: 网站的链接一般都成千上万,如果存在大量的空链接将大大的影响用户体验,怎 ...
