DS 图解堆排

　　　　　　堆排其实就是选择排序,只不过用了完全二叉树特性。

　　　　　　堆排思想 : 利用完全二叉树特性建堆和重复选择调整来得到有序数组。

　　　　　　完全二叉树有什么特性呢? 节点左对齐 ---> 层序遍历不会出现空,可以用数组表达(访问效率高)

　　　　　　那么可以将它映射到数组上,并且遵循一个规律: 设i为当前节点索引,

　　　　　    i->left = 2*i+1              i->right = 2*i+2   可得-->

　　　　　　i = (i->left-1)/2 = (i->right-2)/2  = (i->left-2 +1)/2 = (i->left-2)/2 + 1/2(计算机整除为0) = (i->child-1)/2

　　　　   

　　

　　　　　堆排序种类:

　　　　　  大根堆 : parent > left && right   ---> 升序

　　　　　  小根堆 : parent < left && right   ---> 降序

　　　　　  堆排序最经典的问题就是topK问题。

　　　　　　

　　　　　　堆排过程(假如要降序) :

　　　　　　1. 建小堆    

　　　　             　　

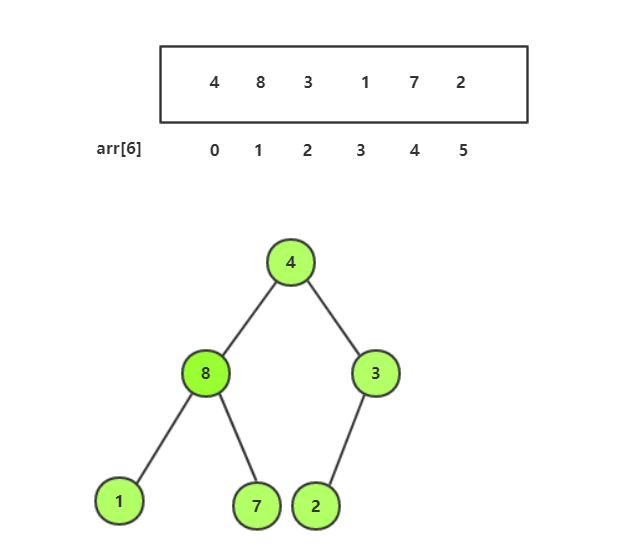
　　　　　　　　　　　　  建小堆过程:  1.找到最后一个非叶子节点(叶子节点不用调整,因为向下调整前提是有孩子),进行向下调整 

　　　　　　　　　　　　　　　　　　   2.依次向前将所有非叶子节点调整完,小堆也就构建好了

　　　　　　　　　　　  　1.选最后一个非叶子节点 3,向下调整

　　　　　　　　　　　　

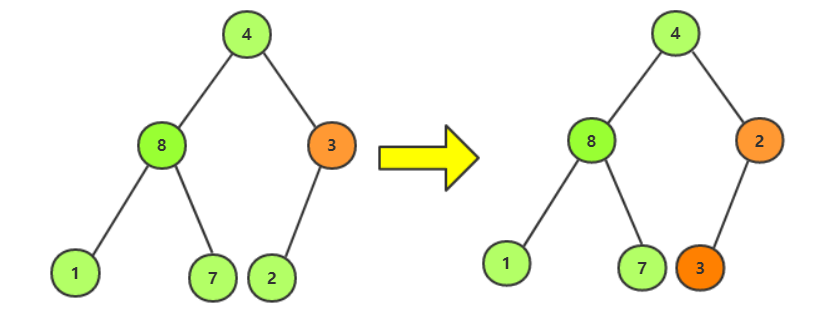
　　　　　　　　　　　     2.继续找倒数第二个非叶子节点向下调整,重复直到全部非叶子节点调整完成

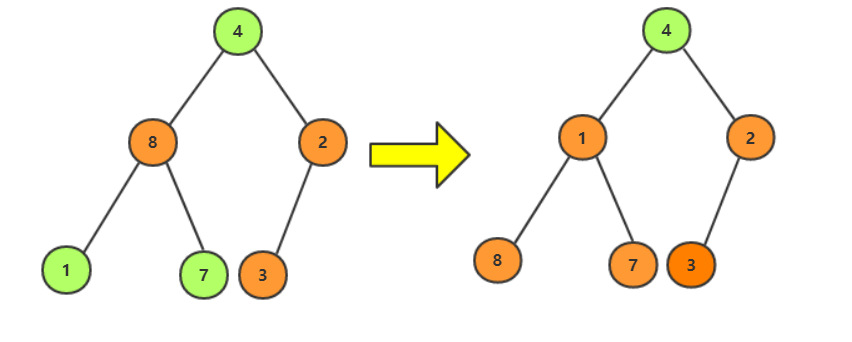
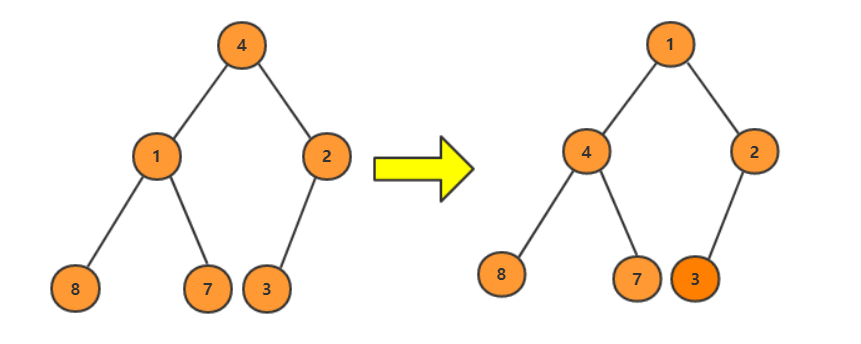
　　　　　　　　　    　此时,小堆建立完成,堆顶为数组中最小值。

　　　　　　

　　　　　　2. 向下调整　　　　　　`

　　　　　　　　　　　　　向下调整过程: 1.小堆顶部是最小值,将其与最后一个节点交换,最小值固定

　　　　　　　　　　　　　　　　　　　  2.将根节点与最小的孩子节点比较,若是不是最小值则交换,继续调整递归比较,找到合适的位置,再次形成小堆

　　　　　　　　　　　　　　　　　　　  3.循环1,2步骤直到所有值固定　　

　　　　　　1.交换1和3,固定1　

　　　　　　　

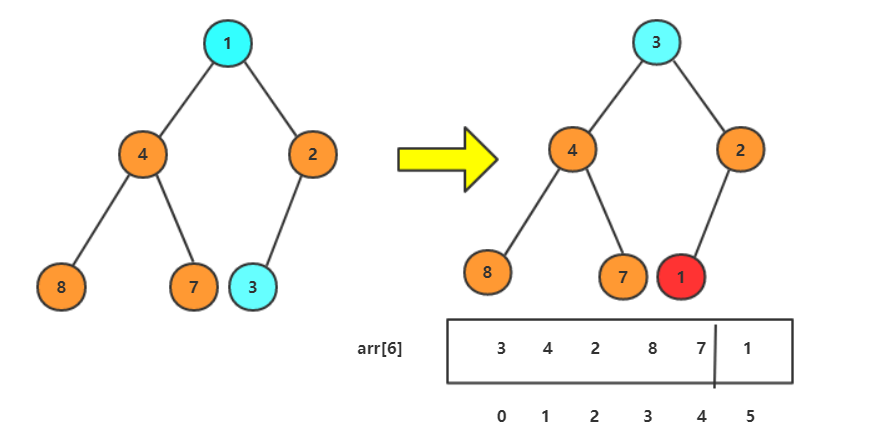
　　　　　2.向下调整形成小堆

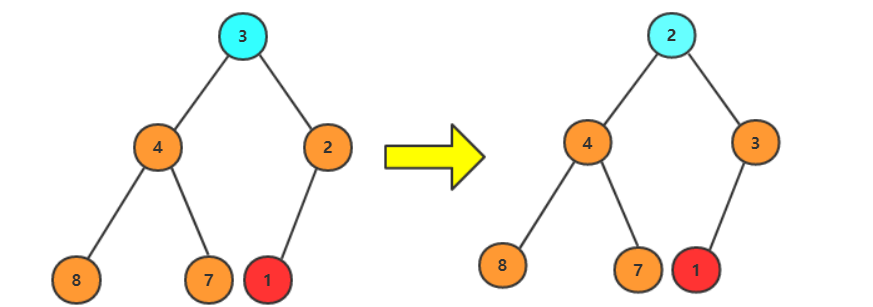
　　　　   3.重复1,2步骤直到固定所有值

　　　　　

　　　　　C/C++代码demo:

 #include<algorithm>
 //向下调整
 //和孩子比较,小了退出,大了交换
 void AdjustDown(int* arr,int n,int root)
 {
       int parent = root;
       int child = root* + ;
       //交换边界: 交换到最后的位置了
       while(child<n)
       {
           //找最小的孩子
           if(child+<n && arr[child]>arr[child+])
           {
               ++child;
           }
           //大了交换,并更新父子节点
           if(arr[parent]>arr[child])
           {
               swap(arr[parent], arr[child]);
               parent = child;
               child = *parent+;
           }
           //小了退出
           else
           {
               break;
           }
       }
 }

  //堆排序 --- 降序,造小堆
  //  下标获取方法:
 //  i->left = i*2 + 1  i->right = i*2 + 2
 //  i = (i->child-1) * 2
 void HeapSort(int* arr,int n)
 {
     //1.建堆 --- 从最后一个非叶子节点依次向下调整
     //最后一个非叶子节点确定方法: n-1的父亲,因为左对齐,所以此位置前面都有孩子
     for(int i=(n-)/;i>=;--i)
         AdjustDown(arr,n,i);

     //2.向下调整  --- 重复交换,固定,向下调整直到全部固定
     for(int end=n-;i>;--i){
         swap(arr[],arr[end])
         AdjustDown(arr,n-,i);
         }
 }