三次作业围绕表达式化简展开，逐次递进。主体思路为：递归下降解析表达式保存至类中，依据相关模式化简，依照规范输出字符串。

1.第一次作业

1.1 题目概述

表达式 = 项 + 项 + ...

项 = 因子 * 因子 * ...

因子 = {变量因子， 常数因子， 表达式因子}

变量因子 = {幂函数}

	幂函数： x ** +02、x ** 003、x ** 1

	常数因子： -003、2

	表达式因子：(x+1)**+3、(-x) 不嵌套

例：(空白字符不重要，replace预处理就好)

[input] +-+1*(-+-3*x*x**1-3*x)-x **+02*(3)**1

[output] 3*x-6*x*x

1.2 个人处理思路

初觉棘手，实验课上的代码中lexer和parser给了很好的启发，是为递归下降法。一开始怕麻烦，既然实验给的代码能解析加减、乘、括号，那便将表达式多出的乘方处理掉喂给parser即可。将过程分为预处理+解析+化简&优化+输出。

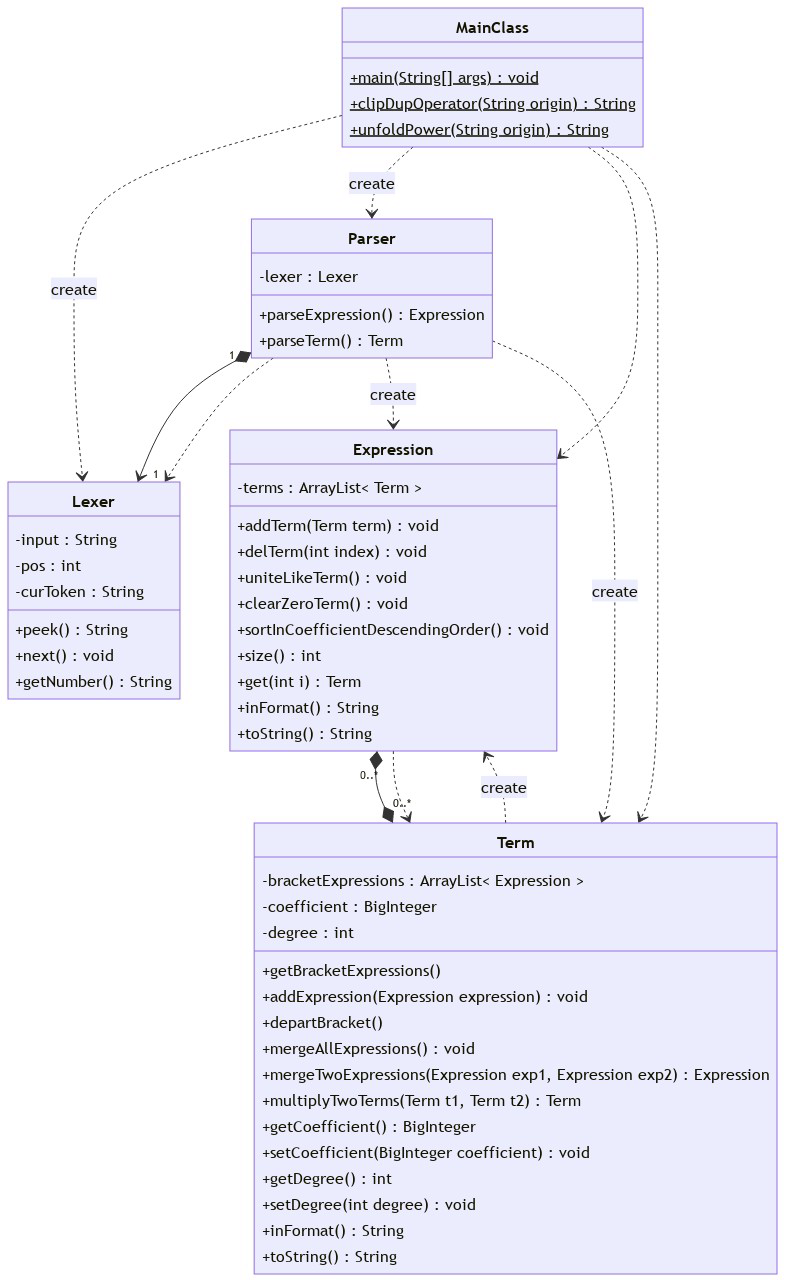
1.2.1 预处理

（1）借题目乘方指数限制，使用字符串预处理将乘方硬展成多项乘也未为不可。于是有了MainClass中预处理函数unfoldPower()，使用正则表达式匹配乘方情况（只可能是x**和(..)**），再用subString()切片拼接出新的表达式字符串。

吐槽：不可拓展的操作，纯粹钻第一次作业的空子，要改

（2）因表达式首项、项首因子、常数均可以加符号，便觉麻烦。想了想这么多符号均可以合并，那便预处理时先合并好了事。于是有了MainClass中预处理函数clipDupOperator()，使用正则表达式匹配符号（+-+3和**+02两类情形），一次只匹配两个符号，替换完后从头遍历（以防字符串变动start()移位和Matcher.find()副作用影响)。

吐槽：对符号的预处理是没有完整理解表达式结构的表现，完全没有利用好lexer和parser

1.2.2 解析

Lexer词法分析，按词义暴露读取单词(peek())；Parser获取词并解析。

parseExpression()处理表达式，遇到项parseTerm()处理项。认为化简后项自带模板a*x**b*()，便不再下分因子。项中遇表达式因子则再次parseExpression()，并将结果存入项Term类中属性ArrayList<Expression> bracketExpressions中。

1.2.3 化简&优化

由于Term类的模式集成，项中的常量和x读入时即可通过coefficient和degree化简。只剩下项中去括号和表达式中合并同类项

吐槽：degree这个词应该指整个多项式的次数而不是单项的指数，后面改回index了

（1）项中去括号：Term类中，mergeTwoExpressions()和mergeAllExpressions()将bracketExpression融合到只有1个元素；departBracket()进行乘法分配，返回项的列表，由Expression对象调用此方法并将得到的项并入自己的terms中

吐槽：违和感，Term类中处理Expression结果还要Expression中调用，应该算是内聚度不高；

mergeExpression可以在parseTerm时作为方法直接合并处理，而不是作为函数返回新Exression，这样缺少了类自身的感觉

（2）表达式合并同类项：Expression类中，uniteLikeTerm()合并同类项，clearZeroTerm()删零项，sortInCoefficientDescendingOrder()将所有项降序排列以尽可能使正向在前减少不必要的负号。

吐槽：零项直接删没了，还得在inFormat中特判处理，分工失误

1.2.4 输出

每个类配置inFormat()函数，调用Expression.inFormat()即可依次细分按规则输出。x**2换成x*x以减小长度的。

toString()是中间检验时按固有模式随便写的，没想到idea的debug会显示自动toString，属于意外之喜

1.3 度量分析

这次作业看似面向对象，但类里的方法与类关联度小，还是由面向过程的影子。(这好像并没有在度量数据里显示)

1.3.1 Class Metrics

Class OCavg OCmax WMC
Expression 2.0 6.0 20.0
Lexer 1.75 3.0 7.0
MainClass 5.666666666666667 7.0 17.0
Parser 4.0 8.0 12.0
Term 1.9333333333333333 6.0 29.0
Total 85.0
Average 2.4285714285714284 6.0 17.0

1.3.2 Method Metrics

Method CogC ev(G) iv(G) v(G)
Expression.addTerm(Term) 0.0 1.0 1.0 1.0
Expression.clearZeroTerm() 3.0 1.0 3.0 3.0
Expression.delTerm(int) 0.0 1.0 1.0 1.0
Expression.Expression() 0.0 1.0 1.0 1.0
Expression.get(int) 0.0 1.0 1.0 1.0
Expression.inFormat() 3.0 1.0 3.0 3.0
Expression.size() 0.0 1.0 1.0 1.0
Expression.sortInCoefficientDescendingOrder() 0.0 1.0 1.0 1.0
Expression.toString() 1.0 1.0 2.0 2.0
Expression.uniteLikeTerm() 11.0 5.0 4.0 6.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.next() 4.0 1.0 3.0 3.0
Lexer.peek() 0.0 1.0 1.0 1.0
MainClass.clipDupOperator(String) 9.0 1.0 5.0 6.0
MainClass.main(String[]) 7.0 3.0 4.0 5.0
MainClass.unfoldPower(String) 16.0 4.0 4.0 7.0
Parser.parseExpression() 2.0 1.0 3.0 3.0
Parser.Parser(Lexer) 0.0 1.0 1.0 1.0
Parser.parseTerm(boolean) 9.0 1.0 7.0 8.0
Term.addExpression(Expression) 0.0 1.0 1.0 1.0
Term.compareTo(Term) 3.0 3.0 2.0 3.0
Term.departBracket() 2.0 2.0 2.0 3.0
Term.getBracketExpressions() 0.0 1.0 1.0 1.0
Term.getCoefficient() 0.0 1.0 1.0 1.0
Term.getDegree() 0.0 1.0 1.0 1.0
Term.inFormat() 8.0 2.0 6.0 6.0
Term.mergeAllExpressions() 2.0 2.0 2.0 3.0
Term.mergeTwoExpressions(Expression, Expression) 3.0 1.0 3.0 3.0
Term.multiplyTwoTerms(Term, Term) 0.0 1.0 1.0 1.0
Term.setCoefficient(BigInteger) 0.0 1.0 1.0 1.0
Term.setDegree(int) 0.0 1.0 1.0 1.0
Term.Term() 0.0 1.0 1.0 1.0
Term.Term(BigInteger, int) 0.0 1.0 1.0 1.0
Term.toString() 1.0 1.0 2.0 2.0
Total 86.0 49.0 76.0 87.0
Average 2.4571428571428573 1.4 2.1714285714285713 2.4857142857142858

1.4 Bug记录与分析

本次强测100，互测未被hack

自动测评机造的数据复杂度高，具有较齐全的特征，能作为一般功能性测试。此方法hack出一个bug，属于作者独特疏漏带来的普遍bug；但无法发掘边界情况、特殊情况（极简表达式暴露、规则漏洞）

手工造的数据的数据单一，但指向性高，也考验个人对题目的细节理解。

1.4.1 个人

此次作业模式较少，未出现根本bug。仅在中测出现一疏漏bug

[1]忘修改clipDupOperator和unfoldPower预处理顺序调换带来的影响

其实换不换好像没影响，但是clip时消除了x**+2的多余符号，所以unfold的时便为考量该情况。是为修改的全面性。

1.4.2 他人

有一位是通过读代码找到的，其他2位有莫名其妙的诡异bug，懒得看了

[1] 用正则表达式消符号的疏漏

同样是预处理消多余符号

this.expression = expression.replaceAll("[ \\t]", "")  // remove blank

                     .replaceAll("-\\+|\\+-", "-")  // between terms

                     .replaceAll("--|\\+\\+", "+")  // between terms

                     .replaceAll("\\*\\+", "*");  // between factors | inside a factor

13+-+3的符号顺序即可hack出

2.第二次作业

2.1 题目概述

表达式 = 项 + 项 + ...

项 = 因子 * 因子 * ...

因子 = {变量因子， 常数因子， 表达式因子}

变量因子 = {幂函数， 三角函数， 自定义函数， 求和函数}

	幂函数： x ** +02、x ** 003、x ** 1

	三角函数： sin(x)**2、cos(x**3)

	求和函数： sum(i,3,5,因子)

	常数因子： -003、2

	表达式因子：(x+1)**+3、(-x) 不嵌套

例：(空白字符不重要，replace预处理就好)

[input]

2

f(x,y)=x+y

g(x,y)=x*sin(y)

(x+f(sin(x),x**2))*x+sum(i,3,2,sin(i))

[output]

x*x+x*sin(x)+x**3

2.2 个人处理思路

增添TriFunction、myFunction等新类应对新的因子。考虑到三角函数内同样含有多项式因子，为便于复用，将原本依附于Term类的多项式a*x**b单独开类PolyFactor。既然表达式终将互相merge为一个，不如parse到一个便merge一个，于是将原本表达式列表简化为单个表达式。新的Term模板为：

Term = PolyFactor*[sin(PolyFactor)*...]*(Expression)

意识到表达式字符串的处理，其实是预处理和解析的权衡。上一版作业解析能力差，通过预处理补齐。然而直接字符串操作的预处理显然没法面对复杂拓展情况（“复杂正则表达式会带来灾厄~”）；相反递归下降的解析手法可拓展性强，解析的复用更可以一劳永逸。这次作业便将重心移回解析，也为第三次作业打下良好基础。

同时，将上一版作业中与类关系若即若离的函数，变为了修改对象属性的方法，个人感觉内聚性强了也更有了对象的味道。将Expression和Term之间化简运算抽象为统一形式（multiplyXX()），并根据语义互相递归调用，发挥出了递归下降本该有的解析多层括号的能力。

由于函数方法的调整，这次突然意识到Java对象引用、深浅拷贝的事情，引发强烈危机感，为以防万一，手动给每个类写了deepClone()，必要时调用，并在debug时留了心眼。

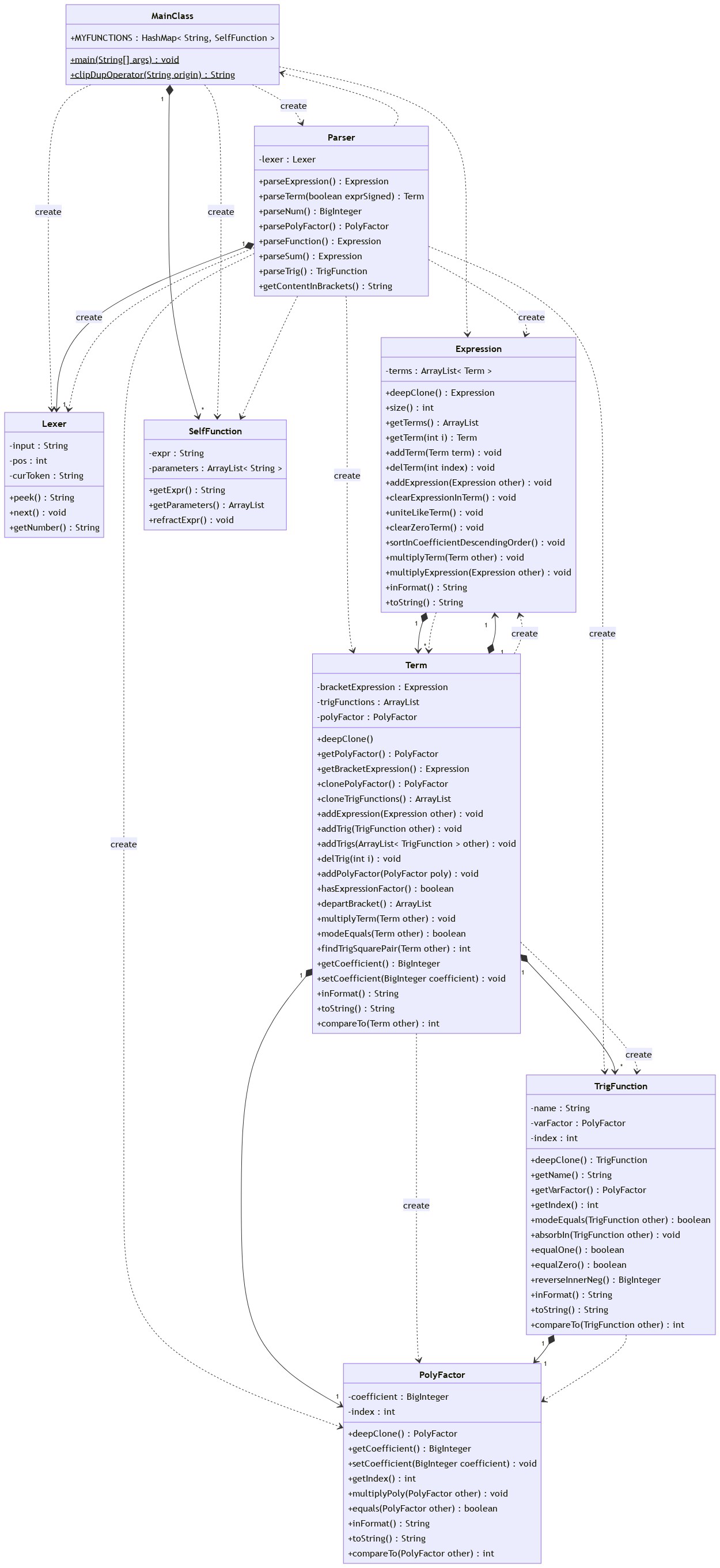
2.2.1 预处理

提前获取保存自定义函数，将其设为private以供后续解析时使用。用SelfFunction类进行记录，且配合后续解析进行了字符预处理（是个蠢蠢的字符串替换，来源于解析策略的缺点，见后）

保留了clipDupOperator()仅用于处理最后inFormat输出时多余的符号以提高性能。所以其实可以改为“后处理”

2.2.2 解析

Lexer增加了对** sin/cos sum的识别。

Parser增加了表达式、项、常量的符号处理，符合形式化定义因而可以从根本解决符号问题。增加parseNum() parsePolyFactor()方便复用，增加parseTrig() parseSum() parseFunction()以应对新因子。

其中

  • sum处理：提取出sum因子，利用字符串替换展开为不含sum的表达式，喂给新的parser.parseExpression()返回Expression给Term；

吐槽：由于sum中循环变量i和求和表达式中sin()的i重复，若使用replace()会误替换，因而事先将sin换成其他字符(如#)，replace完后再换回

String sumTerm = getContentInBrackets().replaceAll("sin", "#");

StringBuilder sb = new StringBuilder();

while (start.compareTo(end) <= 0) {

    sb.append("+").append(sumTerm.replaceAll("i", start.toString()));

    start = start.add(BigInteger.ONE);

}

if (sb.length() == 0) {

    sb.append("0");

}

String expr = sb.toString().replaceAll("#", "sin");

这种“技巧”在本次作业多次使用，是为字符串处理的劣势，拓展性差

  • function处理：提取function因子，利用split(",")提取参数（记为argument）；再和记录的函数变量（记为parameter）配对成Hashmap；遍历键值对，进行字符串替换（先替换变量x，以防后续argument和parameter中x混淆导致的替换错误），喂给新的parser.parseExpression()返回Expression给Term

吐槽：String.split()方法再次展现了字符串处理的糟糕拓展性，这将成为第三次作业的bug

将parmeters替换为arguments会引入不合法的表达式:

Funciton Parameter = Argument Result Wish
x**2 x = 2 2**2 不合法！ 带入时给Argument带括号，(2)**2即合法
sin(x**2) x = x sin(x**2) 合法 不希望带括号，若带括号sin((x)**2)即不合法

两者不能兼顾，便考虑对表达式预处理，代入时不加括号；然而仍需要分类讨论，对于单独x**2，进行展开x*x；对于在三角函数内部sin(x**2)不进行展开。这般用正则表达式势必会有模式误判，便采用了类似sum函数i替换的技巧：先依次将sin(...)记录并替换为无关字符，再匹配[xyz]**进行展开，最后再依次将无关字符替换会sin(...)

吐槽：总之就是非常流氓，当然也有一部分原因是parser功能不完善

2.2.3 化简&优化

将所有化简&优化方法集成到了每一个类中。同时也引发了一些对于对象引用/深浅拷贝理解不足带来的bug（详细见下）。

clearZeroTerm()时若只剩下一项且为0，则不删除；这样就不需再inFormat()中特判。

新实现优化：

  • 基于sin(x)**2 + cos(x)**2 = 1的正向化简（包括部分提取公因式后类似结果）
  • 基于sin(-x) = - sin(x), cos(-x) = cos(x)的符号外提

2.2.4 输出

稍微在inFormat中传入一些参数，以控制x**2是否以x*x输出

为了Term及以下的类实现Comparable接口排序便于优化

2.3 度量分析

2.3.1 Class Metrics

Class OCavg OCmax WMC
Expression 2.176470588235294 8.0 37.0
Lexer 2.5 6.0 10.0
MainClass 4.0 5.0 8.0
Parser 4.0 12.0 36.0
PolyFactor 2.0 7.0 20.0
SelfFunction 3.0 9.0 12.0
Term 2.347826086956522 9.0 54.0
TrigFunction 1.7692307692307692 7.0 23.0
Total 200.0
Average 2.4390243902439024 7.875 25.0

2.3.2 Method Metrics

Method CogC ev(G) iv(G) v(G)
Expression.addExpression(Expression) 0.0 1.0 1.0 1.0
Expression.addTerm(Term) 0.0 1.0 1.0 1.0
Expression.clearExpressionInTerm() 5.0 3.0 3.0 4.0
Expression.clearZeroTerm() 6.0 1.0 4.0 4.0
Expression.deepClone() 1.0 1.0 2.0 2.0
Expression.delTerm(int) 0.0 1.0 1.0 1.0
Expression.Expression() 0.0 1.0 1.0 1.0
Expression.Expression(ArrayList) 0.0 1.0 1.0 1.0
Expression.getTerm(int) 0.0 1.0 1.0 1.0
Expression.getTerms() 0.0 1.0 1.0 1.0
Expression.inFormat() 3.0 1.0 3.0 3.0
Expression.multiplyExpression(Expression) 4.0 1.0 3.0 3.0
Expression.multiplyTerm(Term) 1.0 1.0 2.0 2.0
Expression.size() 0.0 1.0 1.0 1.0
Expression.sortInCoefficientDescendingOrder() 0.0 1.0 1.0 1.0
Expression.toString() 1.0 1.0 2.0 2.0
Expression.uniteLikeTerm() 22.0 5.0 6.0 8.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.next() 12.0 5.0 8.0 8.0
Lexer.peek() 0.0 1.0 1.0 1.0
MainClass.clipDupOperator(String) 9.0 1.0 5.0 6.0
MainClass.main(String[]) 3.0 1.0 3.0 3.0
Parser.getContentInBrackets() 9.0 4.0 2.0 5.0
Parser.parseExpression() 2.0 1.0 3.0 3.0
Parser.parseFunction() 4.0 1.0 5.0 5.0
Parser.parseNum() 1.0 1.0 2.0 2.0
Parser.parsePolyFactor() 4.0 1.0 3.0 3.0
Parser.Parser(Lexer) 0.0 1.0 1.0 1.0
Parser.parseSum() 2.0 1.0 3.0 3.0
Parser.parseTerm(boolean) 17.0 1.0 11.0 12.0
Parser.parseTrig() 1.0 1.0 2.0 2.0
PolyFactor.compareTo(PolyFactor) 4.0 5.0 3.0 5.0
PolyFactor.deepClone() 0.0 1.0 1.0 1.0
PolyFactor.equals(PolyFactor) 1.0 1.0 2.0 2.0
PolyFactor.getCoefficient() 0.0 1.0 1.0 1.0
PolyFactor.getIndex() 0.0 1.0 1.0 1.0
PolyFactor.inFormat(boolean) 10.0 3.0 7.0 8.0
PolyFactor.multiplyPoly(PolyFactor) 0.0 1.0 1.0 1.0
PolyFactor.PolyFactor(BigInteger, int) 0.0 1.0 1.0 1.0
PolyFactor.setCoefficient(BigInteger) 0.0 1.0 1.0 1.0
PolyFactor.toString() 0.0 1.0 1.0 1.0
SelfFunction.getExpr() 0.0 1.0 1.0 1.0
SelfFunction.getParameters() 0.0 1.0 1.0 1.0
SelfFunction.refractExpr() 14.0 5.0 5.0 9.0
SelfFunction.SelfFunction(String, String[]) 0.0 1.0 1.0 1.0
Term.addExpression(Expression) 1.0 2.0 2.0 2.0
Term.addPolyFactor(PolyFactor) 0.0 1.0 1.0 1.0
Term.addTrig(TrigFunction) 6.0 5.0 5.0 6.0
Term.addTrigs(ArrayList) 1.0 1.0 2.0 2.0
Term.clonePolyFactor() 0.0 1.0 1.0 1.0
Term.cloneTrigFunctions() 1.0 1.0 2.0 2.0
Term.compareTo(Term) 3.0 3.0 2.0 3.0
Term.deepClone() 2.0 1.0 3.0 3.0
Term.delTrig(int) 0.0 1.0 1.0 1.0
Term.departBracket() 2.0 2.0 2.0 3.0
Term.findTrigSquarePair(Term) 16.0 9.0 6.0 9.0
Term.getBracketExpression() 0.0 1.0 1.0 1.0
Term.getCoefficient() 0.0 1.0 1.0 1.0
Term.getPolyFactor() 0.0 1.0 1.0 1.0
Term.hasExpressionFactor() 0.0 1.0 1.0 1.0
Term.inFormat() 7.0 4.0 7.0 7.0
Term.modeEquals(Term) 9.0 5.0 3.0 5.0
Term.multiplyTerm(Term) 0.0 1.0 1.0 1.0
Term.setCoefficient(BigInteger) 0.0 1.0 1.0 1.0
Term.Term(BigInteger, int) 0.0 1.0 1.0 1.0
Term.Term(PolyFactor, ArrayList) 0.0 1.0 1.0 1.0
Term.Term(PolyFactor, ArrayList, Expression) 0.0 1.0 1.0 1.0
Term.toString() 1.0 1.0 2.0 2.0
TrigFunction.absorbIn(TrigFunction) 0.0 1.0 1.0 1.0
TrigFunction.compareTo(TrigFunction) 7.0 6.0 4.0 7.0
TrigFunction.deepClone() 0.0 1.0 1.0 1.0
TrigFunction.equalOne() 2.0 1.0 3.0 3.0
TrigFunction.equalZero() 1.0 1.0 2.0 2.0
TrigFunction.getIndex() 0.0 1.0 1.0 1.0
TrigFunction.getName() 0.0 1.0 1.0 1.0
TrigFunction.getVarFactor() 0.0 1.0 1.0 1.0
TrigFunction.inFormat() 1.0 1.0 1.0 2.0
TrigFunction.modeEquals(TrigFunction) 1.0 1.0 2.0 2.0
TrigFunction.reverseInnerNeg() 7.0 3.0 3.0 4.0
TrigFunction.toString() 0.0 1.0 1.0 1.0
TrigFunction.TrigFunction(String, PolyFactor, int) 0.0 1.0 1.0 1.0
Total 206.0 135.0 184.0 212.0
Average 2.512 1.646 2.244 2.585

2.4 Bug记录与分析

本次强测86.67，错两个点，两个bug；互测因彼两bug被hack较惨

复杂度上升了，bug也出现了。主要产出于优化部分（没有优化就没有伤害）

2.4.1 个人

[1] Lexer移位过头/不及

lexer类似迭代器，本次在各类parse函数中大量手动使用lexer.next()，易产生解析完后 多/少next() 导致提前退出解析。例如：sum(i,2,3,i)*3解析sum后lexer.peek()停留在)提前退出parseTerm()

多函数配合时这种疏漏更易发生，且一个函数更改后，要记得同时调整另一个函数。

最好的办法就是提前立规矩：每一个parse结束后，lexer必须停留在为解析字符上。是为标准化，方便各函数对接，调试也容易定位。

[2] sin(x)**2 + cos(x)**2 优化后不管系数直接改1了

这种属于个人特殊性疏漏，难以通过统一方法论避免。只能说写代码时聚精会神，并提前立flag调试时重点关注

[3] 未考虑sum(i,s,e,...)中s>e的情况

审题向来重中之重，尤其长题。写完后应重新读题以防疏漏功能，切忌自以为是。第三次作业一bug也源于此

[4] 手抖将this写成other，导致比较错误

此类手抖层出不穷。尤其时重复/模式相近的代码，易手滑。上学期计组p5也有这类bug

[5] sin(-x)**n化简时未考虑指数影响 （强测&互测）

n为偶数时，负号应直接扔去。

这种疏忽。。只能说多测吧

[6] sin(x)**2 + cos(x)**2 优化 奇怪的操作 （强测&互测）



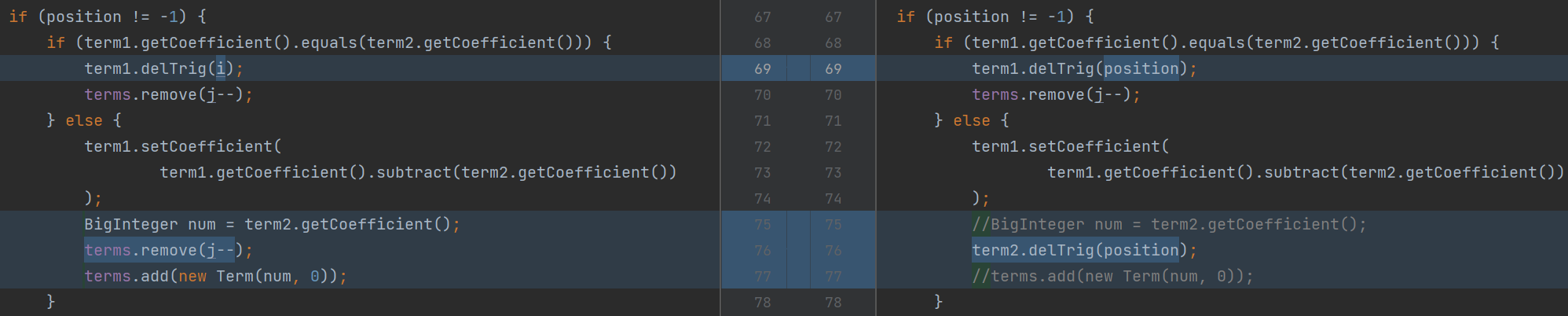
和2其实挺类似，都是莫名其妙的疏漏，事后是毫无知觉的

2.4.2 他人

这次只有hack出一个0未输出的错误，其他也hack不出啥

3.第三次作业

3.1 题目概述

新增：

函数可以嵌套调用；三角函数内可以嵌套因子

没多管，只要处理好各因子套表达式的模型，就能一劳永逸

3.2 个人处理思路

经历第二次作业半重构后，这次作业跨度意外的小。

将sin()中的PolyFactor换成Expression，便可毫无顾虑的处理三角函数内合法表达式，覆盖了题目限制的嵌套因子。新Term模板为：

Term = PolyFactor*[sin(Expression)*...]*(Expression)

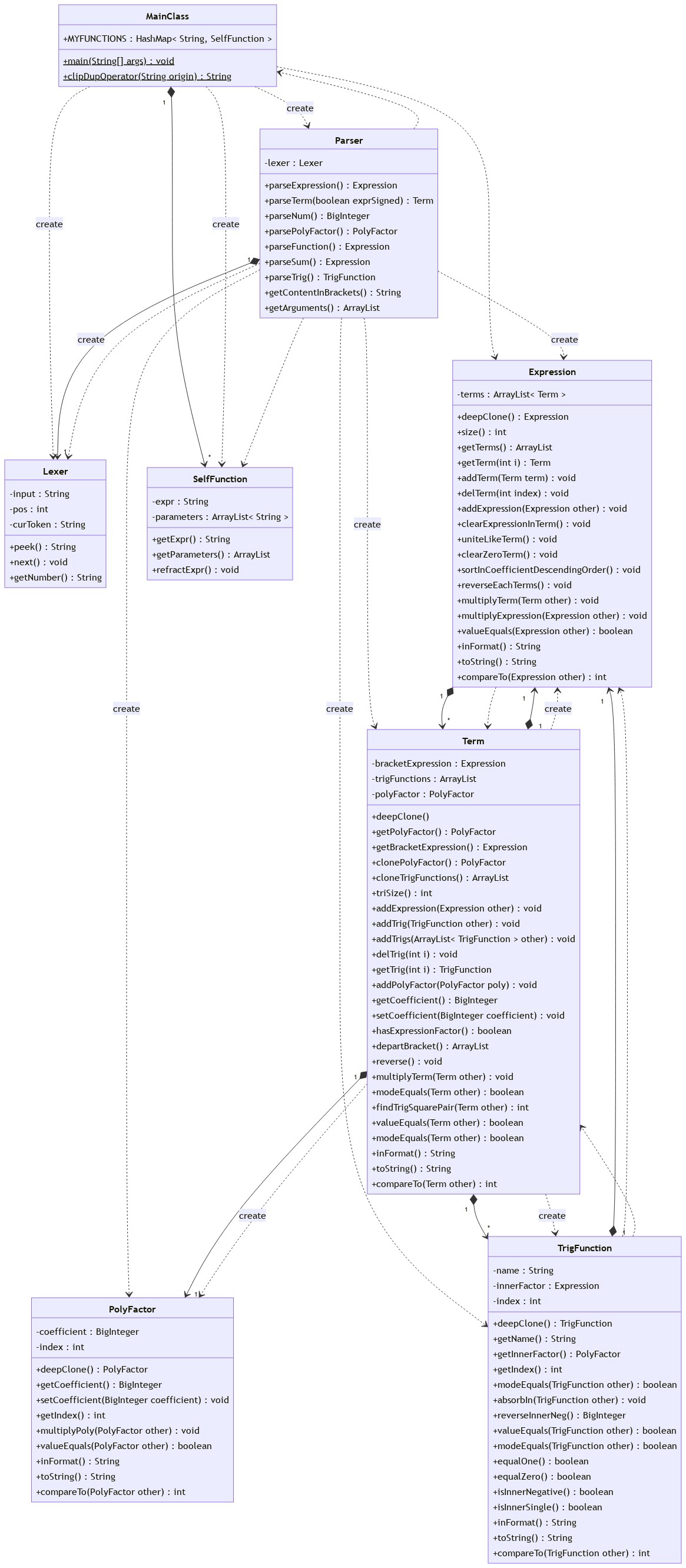
考虑了一下equals的含义，为所需存储类专门写valueEquals()和modeEquals()以防搞错；

为每一个存储类实现了Comparable接口，递归调用两类Equals分出了所有存储类的大小，便于排序后进行模式匹配从而是实现优化

吐槽：到目前位置，这几个存储类都有了好一部分相同的函数，呈现出一部分共同模式，似乎有接口/抽象类可以抽取。但具体用处还得考量。

function调用处理时，因嵌套（类似f(sum(i,1,2,sin(i)),x**2)）无法使用split(",")来获取参数，便新写getArgument()。对function调用内部依次进行parseExpression()传回字符串作为argument

吐槽：好像略微明白助教老师强调的“对函数进行解析而不是字符串替换”，但由于自己的Parser不支持多变量，所以只改了一半。

3.3 度量分析

论理圈复杂度等高的地方，容易出bug。但我觉的这是只是一种难点易错点的反馈，毕竟复杂的属性就在那里。（但确实要尽可能通过简化复杂度来降低出bug的风险）

3.3.1 Class Metrics

Class OCavg OCmax WMC
Expression 2.55 8.0 51.0
Lexer 2.5 6.0 10.0
MainClass 4.0 5.0 8.0
Parser 3.8 12.0 38.0
PolyFactor 2.0 7.0 20.0
SelfFunction 2.25 6.0 9.0
Term 2.5714285714285716 11.0 72.0
TrigFunction 1.9375 7.0 31.0
Total 239.0
Average 2.5425531914893615 7.75 29.875

复杂度是愈来愈高了，迭代开发的通病（？），毕竟只添内容方便，结构性颠覆总是胆战心惊。

3.3.2 Method Metrics

Method CogC ev(G) iv(G) v(G)
Expression.addExpression(Expression) 0.0 1.0 1.0 1.0
Expression.addTerm(Term) 0.0 1.0 1.0 1.0
Expression.clearExpressionInTerm() 5.0 3.0 3.0 4.0
Expression.clearZeroTerm() 6.0 1.0 4.0 4.0
Expression.compareTo(Expression) 7.0 7.0 4.0 7.0
Expression.deepClone() 1.0 1.0 2.0 2.0
Expression.delTerm(int) 0.0 1.0 1.0 1.0
Expression.Expression() 0.0 1.0 1.0 1.0
Expression.Expression(ArrayList) 0.0 1.0 1.0 1.0
Expression.getTerm(int) 0.0 1.0 1.0 1.0
Expression.getTerms() 0.0 1.0 1.0 1.0
Expression.inFormat(boolean, boolean) 5.0 2.0 4.0 4.0
Expression.multiplyExpression(Expression) 4.0 1.0 3.0 3.0
Expression.multiplyTerm(Term) 1.0 1.0 2.0 2.0
Expression.reverseEachTerms() 1.0 1.0 2.0 2.0
Expression.size() 0.0 1.0 1.0 1.0
Expression.sortInCoefficientDescendingOrder() 0.0 1.0 1.0 1.0
Expression.toString() 1.0 1.0 2.0 2.0
Expression.uniteLikeTerm() 22.0 5.0 6.0 8.0
Expression.valueEquals(Expression) 4.0 4.0 2.0 4.0
Lexer.getNumber() 2.0 1.0 3.0 3.0
Lexer.Lexer(String) 0.0 1.0 1.0 1.0
Lexer.next() 12.0 5.0 8.0 8.0
Lexer.peek() 0.0 1.0 1.0 1.0
MainClass.clipDupOperator(String) 9.0 1.0 5.0 6.0
MainClass.main(String[]) 3.0 1.0 3.0 3.0
Parser.getArguments() 1.0 1.0 2.0 2.0
Parser.getContentInBrackets() 9.0 4.0 2.0 5.0
Parser.parseExpression() 2.0 1.0 3.0 3.0
Parser.parseFunction() 4.0 1.0 5.0 5.0
Parser.parseNum() 1.0 1.0 2.0 2.0
Parser.parsePolyFactor() 4.0 1.0 3.0 3.0
Parser.Parser(Lexer) 0.0 1.0 1.0 1.0
Parser.parseSum() 2.0 1.0 3.0 3.0
Parser.parseTerm(boolean) 17.0 1.0 11.0 12.0
Parser.parseTrig() 1.0 1.0 2.0 2.0
PolyFactor.compareTo(PolyFactor) 4.0 5.0 3.0 5.0
PolyFactor.deepClone() 0.0 1.0 1.0 1.0
PolyFactor.getCoefficient() 0.0 1.0 1.0 1.0
PolyFactor.getIndex() 0.0 1.0 1.0 1.0
PolyFactor.inFormat(boolean) 10.0 3.0 7.0 8.0
PolyFactor.multiplyPoly(PolyFactor) 0.0 1.0 1.0 1.0
PolyFactor.PolyFactor(BigInteger, int) 0.0 1.0 1.0 1.0
PolyFactor.setCoefficient(BigInteger) 0.0 1.0 1.0 1.0
PolyFactor.toString() 0.0 1.0 1.0 1.0
PolyFactor.valueEquals(PolyFactor) 1.0 1.0 2.0 2.0
SelfFunction.getExpr() 0.0 1.0 1.0 1.0
SelfFunction.getParameters() 0.0 1.0 1.0 1.0
SelfFunction.refractExpr() 10.0 3.0 3.0 6.0
SelfFunction.SelfFunction(String, String[]) 0.0 1.0 1.0 1.0
Term.addExpression(Expression) 1.0 2.0 2.0 2.0
Term.addPolyFactor(PolyFactor) 0.0 1.0 1.0 1.0
Term.addTrig(TrigFunction) 6.0 5.0 5.0 6.0
Term.addTrigs(ArrayList) 1.0 1.0 2.0 2.0
Term.clonePolyFactor() 0.0 1.0 1.0 1.0
Term.cloneTrigFunctions() 1.0 1.0 2.0 2.0
Term.compareTo(Term) 11.0 11.0 6.0 11.0
Term.deepClone() 2.0 1.0 3.0 3.0
Term.delTrig(int) 0.0 1.0 1.0 1.0
Term.departBracket() 2.0 2.0 2.0 3.0
Term.findTrigSquarePair(Term) 16.0 9.0 6.0 9.0
Term.getBracketExpression() 0.0 1.0 1.0 1.0
Term.getCoefficient() 0.0 1.0 1.0 1.0
Term.getIndex() 0.0 1.0 1.0 1.0
Term.getPolyFactor() 0.0 1.0 1.0 1.0
Term.getTrig(int) 0.0 1.0 1.0 1.0
Term.hasExpressionFactor() 0.0 1.0 1.0 1.0
Term.inFormat(boolean) 7.0 4.0 7.0 7.0
Term.modeEquals(Term) 5.0 5.0 2.0 5.0
Term.multiplyTerm(Term) 0.0 1.0 1.0 1.0
Term.reverse() 0.0 1.0 1.0 1.0
Term.setCoefficient(BigInteger) 0.0 1.0 1.0 1.0
Term.Term(BigInteger, int) 0.0 1.0 1.0 1.0
Term.Term(PolyFactor, ArrayList) 0.0 1.0 1.0 1.0
Term.Term(PolyFactor, ArrayList, Expression) 0.0 1.0 1.0 1.0
Term.toString() 1.0 1.0 2.0 2.0
Term.triSize() 0.0 1.0 1.0 1.0
Term.valueEquals(Term) 6.0 6.0 2.0 6.0
TrigFunction.absorbIn(TrigFunction) 0.0 1.0 1.0 1.0
TrigFunction.compareTo(TrigFunction) 7.0 6.0 4.0 7.0
TrigFunction.deepClone() 0.0 1.0 1.0 1.0
TrigFunction.equalOne() 3.0 3.0 2.0 4.0
TrigFunction.equalZero() 2.0 2.0 2.0 3.0
TrigFunction.getIndex() 0.0 1.0 1.0 1.0
TrigFunction.getInnerFactor() 0.0 1.0 1.0 1.0
TrigFunction.getName() 0.0 1.0 1.0 1.0
TrigFunction.inFormat() 1.0 1.0 1.0 2.0
TrigFunction.isInnerNegative() 0.0 1.0 1.0 1.0
TrigFunction.isInnerSingle() 7.0 4.0 4.0 5.0
TrigFunction.modeEquals(TrigFunction) 1.0 1.0 2.0 2.0
TrigFunction.reverseInnerNeg() 4.0 2.0 3.0 4.0
TrigFunction.toString() 0.0 1.0 1.0 1.0
TrigFunction.TrigFunction(String, Expression, int) 0.0 1.0 1.0 1.0
TrigFunction.valueEquals(TrigFunction) 1.0 1.0 3.0 3.0
Total 234.0 173.0 209.0 254.0
Average 2.4893617021276597 1.8404255319148937 2.223404255319149 2.702127659574468

3.4 Bug记录与分析

此次强测96.89，性能上确实有自知的不足（懒待改进了），互测发现两个bug，被hack惨了

3.4.1 个人

[1] 新加的getArgument()又没处理好lexer.next()问题

和上一次作业一样了，插眼

[2] 优化失效：每次addTrig后，三角函数列表可能会无序，导致之后的优化失效

每次加完三角函数，都重新排一遍序

[3] 合并同类项的二重for循环中，内层循环有权限改变外层循环变量i，但相应的引用对象没变，导致内容错位 （互测）

这就是代码编写习惯不好了，内层循环尽量不要修改外循环的东西，有也要考虑到修改完后，自己仍处于内层循环！

[4] 未考虑sum(i,..,..,i**2)的情况 （互测）

这就是前面提到的审题疏忽。哪怕我写完后重看一遍题目，便会在形式化表达那栏发现

幂函数 → (函数自变量|'i') [空白项 指数]

3.4.2 他人

找不到。我提供了房间所有的bug

4.总结与心得

构架上，第一次到第二次的修改跨度较大，但也算是走上正轨；第二次到第三次便自然而然的轻松了许多。

此单元作业的收获有下：

  • 认识了递归下降这种语言分析方式
  • 对Java的对象引用、深浅拷贝有了深刻印象
  • 构造随机数据和测评机时，学到了一些python库和调用其他程序的方法
  • 体验了重构（半重构）、迭代开发的具体实感，有了些许经验之谈
  • 可能有了些许面向对象程序的感觉（？）

还有，OO让我充实，自发的减少了摸鱼的时间，感谢。以及这周没OO又摸起来了，呜呜

【Unit1】表达式化简（层次化设计）-作业总结的更多相关文章

  1. 求和：fft，表达式化简

    $f(n)=\sum\limits_{i=0}^{n} \sum\limits_{j=0}^{i} S(i,j) \times 2^j \times j!$ 其中$S(i,j)$为第二类斯特林数,公式 ...

  2. B/b.cpp:表达式化简，二分答案

    不知道能不能粘题面于是不粘了. 首先声明这道题可以怎么水过: 随机化几万次操作,取最优答案. 暴力O(n2log n)可过. 不想打正解的可以走了. emm然而我的应该是正解,O(n log n). ...

  3. Quine-McCluskey两级逻辑化简算法原理解析

    转载请务必注明出处:https://www.cnblogs.com/the-wind/p/15764283.html 目录 1 背景介绍:两级逻辑 2 Quine-McCluskey两级逻辑化简 2. ...

  4. 【mongoDB高级篇②】大数据聚集运算之mapReduce(映射化简)

    简述 mapReduce从字面上来理解就是两个过程:map映射以及reduce化简.是一种比较先进的大数据处理方法,其难度不高,从性能上来说属于比较暴力的(通过N台服务器同时来计算),但相较于grou ...

  5. atitit.  web组件化原理与设计

    atitit.  web组件化原理与设计 1. Web Components提供了一种组件化的推荐方式,具体来说,就是:1 2. 组件化的本质目的并不一定是要为了可复用,而是提升可维护性. 不具有复用 ...

  6. matlab化简符号表达式

    化简符号表达式计算机毕竟还是挺笨的, 经过一系列的符号计算后, 得到的结果可能只有它自己才能看懂, Matlab提供大量函数以用于符号表达式的化简. collect(f): 函数用途是合并多项式中相同 ...

  7. AppBox升级进行时 - 扁平化的权限设计

    AppBox 是基于 FineUI 的通用权限管理框架,包括用户管理.职称管理.部门管理.角色管理.角色权限管理等模块. AppBox v2.0中的权限实现 AppBox v2.0中权限管理中涉及三个 ...

  8. NOIP201402比例化简

    比例化简 [问题描述]在社交媒体上,经常会看到针对某一个观点同意与否的民意调查以及结果.例如,对某一观点表示支持的有 1498 人,反对的有 902 人,那么赞同与反对的比例可以简单的记为1498:9 ...

  9. YZOI Easy Round 2_化简（simplify.c/cpp/pas)

    Description 给定一个多项式,输出其化简后的结果. Input 一个字符串,只含有关于字母x 的多项式,不含括号与分式,没有多余的空格. Output 一个字符串,化简后的多项式,按照次数从 ...

  10. 化简复杂逻辑，编写紧凑的if条件语句

    当业务逻辑很复杂,涉及多个条件的真假,或者多种条件下都会执行同一动作时,如何编写紧凑的if语句呢?本文借由一个实际例子,利用数学的布尔逻辑整理条件,最终产生if语句. 问题 在<X3 重聚> ...

随机推荐

  1. java到报名的编码运行

    Hello.java package a.b; import com.beyondiary.kit.KitConstant; public class Hello { public static vo ...

  2. MyBatisPlus中updateById与updateAllColumnById方法区别

    实现 updateById方法在插入时,会根据实体类的每个属性进行非空判断,只有非空的属性所对应的字段才会出现在SQL语句中. updateAllColumnById方法在插入时,不管属性是否为空,属 ...

  3. Qt/C++自定义界面大全/20套精美皮肤/26套精美UI界面/一键换肤/自定义颜色/各种导航界面

    一.前言 这个系列对应自定义控件大全,一个专注于控件的编写,一个专注于UI界面的编写,程序员有两大软肋,一个是忌讳别人说自己的程序很烂很多bug,一个就是不擅长UI,基本上配色就直接rgb,对于第一点 ...

  4. Qt编写安防视频监控系统36-onvif连续移动

    一.前言 时隔一年多,重新对视频监控系统的onvif内核重写,一方面为了兼容Qt6,一方面按功能分类提高效率.整体逻辑思路是一样的,主要的改动是由于Qt6不再支持QtXmlPatterns模块(其实这 ...

  5. IM开发者的零基础通信技术入门(十三)：为什么手机信号差？一文即懂！

    [来源申明]本文引用了微信公众号"网优雇佣军"的<是谁偷走了我家的手机信号?>文章内容.为了更好的内容呈现,下文在引用和收录时内容有改动,转载时请注明原文来源信息,尊重 ...

  6. 揭秘百度IM消息中台的全量用户消息推送技术改造实践

    本文内容由百度技术团队分享,原题"基于公共信箱的全量消息实现",为了帮助理解,有较多修订.内容重组和重新排版. 1.引言 百度的IM消息中台为百度APP以及厂内百度系产品提供即时通 ...

  7. PaperAssistant：使用Microsoft.Extensions.AI实现

    前言 上篇文章介绍了使用Semantic Kernel Chat Completion Agent实现的版本. 使用C#构建一个论文总结AI Agent 今天来介绍一下使用Microsoft.Exte ...

  8. 《刚刚问世》系列初窥篇-Java+Playwright自动化测试-10- 标签页（tab）操作 - 上篇 （详细教程）

    1.简介 本来按照计划这一系列的文章应该介绍Context和Page两个内容的,但是宏哥看了官方文档和查找资料发现其实和宏哥在Python+Playwright系列文章中的大同小异,差不了多少,再在这 ...

  9. Java常用的并发类-总结列表

    一.java集合框架概述 java集合可分为Collection和Map两种体系,其中: 1.Collection接口:单列数据,定义了存取一组对象的方法的集合: List:元素有序.可重复的集合 S ...

  10. RPC框架的实现原理，及RPC架构组件详解

    RPC的由来 随着互联网的发展,网站应用的规模不断扩大,常规的垂直应用架构已无法应对,分布式服务架构以及流动计算架构势在必行,亟需一个治理系统确保架构有条不紊的演进. 单一应用架构 当网站流量很小时, ...