[UR #3] 核聚变反应强度

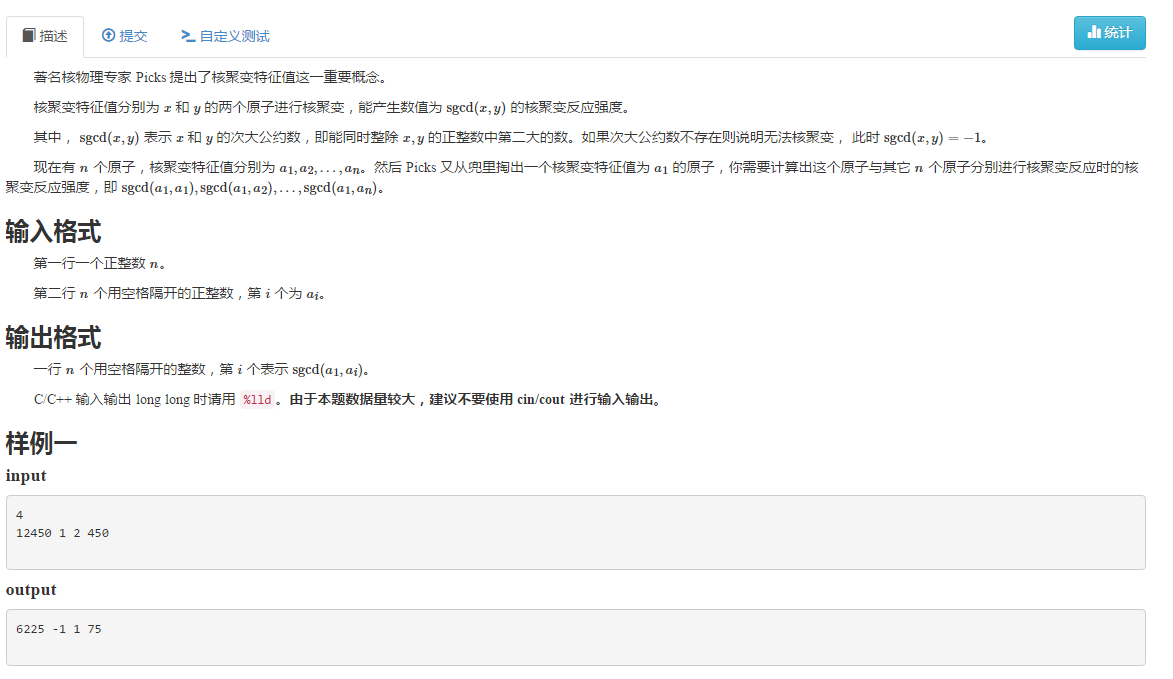
次大公约数就是gcd再除以其最小质因子(如果有的话)。可以发现要求的sgcd 的前身gcd都是a1的约数，所以把a1质因数分解直接做就行了。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=100005;
unordered_map<ll,ll> mmp;
ll gcd(ll x,ll y){ return y?gcd(y,x%y):x;}
int n,c[233],num;
ll a,d[233],now;

void dfs(int x,ll y,ll Min){
	if(x==num){ mmp[y]=Min?y/Min:-1; return;}
	dfs(x+1,y,Min),y*=d[x+1];
	if(!Min) Min=d[x+1];
	for(int u=1;u<=c[x+1];u++,y*=(ll)d[x+1]) dfs(x+1,y,Min);
}

inline void prework(ll x){
	for(int i=2;i*(ll)i<=x;i++) if(!(x%i)){
		d[++num]=i;
		for(;!(x%i);c[num]++,x/=i);
	}
	if(x!=1) d[++num]=x,c[num]=1;

	dfs(0,1,0);
}

inline void output(){
	printf("%lld ",mmp[a]);
	for(int i=2;i<=n;i++) scanf("%lld",&now),printf("%lld ",mmp[gcd(a,now)]);
}

int main(){
	scanf("%d%lld",&n,&a);
	prework(a);
	output();
	return 0;
}