JZOJ 4299. 【NOIP2015模拟11.2晚】舳舻牌

题目

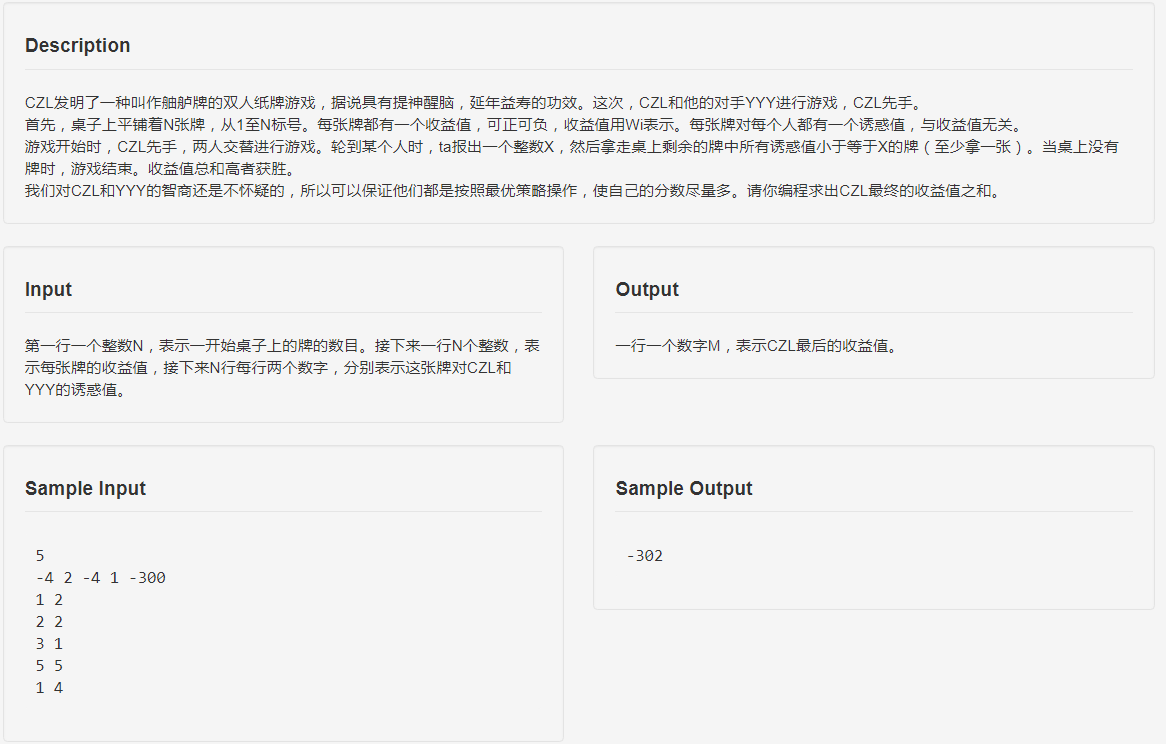
思路

倒序 \(DP\)

设 \(f_{i,j}\) 表示 \(A\) 先手，当前 \(A\) 报出的值为 \(i\)，\(B\) 报出的值为 \(j\)，\(A\) 取诱惑值大于等于 \(i\) 的， \(A\) 能拿到的最大收益

\(g_{i,j}\) 表示 \(B\) 先手，当前 \(B\) 报出的值为 \(j\)，\(A\) 报出的值为 \(i\)，\(B\) 取诱惑值大于等于 \(j\) 的，\(B\) 能拿到的最大收益（和 \(f\) 同理）

那么我们考虑转移 \(f_{i,j}=\max(sum_{i,j} - g_{k,j}) i + 1 \leq k \leq n\)

\(sum_{i,j}\) 和 \(f,g\) 的意思差不多，就是改成全取的总收益

\(g\) 转移同理

但其中有个很重要的细节：每次转移必须选数

所以我们要记录 \(cnt_{i,j}\) 表示和 \(sum\) 差不多，但它存的是诱惑值范围内数的个数

当本次转移的 \(cnt_{i,j}\) 等于上次转移用的 \(cnt\) 时，直接继承

一看，what out?! \(O(n^3)\) 的！！

不可接受

但我们发现转移时总有一维是固定

我们可以开个数组算完 \(f\) 后更新最优值

这样就可以做到 \(O(1)\) 转移

注意先离散化，求 \(sum，cnt\) 时用二维前缀和

\(Code\)

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;

const int N = 1005;
int n;
LL f[N][N] , g[N][N] , a[N] , b[N] , c[N] , val[N] , sum[N][N] , cnt[N][N];

int main()
{
	freopen("poker.in" , "r" , stdin);
	freopen("poker.out" , "w" , stdout);

	scanf("%d" , &n);
	for(register int i = 1; i <= n; i++) scanf("%lld" , &val[i]);
	for(register int i = 1; i <= n; i++) scanf("%lld%lld" , &a[i] , &b[i]);

	for(register int i = 1; i <= n; i++) c[i] = a[i];
	sort(c + 1 , c + n + 1);
	int m = unique(c + 1 , c + n + 1) - c - 1;
	for(register int i = 1; i <= n; i++) a[i] = lower_bound(c + 1 , c + m + 1 , a[i]) - c;

	for(register int i = 1; i <= n; i++) c[i] = b[i];
	sort(c + 1 , c + n + 1);
	m = unique(c + 1 , c + n + 1) - c - 1;
	for(register int i = 1; i <= n; i++) b[i] = lower_bound(c + 1 , c + m + 1 , b[i]) - c;

	for(register int i = 1; i <= n; i++)
		++cnt[a[i]][b[i]] , sum[a[i]][b[i]] += val[i];
	for(register int i = n; i; i--)
		for(register int j = n; j; j--)
		{
			sum[i][j] += sum[i + 1][j] + sum[i][j + 1] - sum[i + 1][j + 1];
			cnt[i][j] += cnt[i + 1][j] + cnt[i][j + 1] - cnt[i + 1][j + 1];
		}
	for(register int i = n; i; i--)
		for(register int j = n; j; j--)
		{
			f[i][j] = (cnt[i][j] == cnt[i + 1][j] ? f[i + 1][j] : sum[i][j] - a[j]);
			g[i][j] = (cnt[i][j] == cnt[i][j + 1] ? g[i][j + 1] : sum[i][j] - b[i]);
			a[j] = min(a[j] , g[i][j]) , b[i] = min(b[i] , f[i][j]);
		}
	printf("%lld" , f[1][1]);
}