Python数据科学手册-机器学习介绍

机器学习分为俩类： 有监督学习 supervised learning 和 无监督学习 unsupervised learning

• 有监督学习： 对数据的若干特征与若干标签之间 的关联性 进行建模的过程。 只要模型被确定，就可以应用到新的未知的数据上。
  
  进一步可以分为 分类 classification 任务 和 回归 regression 任务。
  
  分类任务： 标签是离散值。
  
  回归任务： 标签是连续值。

• 无监督学习： 指对不带任何标签的数据特征进行建模。 让数据自己介绍自己。 包括 聚类 clustering 任务 和 降维 dimensionality reduction 任务。
  
  聚类算法： 将数据分成不同组。
  
  降维算法：追求用更简洁的方式表现数据。

• 半监督 学习 semi-supervised learning 。介于有监督学习和无监督学习之间， 在数据标签不完整时使用。

Scikit-Learn 简介

Scikit-Learn 的 数据表示 data representation

机器学习是从数据创建模型的学问。 因此你首先需要了解咋样表示数据才能让计算机理解。 Scikit-Learn认为 是数据表。

数据表

鸢尾花 数据集



矩阵的行 称为 样本 samples. 行数记为 n_samples

每列数据表示每个样本 某个特征的量化值 。 矩阵的列 称为 特征 features 列数记为 n_features

• 特征矩阵。 features matrix
  
  通过二维数据或举证的形式将信息清晰地表达出来。
  
  间记为：X ,维度为 【n_samples, n_features】的 二维矩阵。一般用NumPy数组或Pandas 的DataFrame来表示。

• 目标数据
  
  需要一个标签 或 目标数组，通常 简记为 y
  
  目标数组 一般是 一维数组。 长度就是样本总数 n_samples.

对数据进行可视化

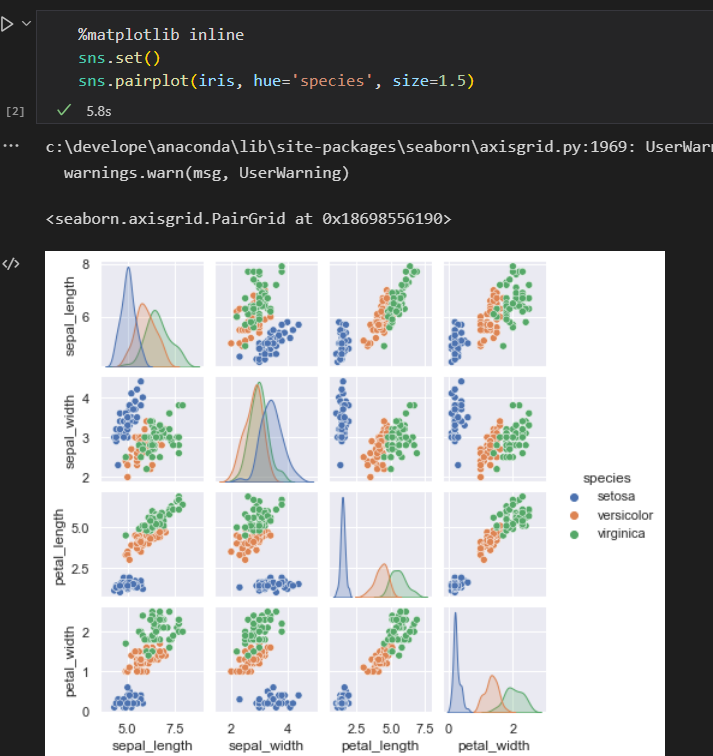
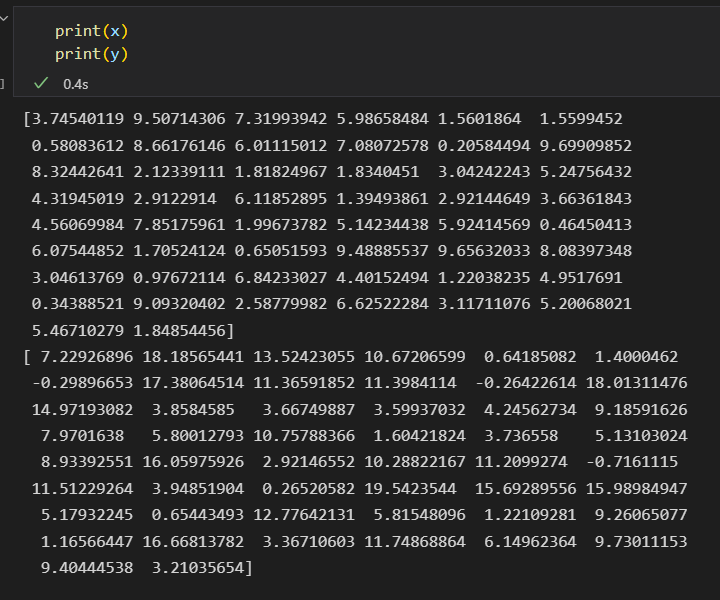
• 抽取特征矩阵 和目标数组
  
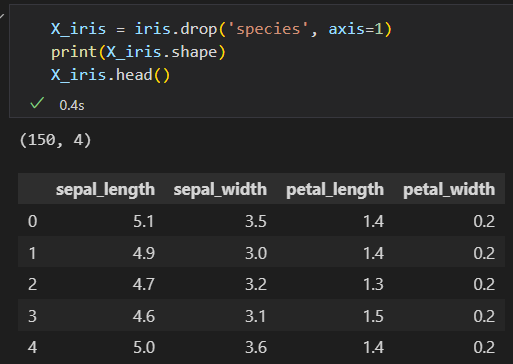
  特征矩阵如下
  
  
  
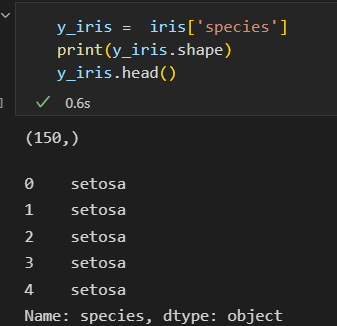
  目标数组如下
  
  

Scikit-Learn 的评估器API

设计原则：

• 统一性
  
  所有对象使用共同接口连接一组方法和统一文档
• 内省
  
  所有参数值都是公共属性
• 限制对象层级
  
  只有算法可以用python类表示。数据集都用标准数据类型 Numpy数组 DataFrame Scipy稀疏矩阵表示。 参数名称 用标准的Python字符串。
• 函数组合
• 明智的默认值

API基础知识

常用步骤如下

1）从Scikit-Learn 导入适当的评估器类， 选择模型类。

2）用合适 的数值对模型类 进行实例化，配置模型超参数 hyperparameter

3) 整理数据，获取 特征矩阵和 目标数组。

4） 调用模型实例 的fit()方法对数据进行 拟合

5）对新数据应用模型。

• 有监督学习模型中： 通常使用predict()方法预测新数据的标签
• 无监督学习模型中： 通常使用transform() 或 predict() 方法转换 或 推断数据的性质

有监督学习实例：简单线性回归。

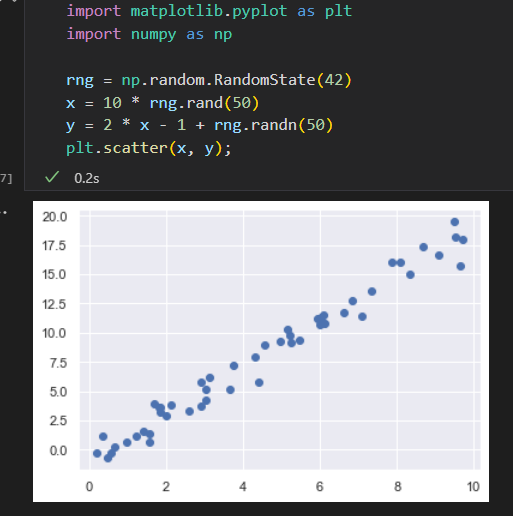
1）选择模型类

每个模型类都是一个Python类。 简单的线性回归模型。 直接导入 线性回归模型类

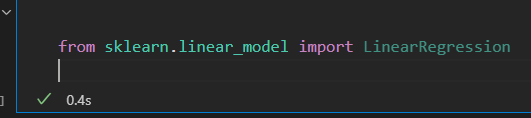
2）选择模型超参数

选择了模型之后，需要配置参数。



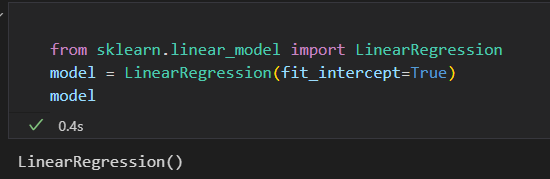
3）将数据整理成特征矩阵 和 目标数组

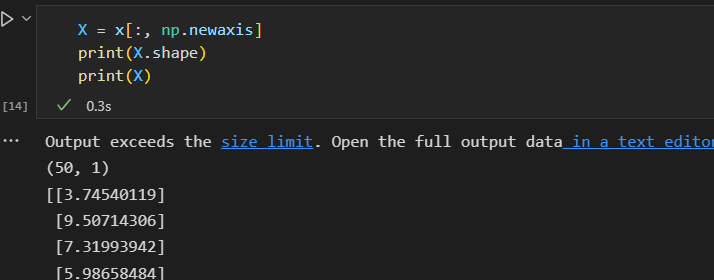
4）用模型拟合数据

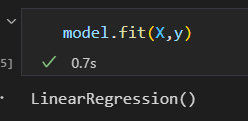
fit()方法获取的 模型参数都带一条下划线。





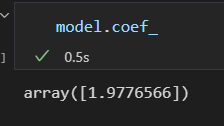
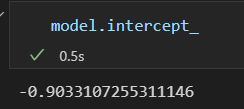
这俩个参数分别表示 对 样本数据 拟合直线的 斜率 和 截距 。

5）预测新数据的标签





预测



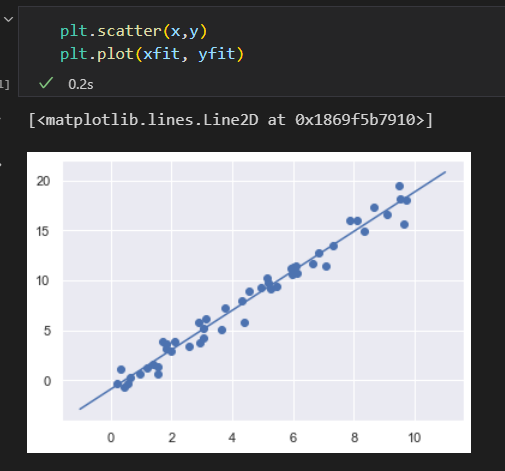
原始数据 和 拟合记过可视化

有监督学习示例：鸢尾花数据分类

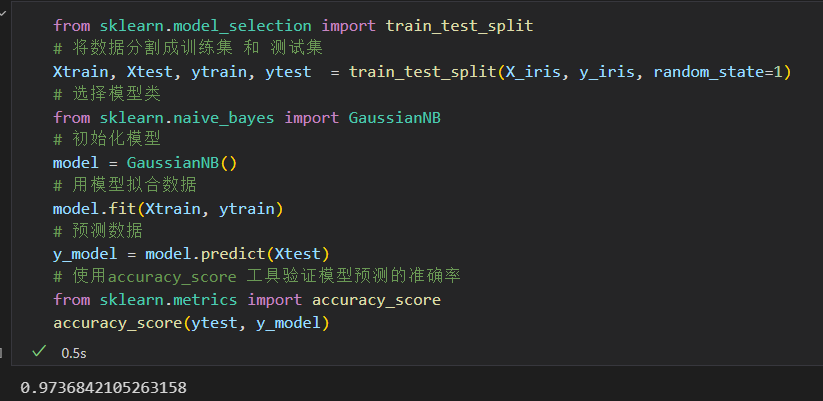
无监督学习示例：鸢尾花数据降维

对鸢尾花数据进行降维，以便更方便的对数据进行可视化，

降维的任务是要找到一个可以保留数据本质特征的 低维 矩阵来表示高维 数据。

使用 主成分 分析方法 PCA principal component analysis . 是一个快速线性降维技术。

用模型返回俩个主成分。 用二维数据表示 鸢尾花的思维数据。

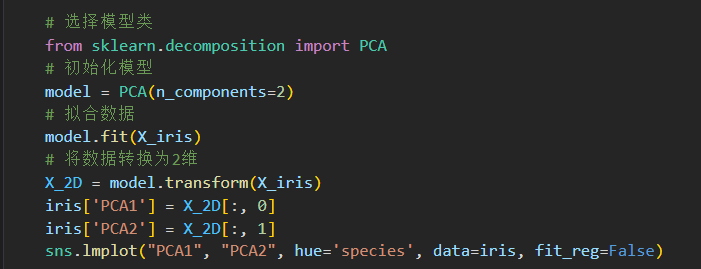
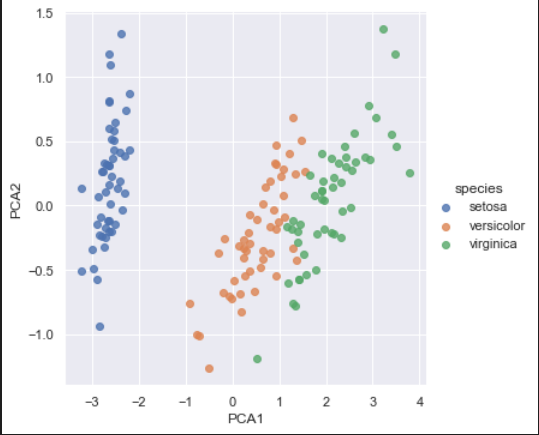
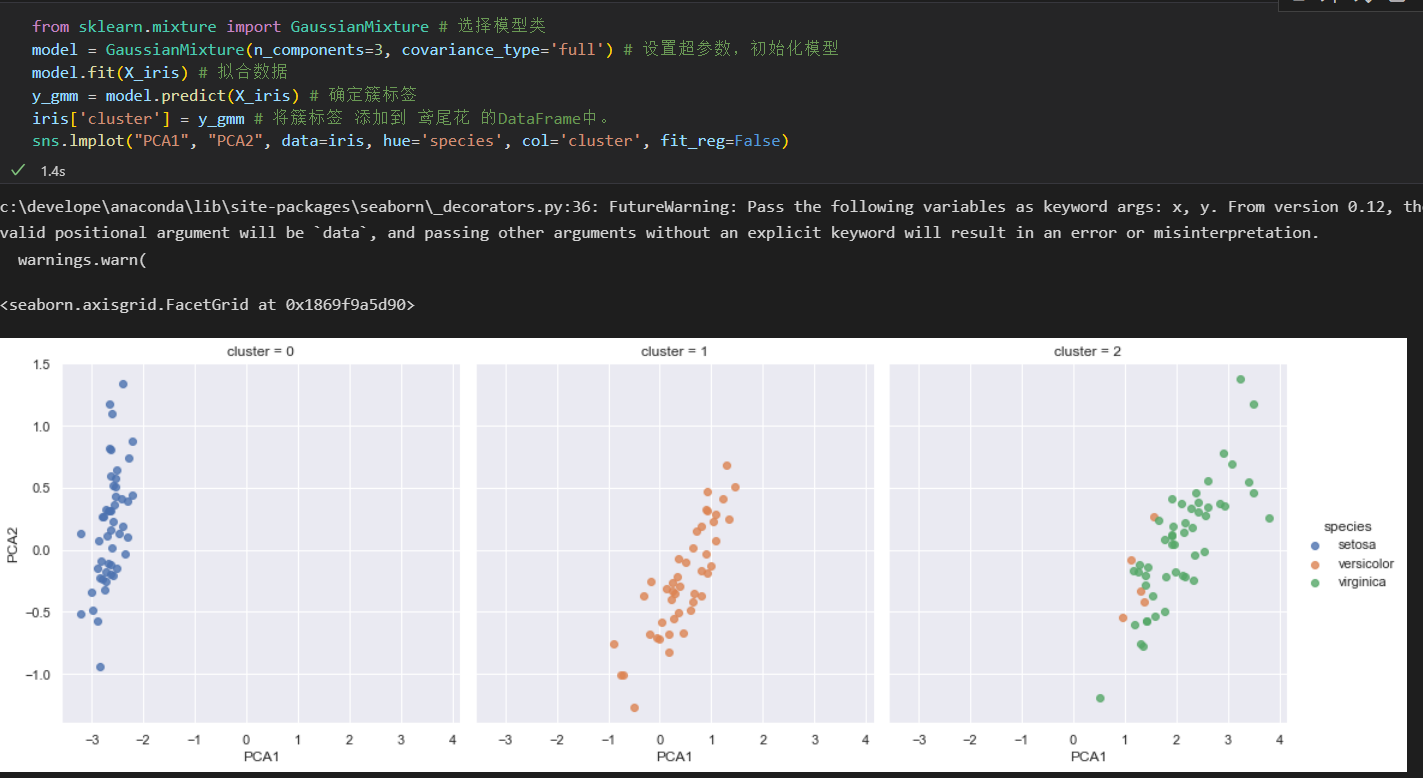
无监督学习示例： 鸢尾花数据聚类

聚类算法是要对没有任何标签的数据集 进行分组。

使用一个强大的聚类方法-高斯混合模型 Gaussian mixture model GMM

GMM 模型 试图将数据构造成若干服从高斯分布的概率密度函数簇。

手写数字探索。

加载并可视化手写数字

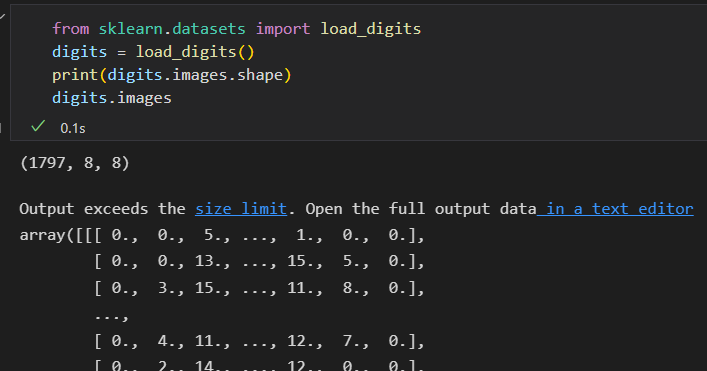
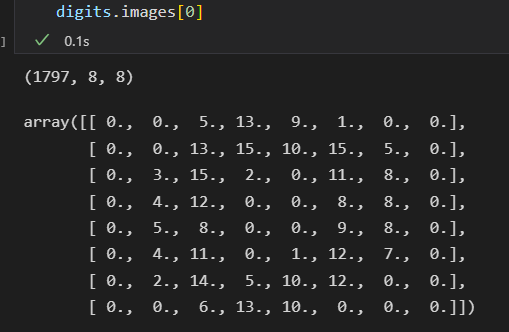
每张图像是 8 * 8 像素

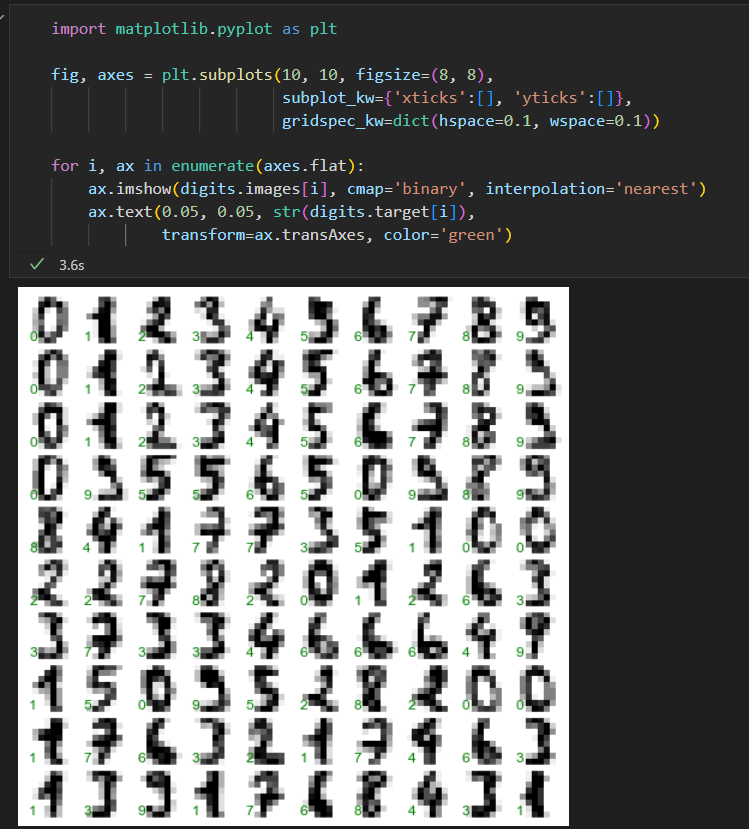
前一百张图可视化

为了在Scikit-Learn中使用数据，需要一个维度为【n_samples, n_features】的二维特征居住证。 可以将每个样本独享的所有像素作为特征。 8*8 = 64 个特征。 平铺成长度为64 的 一维数组。

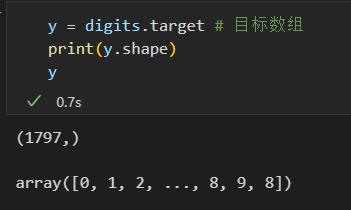
目标数组：表示每个数字的真实值。

无监督学习：降维

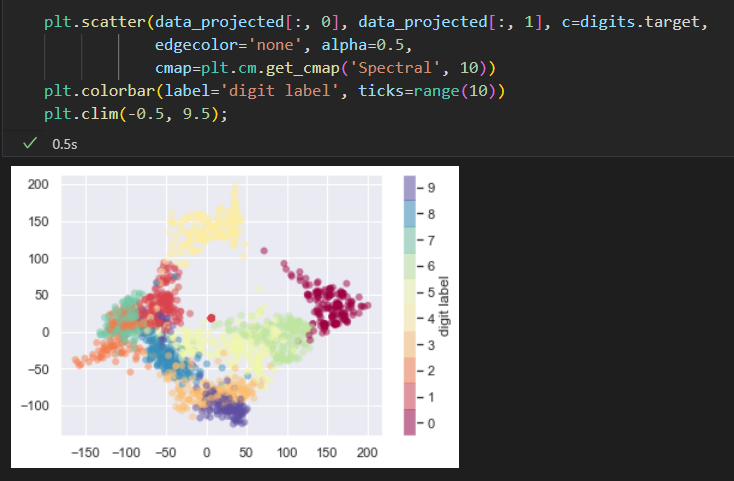
对64维参数进行可视化十分困难。 需要建筑 无监督学习方法将维度 降到 二维。

使用流形学习算法中的 lsomap 对数据进行降维

可视化

数字分类

找到一个分类算法，对手写数字进行分类。

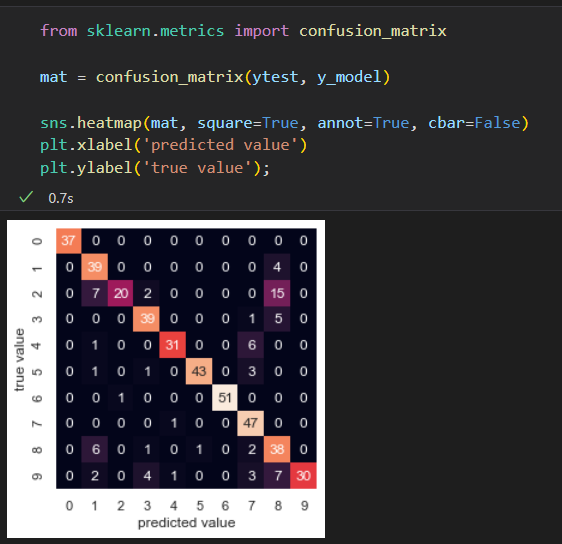
使用混淆矩阵 看哪里做的不好