「LOJ#10056」「一本通 2.3 练习 5」The XOR-longest Path （Trie

#10056. 「一本通 2.3 练习 5」The XOR-longest Path

题目描述

原题来自：POJ 3764

给定一棵 nnn 个点的带权树，求树上最长的异或和路径。

输入格式

第一行一个整数 nnn，接下来 n−1n-1n−1 行每行三个整数 u,v,wu,v,wu,v,w，表示 u,vu,vu,v 之间有一条长度为 www 的边。

输出格式

输出一行一个整数，表示答案。

样例

样例输入

4
1 2 3
2 3 4
2 4 6

样例输出

7

样例解释

最长的异或和路径是 1→2→31\to 2\to 31→2→3 ，它的长度是 3⨁4=73 \bigoplus 4=73⨁4=7。

注意：结点下标从 111 开始到 NNN。

注：x⨁yx \bigoplus yx⨁y 表示 xxx 与 yyy 按位异或。

数据范围与提示

对于 100%100\%100% 的数据，1≤n≤105,1≤u,v≤n,0≤w<2311\le n\le 10^5,1\le u, v \le n,0 \le w < 2^{31}1≤n≤10​5​​,1≤u,v≤n,0≤w<2​31​​

题解

首先对于树上两点路径的异或值，可以用一个树上前缀和维护。

记$sum[x]$为$x$到祖先的异或和。

由于异或有：$a ⨁ a = 0$

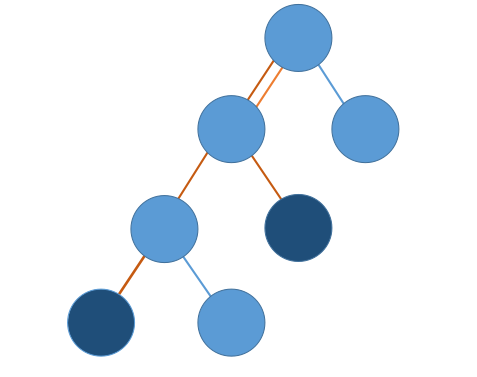
所以如下图，在$sum[u] ⨁ sum[v]$时，lca以上的屎色线已经被消掉了。

所以$ans=sum[u] ⨁ sum[v]$

问题转化为：有1e5个数，要求其中两数异或的最大值。

于是变为「LOJ#10050」「一本通 2.3 例 2」The XOR Largest Pair （Trie

于是这道题就可以由两道看起来离得很远的题拼起来而成了。

 编号     题目     状态     分数     总时间     内存     代码 / 答案文件     提交者     提交时间
 #     #. 「一本通 2.3 练习 」The XOR-longest Path    Accepted           ms      KiB     C++ / 1.8 K     qwerta     -- ::
 
 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 inline int read()
 {
     char ch=getchar();
     int x=;
     while(!isdigit(ch))ch=getchar();
     while(isdigit(ch)){x=x*+ch-'';ch=getchar();}
     return x;
 }
 const int MAXN=1e5+;
 struct emm{
     int e,f,v;
 }a[*MAXN];//用来建树
 int h[MAXN];
 int tot=;
 void con(int x,int y,int l)//连树边
 {
     a[++tot].f=h[x];
     h[x]=tot;
     a[tot].e=y;
     a[tot].v=l;
     a[++tot].f=h[y];
     h[y]=tot;
     a[tot].e=x;
     a[tot].v=l;
     return;
 }
 int d[MAXN],w[MAXN];//记深度和前缀和
 void dfs(int x)//dfs遍历树
 {
     for(int i=h[x];i;i=a[i].f)
     if(!d[a[i].e])
     {
         w[a[i].e]=(w[x] xor a[i].v);
         d[a[i].e]=d[x]+;
         dfs(a[i].e);
     }
     return;
 }
 struct ahh{
     int nxt[];
 }tr[];//Trie树
 int cnt=;
 int b[];//用来按位拆分
 void add(int x)
 {
     int j=-;
     memset(b,,sizeof(b));
     while(x)//拆二进制
     {
         b[++j]=x&;
         x>>=;
     }
     int k=;
     for(int j=;j>=;--j)
     {
         if(!tr[k].nxt[b[j]])
           tr[k].nxt[b[j]]=++cnt;
         k=tr[k].nxt[b[j]];
     }
     return;
 }
 long long find(int x)//返回与x异或的最大结果
 {
     int j=-;
     memset(b,,sizeof(b));
     while(x)
     {
         b[++j]=x&;
         x>>=;
     }
     long long now=;
     int k=;
     for(int j=;j>=;--j)
     {
         if(tr[k].nxt[-b[j]])//尽量往不一样的走
         {
             now+=(<<j);
             k=tr[k].nxt[-b[j]];
         }
         else k=tr[k].nxt[b[j]];
     }
     return now;
 }
 int main()
 {
     //freopen("a.in","r",stdin);
     int n=read();
     for(int i=;i<n;++i)
     {
         int u=read(),v=read(),w=read();
         con(u,v,w);//连树边
     }
     int s=min(,n);
     d[s]=;
     dfs(s);
     long long ans=;
     for(int i=;i<=n;++i)
       add(w[i]);//加前缀和
     for(int i=;i<=n;++i)
       ans=max(ans,find(w[i]));//记录答案
     cout<<ans;
     return ;
 }