简单的以下面曲线拟合例子来讲：

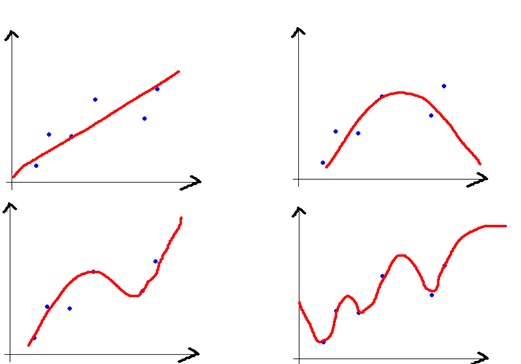
直线拟合后，相比原来的点偏差最大，最后一个图完全拟合了数据点偏差最小；但是拿第一个直线模型去预测未知数据，可能会相比最后一个模型更准确，因为最后一个模型过拟合了，即第一个模型的方差比最后一个模型小。一般而言高偏差意味着欠拟合，高方差意味着过拟合。他们之间有如下的关系：              本文地址

                                          

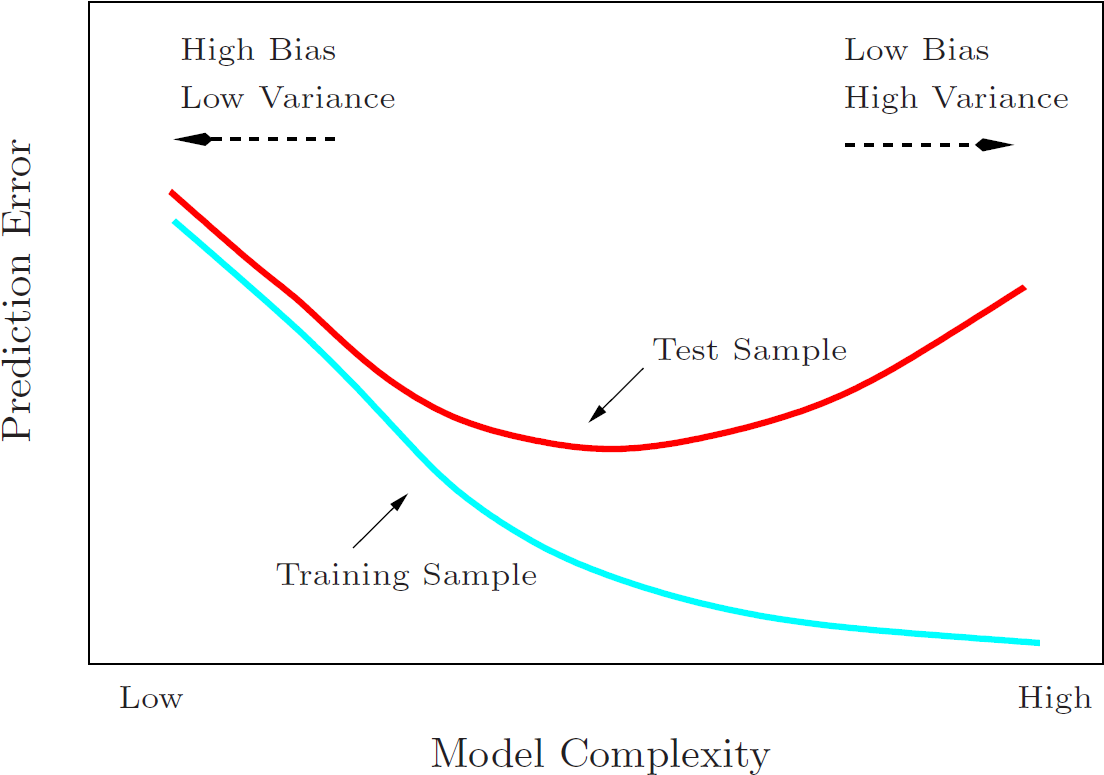
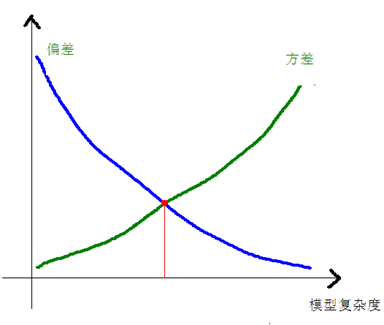
请参考一下三篇文章：

机器学习中的数学(2)-线性回归，偏差、方差权衡

Bias-Variance Tradeoff

偏差-方差分解 Bias-Variance Decomposition

【版权声明】转载请注明出处：http://www.cnblogs.com/TenosDoIt/p/3712590.html

机器学习算法中的偏差-方差权衡(Bias-Variance Tradeoff)的更多相关文章

  1. 【笔记】偏差方差权衡 Bias Variance Trade off

    偏差方差权衡 Bias Variance Trade off 什么叫偏差,什么叫方差 根据下图来说 偏差可以看作为左下角的图片,意思就是目标为红点,但是没有一个命中,所有的点都偏离了 方差可以看作为右 ...

  2. 偏差和方差以及偏差方差权衡(Bias Variance Trade off)

    当我们在机器学习领域进行模型训练时,出现的误差是如何分类的? 我们首先来看一下,什么叫偏差(Bias),什么叫方差(Variance): 这是一张常见的靶心图 可以看左下角的这一张图,如果我们的目标是 ...

  3. 训练/验证/测试集设置;偏差/方差;high bias/variance;正则化;为什么正则化可以减小过拟合

    1. 训练.验证.测试集 对于一个需要解决的问题的样本数据,在建立模型的过程中,我们会将问题的data划分为以下几个部分: 训练集(train set):用训练集对算法或模型进行训练过程: 验证集(d ...

  4. [转]理解 Bias 与 Variance 之间的权衡----------bias variance tradeoff

    有监督学习中,预测误差的来源主要有两部分,分别为 bias 与 variance,模型的性能取决于 bias 与 variance 的 tradeoff ,理解 bias 与 variance 有助于 ...

  5. 机器学习：偏差方差权衡（Bias Variance Trade off）

    一.什么是偏差和方差 偏差(Bias):结果偏离目标位置: 方差(Variance):数据的分布状态,数据分布越集中方差越低,越分散方差越高: 在机器学习中,实际要训练模型用来解决一个问题,问题本身可 ...

  6. 机器学习算法中如何选取超参数：学习速率、正则项系数、minibatch size

    机器学习算法中如何选取超参数:学习速率.正则项系数.minibatch size 本文是<Neural networks and deep learning>概览 中第三章的一部分,讲机器 ...

  7. 机器学习算法中的准确率(Precision)、召回率(Recall)、F值(F-Measure)

    摘要: 数据挖掘.机器学习和推荐系统中的评测指标—准确率(Precision).召回率(Recall).F值(F-Measure)简介. 引言: 在机器学习.数据挖掘.推荐系统完成建模之后,需要对模型 ...

  8. 机器学习算法中怎样选取超參数：学习速率、正则项系数、minibatch size

    本文是<Neural networks and deep learning>概览 中第三章的一部分,讲机器学习算法中,怎样选取初始的超參数的值.(本文会不断补充) 学习速率(learnin ...

  9. 机器学习总结-bias–variance tradeoff

    bias–variance tradeoff 通过机器学习,我们可以从历史数据学到一个\(f\),使得对新的数据\(x\),可以利用学到的\(f\)得到输出值\(f(x)\).设我们不知道的真实的\( ...

随机推荐

  1. Luogu P4944 【PION贪吃蛇】

    简单模拟题 用一个数据结构存储这条蛇 考虑蛇的移动 1,如果死了,就把整个蛇清空,所有位置标记为食物 2,如果吃了东西,把这个位置更新为蛇头 3,如果正常走路,这个位置设为蛇头,同时删掉尾巴 蛇的存储 ...

  2. DOM树示意图

  3. 【C++ Primer 第16章】2. 模板实参推断

    模板实参推断:对于函数模板,编译器利用调用中的函数实参来确定模板参数,从函数实参来确定模板参数的过程被称为模板实参推断. 类型转换与模板类型参数 与往常一样,顶层const无论在形参中还是在是实参中, ...

  4. 详解如何进行第三方App接入微信登录

    微信登录接入 微信登录遵循协议Aouth2.0中的授权码模式 我们来看一下Aouth2.0中的授权码模式是怎么定义的: 授权码模式(authorization code)是功能最完整.流程最严密的授权 ...

  5. Mybatis insert时返回自增id

    SelectKey在Mybatis中是为了解决Insert数据时不支持主键自动生成的问题,他可以很随意的设置生成主键的方式. 详细看这里:http://www.cnblogs.com/SimonHu1 ...

  6. 类属性判断 hasattr getattr

  7. js和css

    body{height:100%;background-image:url(./img/background.png);}  宽度同理 body的高度适应屏幕大小设置成  height:100%; 前 ...

  8. 《Gradle权威指南》--Android Gradle NDK支持

    No1: 在根项目下的local.properties文件中配置 sdk.dir=/home/frame/android/android-sdk ndk.dir=/home/frame/android ...

  9. Python打包方法——Pyinstaller (转)

      Python版本:Python3.5.2 一.安装Pyinstaller 1.安装pywin32 下载安装文件:查找到跟自己适用的python版本及window系统版本匹配的pywin32,下载后 ...

  10. grant 权限 on 数据库对象 to 用户

    grant 权限 on 数据库对象 to 用户 一.grant 普通数据用户,查询.插入.更新.删除 数据库中所有表数据的权利. grant select on testdb.* to common_ ...