机器学习-随机梯度下降（Stochastic gradient descent）和 批量梯度下降（Batch gradient descent ）

梯度下降（GD）是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种迭代求解思路，下面从公式和实现的角度对两者进行分析，如有哪个方面写的不对，希望网友纠正。

下面的h(x)是要拟合的函数，J(theta)损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数，i是参数的个数。

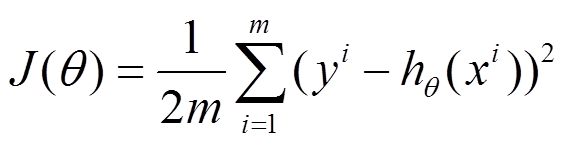
1、批量梯度下降的求解思路如下：

（1）将J(theta)对theta求偏导，得到每个theta对应的的梯度

（2）由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta

（3）从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度！！所以，这就引入了另外一种方法，随机梯度下降。

2、随机梯度下降的求解思路如下：

（1）上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

（2）每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta

（3）随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

3、对于上面的linear regression问题，与批量梯度下降对比，随机梯度下降求解的会是最优解吗？

（1）批量梯度下降---最小化所有训练样本的损失函数，使得最终求解的是全局的最优解，即求解的参数是使得风险函数最小。

（2）随机梯度下降---最小化每条样本的损失函数，虽然不是每次迭代得到的损失函数都向着全局最优方向， 但是大的整体的方向是向全局最优解的，最终的结果往往是在全局最优解附近。

4、梯度下降用来求最优解，哪些问题可以求得全局最优？哪些问题可能局部最优解？

对于上面的linear regression问题，最优化问题对theta的分布是unimodal，即从图形上面看只有一个peak，所以梯度下降最终求得的是全局最优解。然而对于multimodal的问题，因为存在多个peak值，很有可能梯度下降的最终结果是局部最优。

5、随机梯度和批量梯度的实现差别

以前一篇博文中NMF实现为例，列出两者的实现差别（注：其实对应Python的代码要直观的多，以后要练习多写python！）

    // 随机梯度下降，更新参数
    public void updatePQ_stochastic(double alpha, double beta) {
        for (int i = 0; i < M; i++) {
            ArrayList<Feature> Ri = this.dataset.getDataAt(i).getAllFeature();
            for (Feature Rij : Ri) {
                // eij=Rij.weight-PQ for updating P and Q
                double PQ = 0;
                for (int k = 0; k < K; k++) {
                    PQ += P[i][k] * Q[k][Rij.dim];
                }
                double eij = Rij.weight - PQ;  
 
                // update Pik and Qkj
                for (int k = 0; k < K; k++) {
                    double oldPik = P[i][k];
                    P[i][k] += alpha
                            * (2 * eij * Q[k][Rij.dim] - beta * P[i][k]);
                    Q[k][Rij.dim] += alpha
                            * (2 * eij * oldPik - beta * Q[k][Rij.dim]);
                }
            }
        }
    }  
 
    // 批量梯度下降，更新参数
    public void updatePQ_batch(double alpha, double beta) {  
 
        for (int i = 0; i < M; i++) {
            ArrayList<Feature> Ri = this.dataset.getDataAt(i).getAllFeature();  
 
            for (Feature Rij : Ri) {
                // Rij.error=Rij.weight-PQ for updating P and Q
                double PQ = 0;
                for (int k = 0; k < K; k++) {
                    PQ += P[i][k] * Q[k][Rij.dim];
                }
                Rij.error = Rij.weight - PQ;
            }
        }  
 
        for (int i = 0; i < M; i++) {
            ArrayList<Feature> Ri = this.dataset.getDataAt(i).getAllFeature();
            for (Feature Rij : Ri) {
                for (int k = 0; k < K; k++) {
                    // 对参数更新的累积项
                    double eq_sum = 0;
                    double ep_sum = 0;  
 
                    for (int ki = 0; ki < M; ki++) {// 固定k和j之后,对所有i项加和
                        ArrayList<Feature> tmp = this.dataset.getDataAt(i).getAllFeature();
                        for (Feature Rj : tmp) {
                            if (Rj.dim == Rij.dim)
                                ep_sum += P[ki][k] * Rj.error;
                        }
                    }
                    for (Feature Rj : Ri) {// 固定k和i之后,对多有j项加和
                        eq_sum += Rj.error * Q[k][Rj.dim];
                    }  
 
                    // 对参数更新
                    P[i][k] += alpha * (2 * eq_sum - beta * P[i][k]);
                    Q[k][Rij.dim] += alpha * (2 * ep_sum - beta * Q[k][Rij.dim]);
                }
            }
        }
    }