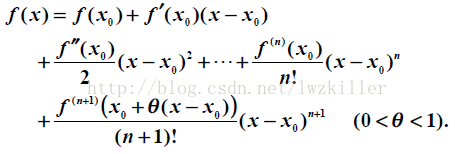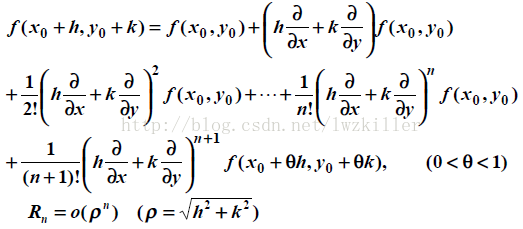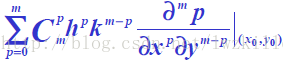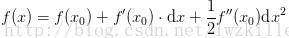hession矩阵的计算与在图像中的应用
参考的一篇博客,文章地址:https://blog.csdn.net/lwzkiller/article/details/55050275
Hessian Matrix,它有着广泛的应用,如在牛顿方法、求极值以及边缘检测、消除边缘响应等方面的应用。一个Hessian Matrix涉及到很多数学相关的知识点,比如泰勒公式、极值判断、矩阵特征值及特征向量、二次型等。本篇文章,主要说明多元情况下的极值判定、hessian矩阵与二次型的联系以及有关hessian matrix在图像上的应用。
1. 二元函数泰勒公式
对于一元函数的泰勒公式,大家都有所了解,其意义是使用多次多项式来近似表达原函数f(x),一元函数的f(x)的泰勒公式如下:
在实际应用中,我们一般取前面几阶多项式的和来近似表达原函数f(x)。
然而,在图像处理中,我们应用的都是二元函数f(x,y),下面着重讲解下二元函数的泰勒公式:
如果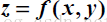
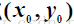

其中记号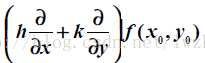
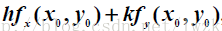
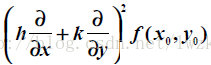
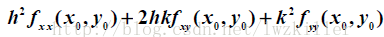
通用记号
人生苦短,关于这些公式这里就不证明了,大家可以参考相关数学资料进行证明。
2. 极值判断
如果对于函数中某一点其一阶导数为0,二阶导数不为0,那么该点必定为极值点。再进一步分析,如果二阶导数大于0,那么该点为极小值点,如果二阶导数小于0,那么该点为极大值点。关于这些性质的描述,最直观方法就是自己画图进行理解。另外可以通过表达式给予一些直观理解(省略后面的多阶余项),虽然表达式并非严格,比如,对于一元函数进行泰勒公式展开并认定完全相等:
针对凸函数,如果在x0处的一阶为0,二阶为正,那么我们就可以断定f(x)肯定比在x0处的函数值大,我们可以认为x0为极小值点。对于图像中的二元函数呢?我们是可以类推的。根据上述二元泰勒公式可得二阶近似表达式:
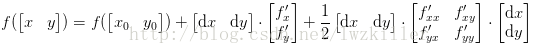
对于这种情形,这里面会涉及到Hessian矩阵正定以及负定的判断,这里令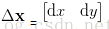

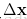
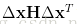
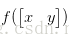

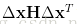
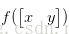
3. 二次型的性质
可以发现上面矩阵H即为Hessian矩阵,具有对称性。而二次型的矩阵也是对称的,接下来主要介绍下二次型最优化,以一个具体例子进行说明。
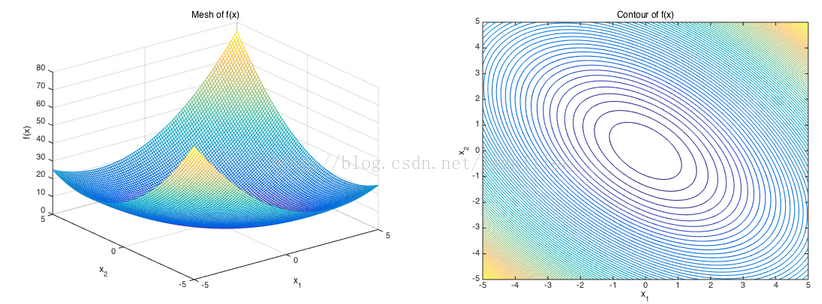
最小化二次型函数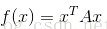
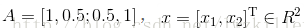
并且我们求得矩阵A的特征向量[-0.7071,0.7071],[0.7071,0.7071],对应的特征值分别为0.5,1.5
我们可以知道等高线越密集的地方,说明函数值变化较快,而这个函数变化最快的方向即是特征向量[0.7071,0.7071]所对应的方向;等高线越稀疏的地方,说明函数值变化较慢,而变化最慢的方向即是特征向量[-0.7071,0.7071]所对应的方向,并且可以观察矩阵特征值的大小与函数值变化程度有关,较大特征值所对应的特征向量方向上的函数值变化最快,较小特征值所对应的特征向量方向上的函数值变化最慢。
这里描述二次型的目的就是讲解Hessian矩阵的特征值以及特征向量与二次型函数值变化之间的关系。其中二次型函数的二阶偏导就构成了Hessian矩阵,也即是A矩阵。
4. 边缘检测以及边缘响应消除
既然检测到的对应点确认为边缘点,那么我们就有理由消除这个边缘点,所以边缘检测与边缘响应消除的应用是一回事。边缘到底有什么特征呢?如下图所示,一个二维平面上的一条直线,图像的特征具体可以描述为:沿着直线方向,亮度变化极小,垂直于直线方向,亮度由暗变亮,再由亮变暗,沿着这个方向,亮度变化很大。我们可以将边缘图像分布特征与二次型函数图形进行类比,是不是发现很相似,我们可以找到两个方向,一个方向图像梯度变化最慢,另一个方向图像梯度变化最快。那么图像中的边缘特征就与二次型函数的图像对应起来了,其实二次型函数中的hessian矩阵,也是通过对二次型函数进行二阶偏导得到的(可以自己求偏导测试下),这就是我们为什么可以使用hessian矩阵来对边缘进行检测以及进行边缘响应消除,我想大家应该明白其中的缘由了。还是那句话,数学模型其实就是一种反映图像特征的模型。
所以Hessian matrix实际上就是多变量情形下的二阶导数,他描述了各方向上灰度梯度变化,这句话应该很好理解了吧。我们在使用对应点的hessian矩阵求取的特征向量以及对应的特征值,较大特征值所对应的特征向量是垂直于直线的,较小特征值对应的特征向量是沿着直线方向的。对于SIFT算法中的边缘响应的消除可以根据hessian矩阵进行判定。
关于hessian的应用基本讲完了,有问题可以留言讨论。
参考文献:
1.https://www.zhihu.com/question/40181086
2.https://zh.wikipedia.org/wiki/%E6%B5%B7%E6%A3%AE%E7%9F%A9%E9%98%B5
3.http://www.zhihujingxuan.com/18143.html
4.http://blog.sina.cn/dpool/blog/s/blog_5d2990b70101c1pc.html
5.http://blog.sina.com.cn/s/blog_790bb71901015087.html
6.http://painterlin.com/2015/09/12/Intuition-of-Eigen-Value.html
hession矩阵的计算与在图像中的应用的更多相关文章
- OpenCV,计算两幅图像的单应矩阵
平面射影变换是关于其次3维矢量的一种线性变换,可以使用一个非奇异的$3 \times 3$矩阵H表示,$X' = HX$,射影变换也叫做单应(Homography).计算出两幅图像之间的单应矩阵H,那 ...
- OpenGL中摄像机矩阵的计算原理
熟悉OpenGL|ES的朋友,可能会经常设置摄像机的view矩阵,iOS中相对较好,已经封装了方向,只需要设置摄像机位置,目标点位置以及UP向量即可.下面先介绍下摄像机view矩阵的计算原理.此处假设 ...
- Matlab实现Hough变换检測图像中的直线
Hough变换的原理: 将图像从图像空间变换至參数空间.变换公式例如以下: 变换以后,图像空间与參数空间存在下面关系: 图像空间中的一点在參数空间是一条曲线,而图像空间共线的各点相应于參数空间交于一点 ...
- 【OpenCV学习】计算两幅图像的重叠区域
问题描述:已知两幅图像Image1和Image2,计算出两幅图像的重叠区域,并在Image1和Image2标识出重叠区域. 算法思想: 若两幅图像存在重叠区域,则进行图像匹配后,会得到一张完整的全景图 ...
- Halcon学习之六:获取Image图像中Region区域的特征参数
area_center_gray ( Regions, Image : : : Area, Row, Column ) 计算Image图像中Region区域的面积Area和重心(Row,Colu ...
- 【opencv学习笔记七】访问图像中的像素与图像亮度对比度调整
今天我们来看一下如何访问图像的像素,以及如何改变图像的亮度与对比度. 在之前我们先来看一下图像矩阵数据的排列方式.我们以一个简单的矩阵来说明: 对单通道图像排列如下: 对于双通道图像排列如下: 那么对 ...
- Matlab实现Hough变换检测图像中的直线 分类: 图像处理 2014-06-14 22:07 641人阅读 评论(0) 收藏
Hough变换的原理: 将图像从图像空间变换至参数空间,变换公式如下: 变换以后,图像空间与参数空间存在以下关系: 图像空间中的一点在参数空间是一条曲线,而图像空间共线的各点对应于参数空间交于一点的各 ...
- 从单一图像中提取文档图像:ICCV2019论文解读
从单一图像中提取文档图像:ICCV2019论文解读 DewarpNet: Single-Image Document Unwarping With Stacked 3D and 2D Regressi ...
- 访问图像中的像素[OpenCV 笔记16]
再更一发好久没更过的OpenCV,不过其实写到这个部分对计算机视觉算法有所了解的应该可以做到用什么查什么了,所以后面可能会更的慢一点吧,既然开了新坑,还是机器学习更有研究价值吧... 图像在内存中的存 ...
随机推荐
- Dubbo实践(九)ExtensionFactory
ExtensionLoader.java中注意到injectExtension函数是为了设置所生成的对象的field:其方法为对于有set函数的field进行设置.此时用到了ExtensionFact ...
- sharepoint rest 脚本发送邮件
function processSendEmails() { var from = 'asad@Example.com', to = 'someone@Example.com', body = 'He ...
- first-child伪类选择器
原文链接地址:https://www.cnblogs.com/wangmeijian/p/4562304.html :first-child 选择器用于选取属于其父元素的首个子元素的指定选择器.——w ...
- Docker 常用命令——容器
1.新建并启动容器 docker run [option] images [command][arg] #根据镜像新建容器并运行.如果本地没有镜像则从docker hub上拉取. --name ...
- webpack4.26的详细配置,包含babel, eslint, postcss, 及各种所需loader,内含大量注释
github地址:https://github.com/qianxiaoning/demo-webpack4.26 内含详尽注释 欢迎大家star或者fork呀~ 目录结构: completeDemo ...
- 水仙花数(类型:一级、C++)
题目描述: 输入一个三位数n,判断是否为水仙花数,如果是则输出“YES”,不是则输出“NO”.水仙花数:是指一个3位数,它的每个位上的数字的3次幂之和等于它本身.(例如:1^3 + 5^3+ 3^3 ...
- 傻瓜式搭建php+nginx+mysql服务器环境
1.安装nginx 1.安装yum源 rpm -Uvh http://nginx.org/packages/centos/7/noarch/RPMS/nginx-release-centos-7-0. ...
- py基础---多线程、多进程、协程
目录 Python基础__线程.进程.协程 1.什么是线程(thread)? 2.什么是进程(process)? 3.进程和线程的区别 4.GIL全局解释器锁 5.多线程(threading模块) 6 ...
- Windows.Devices API in a C# WinForm Win32 Desktop application in Windows 10
https://social.msdn.microsoft.com/Forums/windows/en-US/40b4f86d-b6d5-430e-a235-7fc003dec4c4/how-to-u ...
- IOS 可以连接 蓝牙BLE设备,但是无法发现服务(原创)
注:转载请标明文章来源,感谢支持作者劳动! 一.问题描述 用iphone手机上的nRF connect软件调试蓝牙通信. 1.nRF52蓝牙demo电路板,烧录一个SDK的程序,iphone手机可以成 ...