洛谷 P4009 汽车加油行驶问题 解题报告

P4009 汽车加油行驶问题

题目描述

给定一个\(N×N\)的方形网格，设其左上角为起点◎，坐标(1,1) ，\(X\)轴向右为正，\(Y\)轴向下为正，每个方格边长为1 ，如图所示。

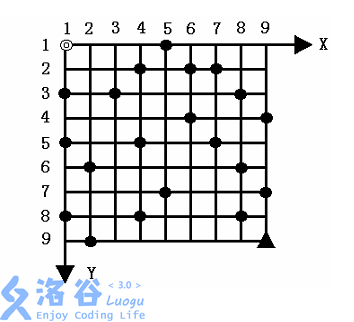
一辆汽车从起点◎出发驶向右下角终点▲，其坐标为\((N,N)\) 。

在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:

汽车只能沿网格边行驶，装满油后能行驶\(K\)条网格边。出发时汽车已装满油，在起点与终点处不设油库。

汽车经过一条网格边时，若其\(X\)坐标或\(Y\)坐标减小，则应付费用\(B\)，否则免付费用。

汽车在行驶过程中遇油库则应加满油并付加油费用\(A\) 。

在需要时可在网格点处增设油库，并付增设油库费用\(C\)(不含加油费用\(A\))。

\(N,K,A,B,C\)均为正整数， 且满足约束: \(2≤N≤100,2≤K≤10\) 。

设计一个算法，求出汽车从起点出发到达终点所付的最小费用。

输入输出格式

输入格式：

文件的第一行是 \(N,K,A,B,C\)的值。

第二行起是一个 \(N×N\)的0-1方阵,每行\(N\)个值,至\(N+1\)行结束。

方阵的第\(i\)行第\(j\)列处的值为1表示在网格交叉点\((i,j)\)处设置了一个油库,为\(0\)时表示未设油库。各行相邻两个数以空格分隔。

输出格式：

程序运行结束时,输出最小费用。

说明

\(2≤n≤100,2≤k≤10\)

---

据说是费用流，没看出来。连分层图都没看出来，胡乱打了个最短路偏分发现居然有强制消费。

分层图按\(k\)也就是走的步数来分层，但这里我打了优先队列BFS，本质上和disj最短路的思想是一样的，但似乎跑的慢一些？？

---

Code：

#include <cstdio>
#include <queue>
#include <cstring>
#include <cstdlib>
using namespace std;
const int N=103;
const int I[5]={0,0,1,0,-1};
const int J[5]={0,1,0,-1,0};
int n,k,a,b,c;//方格大小,可连边长，加油费，倒车费，开厂费
int used[N][N][12],g[N][N],cost[5];
void init()
{
    scanf("%d%d%d%d%d",&n,&k,&a,&b,&c);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&g[i][j]);
    cost[3]=cost[4]=b;
}
struct node
{
    int i,j,w,dep;
    node(){}
    node(int i,int j,int w,int dep)
    {
        this->i=i;
        this->j=j;
        this->w=w;
        this->dep=dep;
    }
    bool friend operator <(node n1,node n2)
    {
        return n1.w>n2.w;
    }
};
priority_queue <node > q;
void work()
{
    node t0(1,1,0,0);
    q.push(t0);
    while(!q.empty())
    {
        int ii=q.top().i,jj=q.top().j,dep=q.top().dep,w=q.top().w;
        q.pop();
        if(ii==n&&jj==n)
        {
            printf("%d\n",w);
            exit(0);
        }
        if(used[ii][jj][dep]) continue;
        used[ii][jj][dep]=1;
        for(int l=1;dep!=k&&l<=4;l++)
        {
            int i=ii+I[l],j=jj+J[l];
            if(i>n||i<1||j>n||j<1) continue;
            if(!g[i][j])
            {
                if(!used[i][j][dep+1])//直接走
                {
                    node tt(i,j,w+cost[l],dep+1);
                    q.push(tt);
                }
                if(!used[i][j][0]&&i!=n&&j!=n)//开工厂
                {
                    node tt(i,j,w+cost[l]+c+a,0);
                    q.push(tt);
                }
            }
            if(g[i][j]&&!used[i][j][0])//强制消费
            {
                node tt(i,j,w+cost[l]+a,0);
                q.push(tt);
            }

        }
    }
}
int main()
{
    init();
    work();
    return 0;
}

---

2018.7.5