C# winFrom 制作、打包、签名、发布Activex全过程

注：转自园中 http://www.cnblogs.com/still-windows7/p/3148623.html

一、前言

最近有这样一个需求，需要在网页上面启动客户端的软件，软件之间的通信、调用，单单依靠HTML是无法实现了，因此必须借用Activex来实现。由于本人主要擅长C#，自然本文给出了用C#实现的范例，本文的预期效果是有一定Winform基础的人可都轻松读懂本文。

文章主要介绍了以下几个部分：

 

1、用C#制作Activex控件，并发布为msi安装文件

 

2、将msi打包为cab，达到浏览器自动安装的效果

 

3、给cab数字签名（可选）

 

4、将Activex应用到网页上

 

二、用C#制作Activex控件，并发布为msi安装文件

 

1）新建window用户控件项目EasyActivex。其实VS2010并没有提供专门的Activex项目模板，所谓的Activex，只要符合com标准即可。

 

 

 

 

2）在EasyActivex项目添加IObjectSafety接口

 

 

在IObjectSafety接口代码如下，值得注意的是Guid不能随便改，必须为一下代码给出的Guid：

 

using System;
using System.Collections.Generic;
using System.Text;
using System.Runtime.InteropServices;

namespace EasyActivex
{

    [ComImport, GuidAttribute("CB5BDC81-93C1-11CF-8F20-00805F2CD064")]
    [InterfaceTypeAttribute(ComInterfaceType.InterfaceIsIUnknown)]
    public interface IObjectSafety
    {
        [PreserveSig]
        int GetInterfaceSafetyOptions(ref Guid riid, [MarshalAs(UnmanagedType.U4)] ref int pdwSupportedOptions, [MarshalAs(UnmanagedType.U4)] ref int pdwEnabledOptions);

        [PreserveSig()]
        int SetInterfaceSafetyOptions(ref Guid riid, [MarshalAs(UnmanagedType.U4)] int dwOptionSetMask, [MarshalAs(UnmanagedType.U4)] int dwEnabledOptions);
    }
}

3）在EasyActivex项目添加EUserControl控件，在控件中实现IObjectSafety接口。

 

 

在控件上面添加按钮，命名为btnOpenNote

 

 

控件的后台代码必须实现IObjectSafety接口

 

 

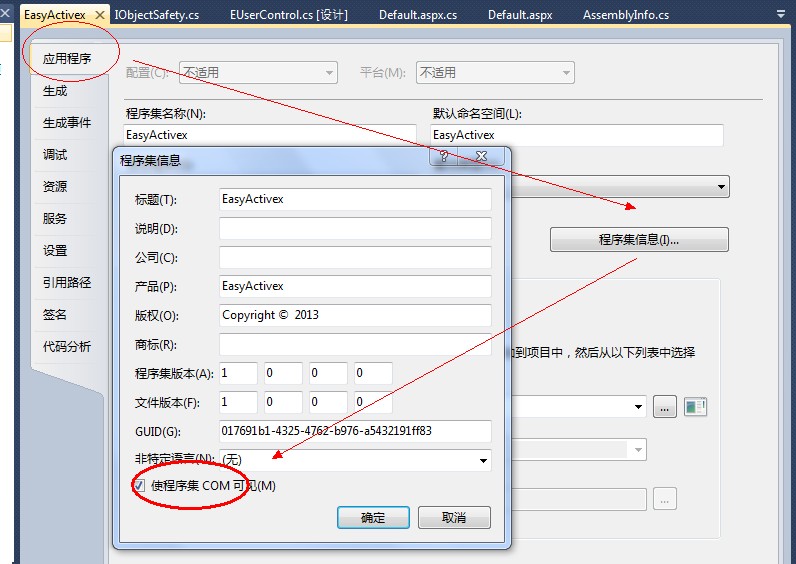
小提示：EUserControl代码的Guid可以用VS附带的Guid生成工具生成：

 

4）在EasyActivex项目AssemblyInfo.cs文件中添加代码

 

 

 

//用户添加
[assembly: AllowPartiallyTrustedCallers()]

5）设置EasyActivex项目项目属性为com互操作

 

 

6）新建windows程序安装项目EasySetup

 

 

7）将EasyActivex项目生产的dll添加到EasySetup项目中。下图的EasyActivex.dll为已经添加进去了的文件。

 

 

8）在EasySetup项目中，设置EasyActivex.dll文件属性为vsdraCOM。

 

 

完成以上步骤，生成下即可得到msi安装文件

 

三、将msi安装文件打包为cab，达到在浏览器中自动安装的效果

 

如果只是生成了msi文件，用户安装的时候比较麻烦，像安装一般软件一样，需要用户慢慢点击下一步，慢慢安装，在本项目中采用打包成cab文件的方式，做到用户点击运行后，即可自动安装。

在这里需要准备文件有：

    cabarc.exe：微软提供的cab打包工具

    EasySetup.msi：  本案例中EasySetup项目生成的windows部署安装文件

    install.inf ： 需要跟EasySetup.msi打包在一起的文件，制作方法请见下文

    build.bat：  打包的批处理命令，制作方法请见下文

 

1）  install.inf制作。新建txt文件，加入以下内容，将文件名重新命名为install.inf即可。其中EasyZSetup.msi即是要打包的安装程序的名称。

[version]
signature="$CHICAGO$"
AdvancedINF=2.0  

[Setup Hooks]
hook1=hook1  

[hook1]
run=msiexec.exe /i "%EXTRACT_DIR%\EasySetup.msi" /qn 

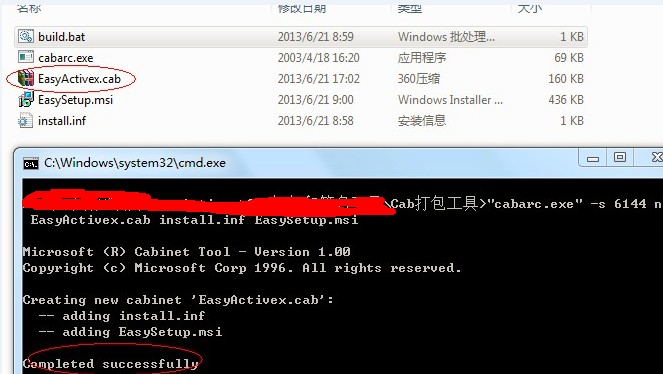
2）   build.bat制作。新建txt文件，加入以下内容，将文件名重新命名build.bat即可。其中EasyActivex.cab是生成目标cab的名称；install.inf是第一步生成的文件名，而EasySetup.msi是需要打包的安装程序名；第二条ping命令仅仅是让批处理不要那么快退出，起到更利于观察生成结果的作用。

"cabarc.exe" -s 6144 n EasyActivex.cab install.inf EasySetup.msi
ping -n 20 127.0.0.1 >nul 

 把以上四个文件复制到同一个文件夹中，双击build.bat批处理命令即可生成cab文件

 

 

双击bat后的运行结果如下，其中EasyActivex.cab即是生成的目标cab文件。

 

 

 

三、给cab数字签名（可选）

 

     由于处于安全问题考虑，IE浏览器设置默认是禁用未签名的Activex控件的，不过想想也知道，假如打开个未知网页，“网页”就能随便调用计算机本地的东西是多么恐怖的事情，因此，浏览器运行的Activex必须是签名了的，也符合常理。

     如果不怕用户麻烦，不采用cab签名的方式的话，也可以通过设置浏览器安全性来运行Activex。设置方法：打开浏览器--浏览器Internet选项--安全选项卡--自定义级别按钮-下载未签名的Activex控件设置为提示，保存即可。等安装完毕后，可以将“下载未签名的Activex控件”设置回禁用。

   以下为给cab签名的方法，具体方法，数字认证网上面已经介绍得很详细：

 

   1）申请、安装证书。上中国数字认证网（http://www.ca365.com/）申请一个免费数字证书（试用期为1年，如果企业用的话需要购买）。 

        操作方法：http://www.ca365.com/forward.do?pageurl=/ca/yhsc/4.jsp ，值得注意的是证书用途必须选择代码签名证书。

        申请成功后的证书，由于是不带密钥的，因此下载完毕后只能够在申请证书的机器上安装、使用（签名文件），如果需要在其他机器上使用的话需要将密钥导出，操作方法为： http://www.ca365.com/forward.do?pageurl=/ca/yhsc/5.jsp 。

 

  2）用证书给cab包签名：http://www.ca365.com/forward.do?pageurl=/ca/thsc/7.jsp 

 

四、在解决方案中添加EasyWeb项目

 

    终于到了最后一步，发布鸟。在解决方案中添加EasyWeb项目

 

 

 

在网页目录中新建Activex文件夹，并将EasyActivex.cab文件拷贝进去

 

 

在网页中添加以下代码，即可调用Activex控件了。值得注意的是codebase是cab包的相对路径；clsid是EUserControl控件的Guid。

 

 <object id="csharpActiveX" codebase="Activex/EasyActivex.cab" classid="clsid:685F0A47-944D-4145-BF4E-76A02A422B02"></object>

运行效果如下：

点击即可在网页中打开记事本了。

五、本案例源码+cab打包工具+数字签名工具下载

六、参考资料：

1、使用C#开发ActiveX控件  http://www.cnblogs.com/yilin/archive/2009/09/15/1567332.html

2、Activex签名方法和工具技巧  http://www.360doc.com/content/10/0901/15/203871_50402416.shtml

3、中国数字认证网用户手册 http://www.ca365.com/forward.do?pageurl=/ca/yhsc.jsp