分类算法SVM（支持向量机)

支持向量机（Support Vector Machine ,SVM）的主要思想是：建立一个最优决策超平面，使得该平面两侧距离该平面最近的两类样本之间的距离最大化，从而对分类问题提供良好的泛化能力。对于一个多维的样本集，系统随机产生一个超平面并不断移动，对样本进行分类，直到训练样本中属于不同类别的样本点正好位于该超平面的两侧，满足该条件的超平面可能有很多个，SVM正式在保证分类精度的同时，寻找到这样一个超平面，使得超平面两侧的空白区域最大化，从而实现对线性可分样本的最优分类。

支持向量机中的支持向量（Support Vector）是指训练样本集中的某些训练点，这些点最靠近分类决策面，是最难分类的数据点。SVM中最优分类标准就是这些点距离分类超平面的距离达到最大值；“机”（Machine）是机器学习领域对一些算法的统称，常把算法看做一个机器，或者学习函数。SVM是一种有监督的学习方法，主要针对小样本数据进行学习、分类和预测，类似的根据样本进行学习的方法还有决策树归纳算法等。

SVM的优点：

1、不需要很多样本，不需要有很多样本并不意味着训练样本的绝对量很少，而是说相对于其他训练分类算法比起来，同样的问题复杂度下，SVM需求的样本相对是较少的。并且由于SVM引入了核函数，所以对于高维的样本，SVM也能轻松应对。

2、结构风险最小。这种风险是指分类器对问题真实模型的逼近与问题真实解之间的累积误差。

3、非线性，是指SVM擅长应付样本数据线性不可分的情况，主要通过松弛变量（也叫惩罚变量）和核函数技术来实现，这一部分也正是SVM的精髓所在。

一、线性分类

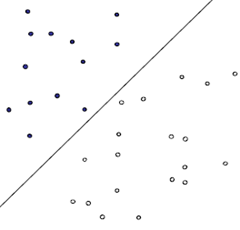
对于最简单的情况，在一个二维空间中，要求把下图所示的白色的点和黑色的点集分类，显然，下图中的这条直线可以满足我们的要求，并且这样的直线并不是唯一的。

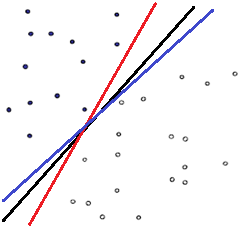
SVM的作用就是要查找到最合适的决策直线所在的位置。其他可行的直线可以如下所示：

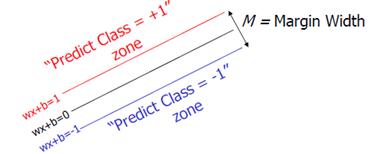
那么哪条直线才是最优的呢？就是分类两侧距离决策直线距离最近的点离该直线综合最远的那条直线，即分割的间隙越大越好，这样分出来的特征的精确性更高，容错空间也越大。这个过程在SVM中被称为最大间隔（Maximum Marginal）。下图红色和蓝色直线之间的间隙就是要最大化的间隔，显然在这种情况下，分类直线位于中间位置时可以使得最大间隔达到最大值。

二、 线性不可分

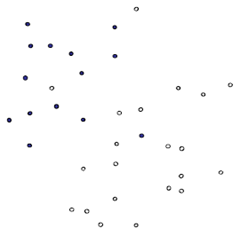
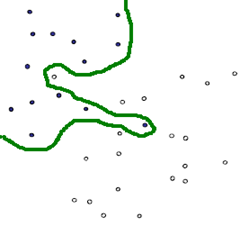
现实情况中基于上文中线性分类的情况并不具有代表性，更多情况下样本数据的分布式杂乱无章的，这种情况下，基于线性分类的直线分割面就无法准确完成分割。如下图，在黑色点集中掺杂有白色点，白色点集中掺杂有黑色点的情况：

对于这种非线性的情况，一种方法是使用一条曲线去完美分割样品集，如下图：

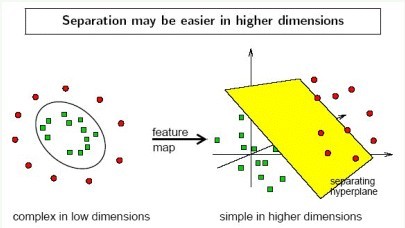
从二维空间扩展到多维，可以使用某种非线性的方法，让空间从原本的线性空间转换到另一个维度更高的空间，在这个高维的线性空间中，再用一个超平面对样本进行划分，这种情况下，相当于增加了不同样本间的区分度和区分条件。在这个过程中，核函数发挥了至关重要的作用，核函数的作用就是在保证不增加算法复杂度的情况下将完全不可分问题转化为可分或达到近似可分的状态。

上图左侧红色和绿色的点在二维空间中，绿色的点被红色点包围，线性不可分，但是扩展到三维（多维）空间后，可以看到，红绿色点间Z方向的距离有明显差别，同种类别间的点集有一个共同特征就是他们基本都在一个面上，所以借用这个区分，可以使用一个超平面对这两类样本进行分类，如上图中黄色的平面。

线性不可分映射到高维空间，可能导致很高的维度，特殊情况下可能达到无穷多维，这种情况下会导致计算复杂，伴随产生惊人的计算量。但是在SVM中，核函数的存在，使得运算仍然是在低维空间进行的，避免了在高维空间中复杂运算的时间消耗。

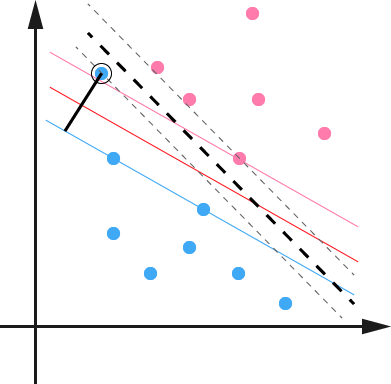
SVM另一个巧妙之处是加入了一个松弛变量来处理样本数据可能存在的噪声问题，如下图所示：

SVM允许数据点在一定程度上对超平面有所偏离，这个偏移量就是SVM算法中可以设置的outlier值，对应于上图中黑色实现的长度。松弛变量的加入使得SVM并非仅仅是追求局部效果最优，而是从样本数据分布的全局出发，统筹考量，正所谓成大事者不拘小节。