K好数--蓝桥杯

JAVA版K好数--蓝桥杯

历经千辛万苦，也算是研究出来了这道题了。

这道题主要运用了动态规划(Dynamic Planning)的思想，何谓动态规划？其实就是将一个大问题分成一个个小问题，然后先通过把各个小问题都解决，自然而然大问题也就解决了。

这道题它问L位K进制中，有多少K好数(任意相邻两位数字不相临)

---

我的理解： K进制的意思是它每一位的组成只能从(0~K-1)中选取，如果你想直接求L位长的K进制数有多少K好数，可能有些复杂，不如先求1位长，再通过1位长求2位长……以此类推，便可以通过累加得出L位长的K好数总共有多少。

先上代码

   public static void KGoodNumber() {
        Scanner sc = new Scanner(System.in);
        long mod = 1000000007;
        int radix = sc.nextInt();
        int length = sc.nextInt();
        long dp[][] = new long[length][jinzhi];
        //二维数组第一维是表示长度，第二维表示该长度下开头的数字，该数组的值为满足前二条件的K好数的个数
        for (int i = 0; i < radix; i++) {
            dp[0][i] = 1;
        }
        for (int m = 1; m < length; m++) {
            for (int j = 0; j < radix; j++) {
                for (int x = 0; x < radix; x++) {
                    if (x != j + 1 && x != j - 1) {
           				//如果m位长的开头为j，m-1位长开头为x，并且x与j不相临
                        ** dp[m][j] += dp[m - 1][x];
                           dp[m][j] %= mod;
                    }
                }
            }
        }
        long sum = 0;
        //由于K好数不能以0开头，所以从1开始取
        for (int y = 1; y < radix; y++) {
            sum += dp[length - 1][y];
            sum %= mod;
        }
        System.out.println(sum);
    }

上个图来解释一下

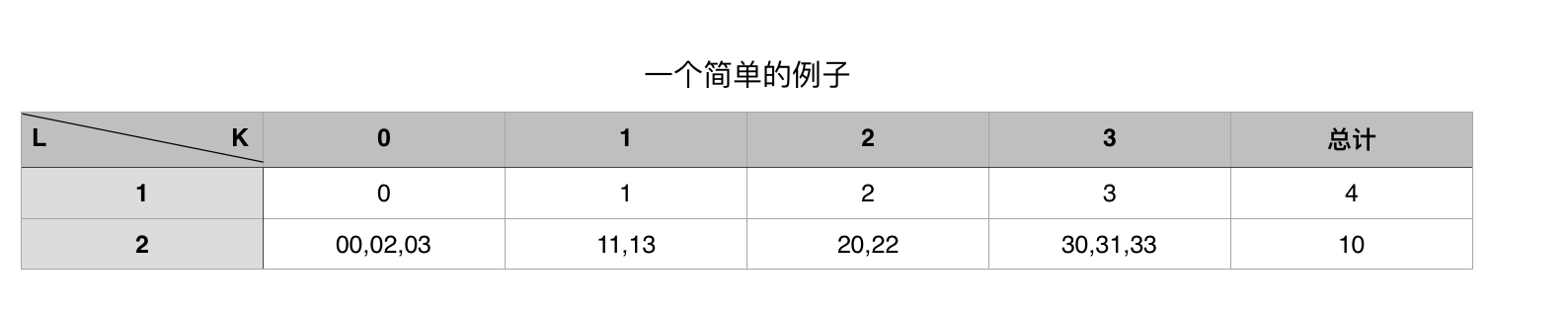
图中L为长度 K为进制数，上面的图简单说明了 4进制 如何由 L=1的K好数推导出L=2的K好数。

我想借助这个图来说明上面由**标示的语句

这道题约束条件是任意两位数字不能相临，那么，我们就让它从L=1时的K好数和L=2时首数字与L=1的那个K好数的首数字不相临，那么这个L=2的数也就是K好数。依此类推。

最后要说的就是K好数的开头不能为零。所以计算长为L，由1~N-1开头的K好数的总和，即为本题的答案。

update by 2017/4/4 20:15

by 一枝猪