[07/18NOIP模拟测试5]超级树

鬼能想到的dp定义：dp[i][j]表示在一棵i级超级树中，有j条路径同时存在且这j条路径没有公共点时，可能的情况数

刚开始我也没看懂，所以举个例子

如一个2级的超级树，父节点为1，左右儿子为2，3

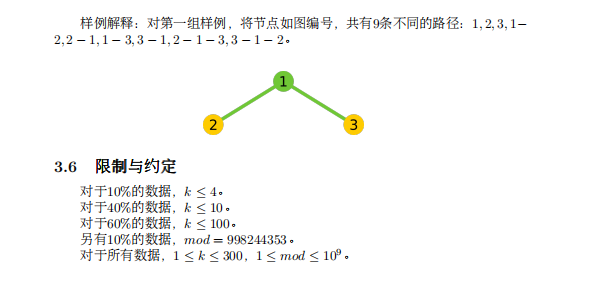
（感谢Al_Ca贡献的图，但我感觉题目里给的这个带编号更好一些。懒得把字去掉了将就着看吧）

（感谢xkl贡献的截好的图，但我斟酌了一下带上样例解释你们是不是会更好理解啊～）

（我太挑剔啦，不用给我发图啦，谢谢大家）

dp[2][1]=9,因为2级树里的路径一共有9条（样例），显然只有一条路径的话肯定没有公共点

dp[2][2]=7，(1,2)(1,3)(2,3)(2,13)(2,31)(3,12)(3,21)，注意路径方向不同就是不同的

//公告：原数有误，感谢starsing边骂我边更正

dp[2][3]=1,只有（1单独作为一条路径，2单独作为一条路径，3单独作为一条路径，共3条）这一种可能。它们没有公共点。

dp[2][4]=0,2级树只有3个点，每条路径至少1个点，所以4条路径不可能没有公共点

那么按照套路。。。递推肝它！

如果你想要得到dp[i][j]，该从什么转移过来？

情况太多了，想不出来。。。

我们尝试把dp[i][j]的情况设为已知，往后推别的

把两棵i-1级的树，配上一个根节点，合成一个i级的树，合成过程中的方案？

枚举左右子树中各有多少路径，左子树j右子树k，设sum=dp[i][j]*dp[i][k]

首先，想最简单的玩意：与根节点无关，左右子树保持原样

那么整个图中的路径数并没有变，左子树还是j个，右子树k个，只不过整个树升级了,根据乘法原理

dp[i+1][j+k]+=dp[i][j]*dp[i][k]，即dp[i+1][j+k]+=sum，就这样累加方案数就好了

下一种情况，你随便从左子树里选一条边，把这条边的终点和父节点相连，相连之后的新路径仍然与右子树当中的任何一条路径没有交点

左边的路径增长了1，但是路径的总数没有变，还是（左子树+根）有j条，右子树有k条，从左子树j个里挑出一个的方案数是j

dp[i+1][j+k]+=sum*j;　　　　----(2-1-1)

然后我们既然可以把终点延伸到父节点，我们也可以把起点延伸到父节点

我们还是从左子树中随便挑路径，把根节点连向它，同上，路径延长而总数不变

dp[i+1][j+k]+=sum*j;　　　　----(2-2-1)

你现在一直是在左子树里挑边，为什么不在右子树里也挑呢？全部同理。不过是j变成了k

dp[i+1][j+k]+=sum*k;　　　　----(2-1-2)

dp[i+1][j+k]+=sum*k;　　　　----(2-1-2)

合并2打头的这四个式子：dp[i+1][j+k]+=2*sum*(j+k);

考虑下一种情况：左子树有j条右子树有k条，可是父节点它本身还是一条啊

那么总路径数就是（左j+右k+根1）=j+k+1

dp[i+1][j+k+1]+=sum;

再下一种情况：我们从左子树中选出一条路径，把它的终点连向父节点，在从根节点连向右子树的一条路径的起点

总路径数是j+k-1，因为你把两条合成了一条

还是举例子，若左子树有三条路径ABC，右子树3条abc。合成A和根再到a，现在的路径就是A-a, B, C, b, c，为3+3-1=5条。

而选边的方法数是j*k，这个是左连根再连右。同理还有右连根再连左，所以总数*2.

dp[i+1][j+k-1]+=sum*2*j*k;

最后一种情况，也是最恶心的：左子树一条路径终点连向父节点，再由父节点连向左子树的另一条路径的起点

证明可行性：因为dp含义中已经定义，这些路径彼此没有交点，那么从中任选两条路径后，与根节点按上述方法相连后仍然这一条路径自身没有公共点，与其他边仍然没有交点，满足条件。

dp[i+1][j+k-1]+=sum*j*(j-1)　　(5-1)

因为是要在l条路径中选出两条不一样的，且与顺序有关不用除2

（你可以认为是选出的第一个路径的起点作为合成路径的起点，第二条路径的终点作为合成路径的终点，那么交换这两条路径所得到的合成路径是不同的）

同理，从右边选两条：dp[i+1][j+k-1]+=sum*k*(k-1)　　(5-2)

合并一下：dp[i][j+k-1]+=sum*(j*(j-1)+k*(k-1));

好了，没有其他情况了。5个蓝色的式子就是全部的递推式子，不重不漏。

初始状态dp[1][0]=dp[1][1]=1;

最后的答案就是dp[n][1]了，即n级树中全部的路径数，没有相交之类的限制（所以第二维选出一条路径即可）

一定一定要多取模！

完事！

但是你A不了，对不对？

主要有两种错误，稍讲一下。

TLE ：里面可能夹杂了WA，真的。

卡常，加法的取模优化，这还不够。但是有必要！

你仔细想一下枚举范围，i肯定是到n了，那么j和k呢？

能给dp[m][q]贡献答案的，是dp[m-1][?]，问号如果是大于q+1，显然就没用了。即两维之和不超过m+q

所以为了求出dp[n][1],那么两维之和就不必超过n+1。所以对j的限制就是0～（n-i+2）

那么对k的限制就更紧了，0～（n-i+2-j）

还是不够？前期的某些枚举是无效的，如k=300,你会枚举到dp[1][250]之类的

1级树里怎么可能会有250条路径嘛！

因此对枚举的上届再次限制，在满足上一个条件的前提下，还要限制j.k<=2ⁱ-1

顺便再提一下zkt的常数减半的优化：因为j和k同步的枚举，颠倒它们的顺序会累加完全一样的答案

那么就干脆把sum加倍，强制k从j+1开始枚举，特殊处理j==k即可。

WA 95了？（或者因为有T的点被显示成了WA60之类）

友情赠送测试点“1 1”

我并没有经历这个问题，因为我输出的时候顺手取模了。

不要小瞧这5分！这很关键！要长记性！

然而。。。有一个最重要问题没有解决，这个思路是怎么想到的？在题解的开头我说它很难想到。

可是“如何想到”这很关键！ 否则你只会看到别人的dp定义才会做，考试还是什么也不会。

思维这个东西很难讲清楚，但我还是要冒险说一说。[不喜勿喷]

至少，i级树从i-1级树中推来的这个分解问题这个思路应该还是能够想到的吧？

那么从这个角度出发分情况，应该是可以想到上述5种情况的。

在要用父节点拼接两条路径时，我们可以发现如果设的dp含义中如果不限制让它没有公共点，那么拼接起来无法计算！

这样也许就会可以想到了吧。。。反正我没想到。。。还要加油啊

接下来含义中已经定义了没有交点。

我们观察数据范围，应该是n³左右的，最外层枚举树的等级没什么问题，里面呢？

我们将样例输出2即245分解质因数（常用思路），发现出现了较大的质数，猜测这题不是简单粗暴的相乘，而是某些东西相乘再求和

这样我们就有了一个大体的框架（当然到这时候你还想不到限制枚举范围什么的）

 for(int i=;i<n;++I)//表示树的等级
     for(int j=;j<=n;++j)//含义未知
         for(int k=;k<=n;++k)//含义未知
             dp[i+][?]+=dp[i-][j]*dp[i-][k]*(?);

现在我们只需要猜测出那两个位置的含义是什么，式子中的问号就能凿实了。

还有什么的限制是n级别的？说实在的我的第一反应是已经用在路径中的点的数量。

但是我们可以发现每个点之间并不是平等的，它们的连边关系不同，故笼统地用它们的数量来推是不现实的。

点不行，还能是啥？只能是边了，而且没有交点。说真的，不太好想。

但是边之间的确彼此平等。。。枚举范围的确是n级别。。。

所以你就想到了。。。

好吧，我承认，有点牵强，但是的确有人能在考场上自己想出来，他们太强了，所以咱们更要练啊！

最后，给一个建议，看完了博客去打题之前，你最好再系统地理解一下，争取码代码的时候不要再回来看公式。

自己根据含义想出来，自己推式子，理解消化，做题才有意义。

记住，你不是公式的搬运工。

最后送给你们几个调试用小样例（不取模）

1 1

2 9

3 245

4 126565

5 32054326261

 #include<cstdio>
 #include<iostream>
 using namespace std;
 #define int long long
 #define sum (dp[i][l]*dp[i][r])%mod
 int dp[][],n,k,mod;
 inline void modd(long long &a){if(a>=mod)a-=mod;}
 signed main(){
     scanf("%lld%lld",&n,&mod);
     dp[][]=dp[][]=;
     for(int i=;i<n;++i) for(int l=;l<=min(n-i+,i<=?(1ll<<i)-:n-i+);++l) for(int r=;r<=min(n-i+-l,i<=?(1ll<<i)-:n-i+);++r){
         modd(dp[i+][l+r]+=sum);//直接转移
         modd(dp[i+][l+r+]+=sum);//只多了一个根自己是路径
         modd(dp[i+][l+r]+=(sum<<)*(l+r)%mod);//只把一条边伸长到根节点，双向
         modd(dp[i+][l+r-]+=l*r%mod*(sum<<)%mod);//左右通过根节点相连
         modd(dp[i+][l+r-]+=sum*(l*(l-)%mod+r*(r-)%mod)%mod);//同侧通过根节点相连
     }
     printf("%lld\n",dp[n][]%mod);
 }

考时垃圾，考后牛逼。。。有什么用