【7.10校内test】T2不等数列

【题目链接luogu】

此题在luogu上模数是2015，考试题的模数是2012。

然后这道题听说好多人是打表找规律的（就像7.9T2一样）（手动滑稽_gc）

另外手动

sy，每次测试都无意之间bibi正解，然后说自己是不会做是个什么骚气操作。

所以我们来看真.题解；

SOLUTION：

首先，输入莫得什么好说的；

当然想用快读咱也拦不住（就是想用咬我啊）；

咱可能最近因为学长讲了一道DP，印象比较深刻，所以咱居然看到这道题就想到正解应该是DP了！？

接下来就是设计DP状态了：

dp[i][j]表示i个数，恰有j个‘<’的排列方案数；

转移就很神奇很有意思了：

当我们已知dp[1~i-1][1~k]时，我们考虑求dp[i][j]；

当数从i-1~i时，显然数列增加的数是大于1~i-1的（莫得因为什么，不好解释，感性理解）；我们考虑把i这个数加在哪里：

①加在序列的最左侧：

因为i>1~i-1的任何一个数，所以一定是‘>’，因此对‘<’的多少没有影响；

②加在序列最右侧：

同理因为i>1~i-1任何一个数，所以当将i放在序列最右侧时，一定会增加一个‘<’;

③加在一个‘<’的中间：

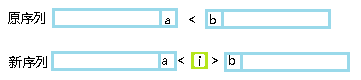
实际上不会增加‘<’，因此不会对答案产生影响qwq；

④加在一个‘>’中间：

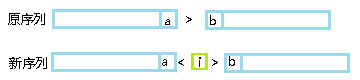
增加了一只‘<’。

所以由此我们可以推出状态转移方程：

当i加在第①③种情况时，不会产生新的‘<’，因此我们需要由dp[i-1][j]推过来。

可以计算1~i-1的序列中，共有j个‘<’号，然后还有①情况中的一种，共有j+1种情况是添加后不增加‘<’的，所以dp[i][j]+=dp[i-1][j]*(j+1);

当i加在第②④种情况时，会产生新的'<'，因此我们也需要由dp[i-1][j-1]推得：

④情况：我们知道当前情况下1~i-1中共有j-1个‘>’，总共的符号数为i-2个，因此其中‘>’数为i-2-(j-1)=i-j-1个，再加上②情况的一种，所以共有i-j个可以产生一个新的‘<’;因此dp[i][j]+=dp[i-1][j-1]*(i-j)；

转移方程：dp[i][j]=dp[i-1][j]*(j+1)+dp[i-1][j-1]*(i-j);//注意取模

然后是初始状态：

当我们有0个‘<’时，无论有几个数，这些数必须严格升序排列，也就是只有一种排列是满足有0个‘<’的；因此初始化：dp[1~n][0]=1；

最后的答案显然就是dp[n][k]了；

CODE：

#include<bits/stdc++.h>

using namespace std;

int n,k;
int dp[][];

int main(){
    scanf("%d %d",&n,&k);
    for(int i=;i<=n;i++) dp[i][]=;
    for(int i=;i<=n;i++){
        for(int j=;j<=k;j++){
            dp[i][j]=(dp[i-][j]*(j+)%2015+dp[i-][j-]*(i-j)%2015)%2015;
        }
    }
    printf("%d",dp[n][k]);
    return ;
}

end-