梯度vs Jacobian矩阵vs Hessian矩阵

梯度向量

定义：

目标函数f为单变量，是关于自变量向量x=(x1,x2,…,xn)T的函数，

单变量函数f对向量x求梯度，结果为一个与向量x同维度的向量，称之为梯度向量；

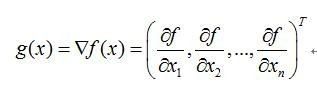
1. Jacobian

在向量分析中, 雅可比矩阵是一阶偏导数以一定方式排列成的矩阵, 其行列式称为雅可比行列式. 还有, 在代数几何中, 代数曲线的雅可比量表示雅可比簇：伴随该曲线的一个代数群, 曲线可以嵌入其中.

雅可比矩阵

定义：

目标函数f为一个函数向量，f=(f1(x),f2(x),…fm(x))T;其中，自变量x=(x1,x2,…,xn)T；函数向量f对x求梯度，结果为一个矩阵；行数为f的维数；列数位x的维度，称之为Jacobian矩阵；其每一行都是由相应函数的梯度向量转置构成的；

雅可比矩阵的重要性在于它体现了一个可微方程与给出点的最优线性逼近. 因此, 雅可比矩阵类似于多元函数的导数.

【注】：梯度向量Jacobian矩阵的一个特例；

当目标函数为标量函数时，Jacobian矩阵是梯度向量；

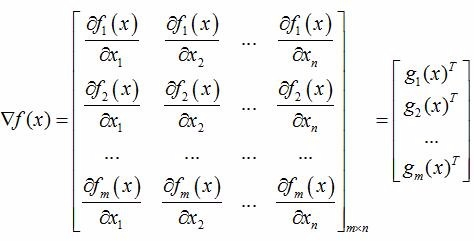
2. 海森Hessian矩阵

在数学中, 海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数如下：

(也有人把海森定义为以上矩阵的行列式)海森矩阵被应用于牛顿法解决的大规模优化问题.

实际上，Hessian矩阵是梯度向量g(x)对自变量x的Jacobian矩阵：

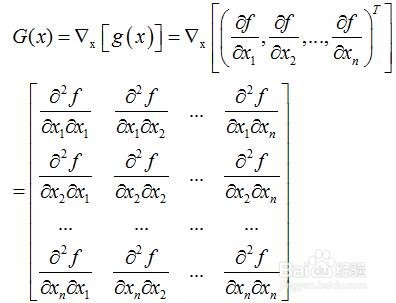
海森矩阵在牛顿法中的应用

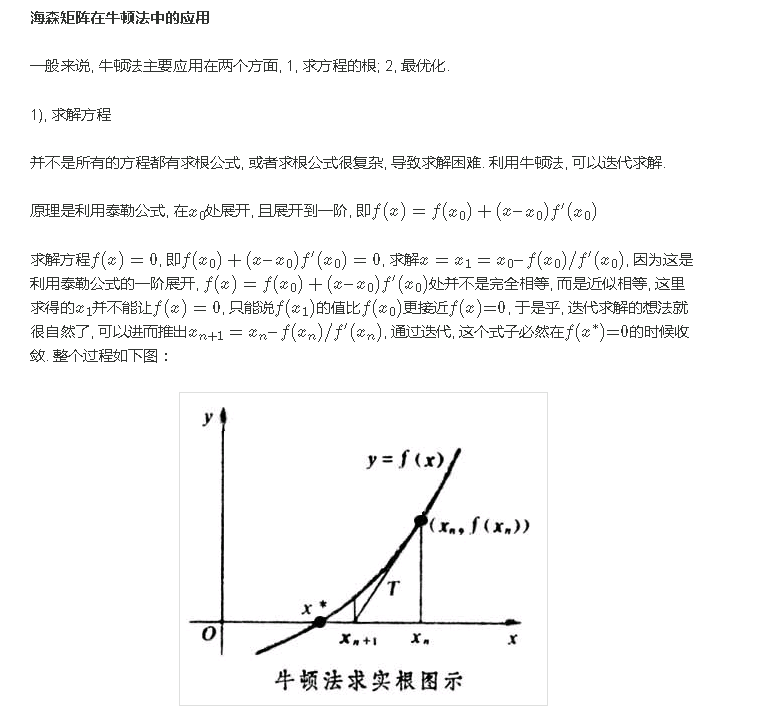
2), 最优化

在上面讨论的是2维情况, 高维情况的牛顿迭代公式是：

参考：https://www.cnblogs.com/ChenKe-cheng

文献： 牛顿法和Hessian矩阵