Hdoj 2454.Degree Sequence of Graph G 题解

Problem Description

Wang Haiyang is a strong and optimistic Chinese youngster. Although born and brought up in the northern inland city Harbin, he has deep love and yearns for the boundless oceans. After graduation, he came to a coastal city and got a job in a marine transportation company. There, he held a position as a navigator in a freighter and began his new life.

The cargo vessel, Wang Haiyang worked on, sails among 6 ports between which exist 9 routes. At the first sight of his navigation chart, the 6 ports and 9 routes on it reminded him of Graph Theory that he studied in class at university. In the way that Leonhard Euler solved The Seven Bridges of Knoigsberg, Wang Haiyang regarded the navigation chart as a graph of Graph Theory. He considered the 6 ports as 6 nodes and 9 routes as 9 edges of the graph. The graph is illustrated as below.



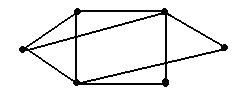
According to Graph Theory, the number of edges related to a node is defined as Degree number of this node.

Wang Haiyang looked at the graph and thought, If arranged, the Degree numbers of all nodes of graph G can form such a sequence: 4, 4, 3,3,2,2, which is called the degree sequence of the graph. Of course, the degree sequence of any simple graph (according to Graph Theory, a graph without any parallel edge or ring is a simple graph) is a non-negative integer sequence?

Wang Haiyang is a thoughtful person and tends to think deeply over any scientific problem that grabs his interest. So as usual, he also gave this problem further thought, As we know, any a simple graph always corresponds with a non-negative integer sequence. But whether a non-negative integer sequence always corresponds with the degree sequence of a simple graph? That is, if given a non-negative integer sequence, are we sure that we can draw a simple graph according to it.?

Let's put forward such a definition: provided that a non-negative integer sequence is the degree sequence of a graph without any parallel edge or ring, that is, a simple graph, the sequence is draw-possible, otherwise, non-draw-possible. Now the problem faced with Wang Haiyang is how to test whether a non-negative integer sequence is draw-possible or not. Since Wang Haiyang hasn't studied Algorithm Design course, it is difficult for him to solve such a problem. Can you help him?

Input

The first line of input contains an integer T, indicates the number of test cases. In each case, there are n+1 numbers; first is an integer n (n<1000), which indicates there are n integers in the sequence; then follow n integers, which indicate the numbers of the degree sequence.

Output

For each case, the answer should be "yes"or "no" indicating this case is "draw-possible" or "non-draw-possible"

Sample Input

2
6 4 4 3 3 2 2
4 2 1 1 1

Sample Output

yes
no

Source

2008 Asia Regional Harbin

---

思路

根据Havel-Hakimi定理 ：

• 非递增排序当前数列\(d[n]\)
• 让\(k=d[1]\)，将k从数组中移除
• 从第2个开始的前K个元素都-1
• 不断重复上述过程直到序列出现负数=不可图，全都为0=可图

详细见代码注释

代码

#include<bits/stdc++.h>
using namespace std;
int a[1001];
int main()
{
	int t;
	cin >> t;
	while(t--)
	{
		int n;
		cin >> n;
		for(int i=1;i<=n;i++)
			cin >> a[i];
		sort(a+1,a+n+1,[](int x,int y)->bool{ return x>y;});
		bool flag = false;
		while(true)
		{
			int k = a[1];
			if(k < 0 || a[n] < 0)//如果之前出现了负数那么排序后最后一个肯定小于0不符合
			{
				flag = false;
				break;
			}else
			if(k==0)
			{
				flag = true;
				break;
			}else
			{
				for(int i=2;k>0;i++)//从第2个起接下来k个元素都-1
				{
					a[i]--;
					if(a[i] < 0)
					{
						flag = false;
						break;
					}
					k--;
				}
				a[1] = 0;
				sort(a+1,a+n+1,[](int x,int y)->bool{ return x>y;});
			}
			if(flag) break;
		}
		if(flag)
			cout << "yes" << endl;
		else
			cout << "no" << endl;
	}
	return 0;
}