02(e)多元无约束优化问题- 梯度的两种求解方法以及有约束转化为无约束问题

2.1 求解梯度的两种方法

以$f(x,y)={{x}^{2}}+{{y}^{3}}$为例，很容易得到：

$\nabla f=\left[ \begin{aligned}& \frac{\partial f}{\partial x} \\& \frac{\partial f}{\partial y} \\\end{aligned} \right]=\left[ \begin{aligned}& 2x \\& 3{{y}^{2}} \\\end{aligned} \right]$

这样就很容易求得某一点的梯度。

但是如果梯度的表达式很难写出来，或者根本就写不出来的时候，尤其定义去求梯度可是可以的：

$\nabla f=\left[ \begin{aligned}& \frac{\partial f}{\partial x} \\& \frac{\partial f}{\partial y} \\\end{aligned} \right]=\left[ \begin{aligned}& \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x} \\& \frac{f(x,y+\Delta y)-f(x,y)}{\Delta y} \\\end{aligned} \right]$

在实际算的过程中这里的$\Delta x$，$\Delta y$也不用取太小一般$1\times {{10}^{-7}}$左右就可以了。

2.2 某些有约束优化问题可以转化为无约束优化问题：

\[\begin{aligned}& \operatorname{minimize}\text{  }f({{x}_{1}},{{x}_{2}})\text{         }\operatorname{minimize}\text{  }f({{x}_{1}},{{x}_{2}}) \\& \text{               }{{x}_{1}}>0\text{      }\Rightarrow \text{                   }{{x}_{1}}={{{\hat{x}}}^{2}}_{1} \\& \text{               }{{x}_{2}}\le -30\text{                         }-\text{30}-{{x}_{2}}\text{=}{{{\hat{x}}}^{2}}_{2}\text{ }\Rightarrow -\text{30}-{{{\hat{x}}}^{2}}_{2}\text{=}{{x}_{2}} \\\end{aligned}\]

把上式中左边的不等式优化，转化为右边的等式优化，再把等式代入目标函数中，形成了式(24)这样的无约束优化问题：

\[\operatorname{minimize}\text{  }f({{\hat{x}}_{1}},{{\hat{x}}_{2}})\]

通过优化求解得到满足上式的次优解$\left( {{{{\hat{x}}'}}_{1}},{{{{\hat{x}}'}}_{2}} \right)$，则原优化问题的解可以写为：

\[\begin{aligned}& \text{ }{{x}_{1}}={{\left( {{{{\hat{x}}'}}_{\text{1}}} \right)}^{\text{2}}} \\& {{x}_{2}}\text{=}-\text{30}-{{\left( {{{{\hat{x}}'}}_{2}} \right)}^{\text{2}}} \\\end{aligned}\]

这样的做法会增加目标函数的非线性度，但是很好的把有约束问题转变为无约束问题。下面这个带约束的优化问题同样可以用上述方式处理：

\[\begin{aligned}& \operatorname{minimize}\text{  }f({{x}_{1}},{{x}_{2}})\text{         }\operatorname{minimize}\text{  }f({{x}_{1}},{{x}_{2}}) \\ & \text{               3}\le {{x}_{1}}\le 12\text{      }\Rightarrow \text{                   } \\\end{aligned}\]

这里的转化，我想着用Sigmoid函数(logistic函数)：

$f\left( x \right)=\frac{1}{1+{{e}^{-x}}}$

它的图像如下：

这样就可以用下面这个式子代替上述对${{x}_{1}}$的约束：

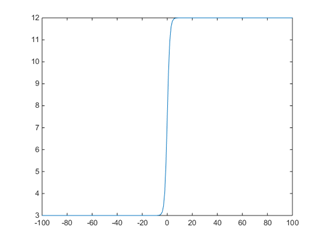
${{x}_{1}}=\frac{9}{1+{{e}^{-\hat{x}}}}+3$

它的图像如下