数构与算法 | 什么是大 O 表示算法时间复杂度

　正文:

开篇我们先思考这么一个问题：一台老式的 CPU 的计算机运行 O(n) 的程序，和一台速度提高的新式 CPU 的计算机运 O(n2) 的程序。谁的程运行效率高呢？

答案是前者优于后者。为什么呢？我们从时间复杂度分析就可以知道。

1、什么是时间复杂度？

在进行算法分析时，语句总的执行次数 T(n) 是关于问题的规模n 的函数，进而分析 T(n) 随 n 的变化情况并确定 T(n) 的数量级，算法的时间复杂度，也就是算法的时间度量，记作：T(n) = O(f( ))。它表示随问题的规模 n 的增大，算法的执行时间的增长率 f(n) 的增长率相同，称作算法的渐近时间复杂度，简称为时间的复杂度，其中 f(n) 是问题规模n的某个函数。

这样用大写 [ O( ) ] 来体现算法时间复杂度的记法，我们就称之为大O记法。例如：O(n)、O(1)、O(n2)、O(log n) 等等。一般情况下，随着 n 的增大，T(n) 增长最慢的算法为最优算法。

2、推导大O阶的方法

如何推导大O阶的表示方法，总结了三句口诀：

1. 用时间1取代运算时间中的所有加法常数。
2. 在修改后的运行的函数中，只保留最高阶项。
3. 如果最高阶项存在且不是1，则去除与这个项相乘的常数。得到的结果就是大O阶。

说了太多文字显得太抽象，我们来看看一个例子你就明白了。

如图这个时间复杂度你知道是多少吗？

​

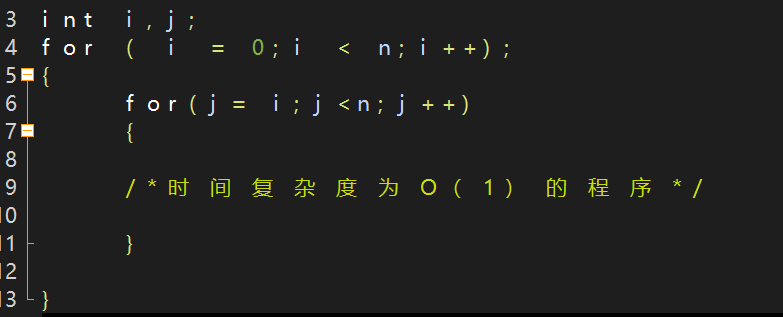
分析：

当 i = 0时，内循环执行了 n 次，

当 i = 1时，内循环执行了 n-1 次，

····

当 i = n-1时。执行了 1 次，所以总的执行次数为：n = (n-1)+(n-2)+ ··· + 1= n(n+1)/2 = n2/2+n/2。

由上面的公式可得：第一条代码中没有加法常数项，不考虑；第二条只保留最高阶项，因此保留 n2/2；第三条去除这个项相乘的常数，所以去除了 1/2；最终我们得到的代码段时间复杂度就是 O(n2)。

所以有了上面这个公式我们就可以对一般的时间复杂度大O的推导求解，其实理解大 O 推导不算难，难得是对数列的一些相关运算。更多的是考察你的数学功底。所以能不能写出好的高效率代码和你的数学功底有关哦。数学真的很重要（认真脸）。

3、一些常用的O( )时间复杂度推导

例1：O(1)常数阶

int sum = 0, n = 100;    /* 执行一次 */

sum = (1+n) *n/2;        /* 执行一次 */

printf("the sum is：%d",sum)；   /* 执行一次 */

我们可以看出运行次数的函数是 f(n) = 3。根据我们上面的大O阶公式 1 可以得到，把常数项 3 改为 1，在保留最高阶时发现没有最高阶项，所以时间复杂度为大 O(1)。也就是说，无论算法是 3 次还是 30 次，哪怕是 300 次，这些只要是常数项，它的时间复杂度都为大 O(1)，而不是O(3)、O(30)、O(300)。即我们称之为常数阶。

例2：O(n)线性阶

​

从上面的这段代码我们可以看出，它的时间复杂度为O(n)，因为循环体中的代码需要执行n次。

例3：O(log n)对数阶

​

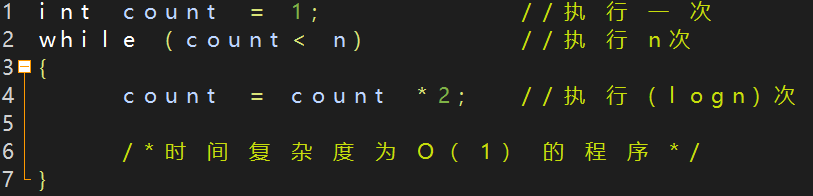
上面代码我们可以看出，count = count * 2 之后就距离 n 更近里布，也就是说，有多少个 2 相乘后大于 n,就退出循环。所以我们可以由 2x = n 推导出 x = log2n ,像这样的循环时间复杂度，我们就称为对数阶的复杂度即为 O(log n)。

例4：O(n2)平方阶

​

这是有 2 个 for 语句组成的循环，是每一个循环代码执行 n次，所以整个代码就是 n*n 次，所以时间复杂度为 O(n2) 。

注意：如果外面的的循环次数不是 n 而是 m 那么时间复杂度就变为了 O(m*n) ,所以，循环的时间复杂度就等于循环体的的复杂度乘上该循环的运行次数。

数据结构中我们一般常用的时间复杂度表示有：O(1)、O(n)、O(n2)、O(log n)、O(nlog n)、O(n3)、O(2n)。

按时间复杂度所耗费的时间从大到小排序依次为：

O(1) < O(log n) < O(n) < O(nlog n) < O(n2) < O(n3) < O(2n)

到这里，我们就可以清楚的明白了开篇的问题，为什么老式 CPU 程序运行速率比新式的 CPU 运行效率高的原因就是应为O(n)< O(n2) 时间复杂度的关系，所以能写出好的算法是可以让计算机变得轻松的。

4、时间复杂度的三种情况

1.最好情况时间复杂度：

顾名思义，看名字你就知道，就是代码执行的次数为一次即为最好的 O(1)。这是要我们写代码最想要的。但是这是不现实的。

2.最坏情况时间复杂度：

同样的看名字你也可以知道，这是代码执行的总次数很多，每次都要运行 n 次，所以表示为 O(n)。这是我们写代码最不想要的。当然这也是不现实的。

3.平均时间复杂度：

就是把最好情况时间复杂度和最坏情况时间复杂度求取一平均值，这是我们写代码最有意义的，因为这是期望的运行时间，所以在写代码时应当考虑这一点。

5、算法空间复杂度

所谓算法的空间复杂度就是通过计算机算法所需求的存在空间实现。计算公式可以表示为：S(n) = O( f(n) )，其中，n为问题的规模，f(n) 为语句关于 n 所占存储空间的函数。

一般情况下，一个程序在机器上运行时，除了考虑到程序的本身运行指令，常数，变量和输入数据外，还需要考虑存储对数据操作的存储单元。

我们在写代码时完全可以用空间换取时间，两者不存在绝对的好与坏，这么用好二者关系取决于你用在什么地方。所以，实际情况还是要根据工程代码做最完美的选择。

6、总结

1. 时间复杂度大O表示方法的由来。
2. 大O推导的表示方法和常用的大O表示法时间复杂度。
3. 时间复杂度的三种情况：最好情况、最坏情况和平均情况。
4. 算法空间复杂度，适当情况可以用空间换取时间。

=====================（完）===================

​