Sparse Principal Component Analysis via Rotation and Truncation

对以往一些SPCA算法复杂度的总结
Notation
论文概述
原始问题
问题的变种
算法
- 固定$X$,计算$R$
- 固定$R$，求解$X$ （$Z =VR^{\mathrm{T}}$）
  - 1-范数
$T-\ell_0$（新的初始问题）
T-sp 考虑稀疏度的初始问题
T-en 考虑Energy的问题
代码

SPCArt算法，利用旋转（正交变换更为恰当，因为没有体现出旋转这个过程），交替迭代求解sparse PCA。

对以往一些SPCA算法复杂度的总结

注：$r$是选取的主成分数目，$m$为迭代次数,$p$为样本维度，$n$为样本数目。本文算法，需要先进行SVD，并未在上表中给出。

Notation

论文概述

$A = U\Sigma V^{\mathrm{T}}$

$V_{1:r}=[V_1,V_2,\ldots, V_r] \in \mathbb{R}^{p\times r}$就是普通PCA的前$r$个载荷向量（loadings,按照特征值降序排列）

$\forall 旋转矩阵（正交矩阵）R \in \mathbb{R}^{r \times r}$

$V_{1:r}R$也是彼此正交的，张成同一子空间的向量组。

原始问题

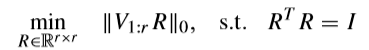
如果能解出来，当然好，可是这是一个很难求解的问题，所以需要改进。

问题的变种

$V_{1:r}$直接用$V$表示了，为了符号的简洁。

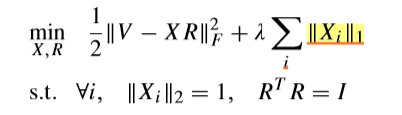
变成这个问题之后，我们所追求的便是$X$了，$X_i$，就是我们要的载荷向量，显然，这个问题所传达出来的含义是：

1.我们希望$XR$与$V$相差不大，意味着$X_i$近似正交且张成同一个子空间。

2.$\|X_i\|_1$作为惩罚项，可以起到稀疏化的作用（这是1-范数的特点）。

算法

这是一个交替迭代算法，我们来分别讨论。

固定$X$,计算$R$

当固定$X$,之后，问题就退化为：

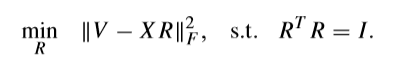
这个问题在Sparse Principal Component Analysis（Zou 06）这篇论文里面也有提到。

上述最小化问题，可以变换为

$max \quad tr(V^{\mathrm{T}}XR), \quad s.t. \quad R^{\mathrm{T}}R=I$

若$X^{\mathrm{T}}V=WDQ^{\mathrm{T}}$

就是要最大化：

$tr(QDW^{\mathrm{T}}R)=tr(DW^{\mathrm{T}}RQ)\leq tr(D)$

当$R = WQ^{\mathrm{T}}$(注意$W^{\mathrm{T}}RQ$是正交矩阵)。

固定$R$，求解$X$ （$Z =VR^{\mathrm{T}}$）

1-范数

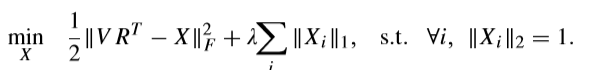
注意：$\|VR^{\mathrm{T}}-X\|_F^2=\|(V-XR)R^{\mathrm{T}}\|_F^2$，所以这个问题和原始问题是等价的。

经过转换，上述问题还等价于：

$max_{X_i} \quad Z_i^{\mathrm{T}}X_i-\lambda\|X_i\|_1 \quad i=1,2,\ldots,r$

通过分析（蛮简单的，但是不好表述），可以得到：

$X_i^*=S_\lambda(Z_i)/\|S_\lambda(Z_i)\|_2$

$T-\ell_0$（新的初始问题）

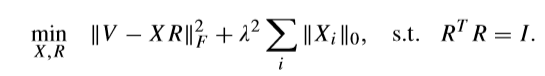
$R$的求解问题没有变化，考虑$R$固定的时候，求解$X$。

等价于：

$\mathop{min}\limits_{X_{ij},Z_{ij}} \quad (Z_{ij}-X_{ij})^2+\lambda^2\|X_{ij}\|_0$

显然，若$X_{ij}^* \neq 0$,$X_{ij}^*=Z_{ij}$，此时函数值为$\lambda^2$

若$X_{ij}^* = 0$,值为$Z_{ij}^2$，所以，为了最小化值，取：

$min \{Z_{ij}^2,\lambda^2\}$,也就是说，

$X_{ij}=0 \quad if\:Z_{ij}^2>\lambda^2$ 否则， $X_{ij}=Z_{ij}$

$X_i^*=H_\lambda(Z_i)/\|H_\lambda(Z_i)\|_2$

T-sp 考虑稀疏度的初始问题

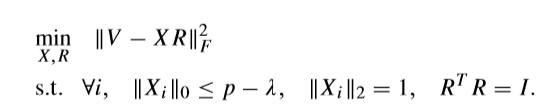
$\lambda \in \{0, 1, 2,\ldots,p-1\}$

$R$的求法如出一辙，依旧只需考虑在$R$固定的情况下，如何求解$X$的情况。

等价于：

$max \quad Z_i^{\mathrm{T}}X_i$ 在条件不变的情况下。

证明挺简单的，但不好表述，就此别过吧。

最优解是：$X_i^*=P_\lambda(Z_i)/\|P_\lambda(Z_i)\|_2$

T-en 考虑Energy的问题

$X_i = E_\lambda(Z_i)/\|E_\lambda(Z_i)\|_2$

文章到此并没有结束，还提及了一些衡量算法优劣的指标，但是这里就不提了。大体的思想就在上面，我认为这篇论文好在，能够把各种截断方法和实际优化问题结合在一起，很不错。

代码

def Compute_R(X, V):

    W, D, Q_T = np.linalg.svd(X.T @ V)

    return W @ Q_T

def T_S(V, R, k): #k in [0,1)

    Z = V @ R.T

    sign = np.where(Z < 0, -1, 1)

    truncate = np.where(np.abs(Z) - k < 0, 0, np.abs(Z) - k)

    X = sign * truncate

    X = X / np.sqrt((np.sum(X ** 2, 0)))

    return X

def T_H(V, R, k): #k in [0,1)  没有测试过这个函数

    Z = V @ R.T

    X = np.where(np.abs(Z) > k, Z, 0)

    X = X / np.sqrt((np.sum(X ** 2, 0)))

    return X

def T_P(V, R, k): #k belongs to {0, 1, 2, ..., (p-1)}    没有测试过这个函数

    Z = V @ R.T

    Z[np.argsort(np.abs(Z), 0)[:k], np.arange(Z.shape[1])] = 0

    X = Z / np.sqrt((np.sum(Z ** 2, 0)))

    return X

def Main(C, r, Max_iter, k):  #用T_S截断  可以用F范数判断是否收敛，为了简单直接限定次数

    value, V_T = np.linalg.eig(C)

    V = V_T[:r].T

    R = np.eye(r)

    while Max_iter > 0:

        Max_iter -= 1

        X = T_S(V, R, k)

        R = Compute_R(X, V)

    return X.T

结果，稀疏的程度大点，反而效果还好点。