POJ 2446 最小点覆盖

Chessboard

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 14787		Accepted: 4607

Description

Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below). 

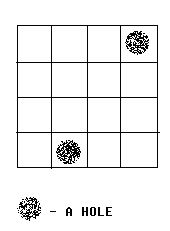
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below: 
1. Any normal grid should be covered with exactly one card. 
2. One card should cover exactly 2 normal adjacent grids.

Some examples are given in the figures below: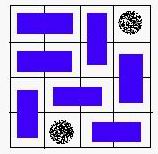 
 
A VALID solution.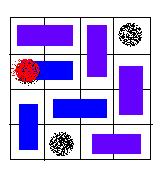
 
An invalid solution, because the hole of red color is covered with a card.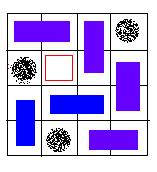
 
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

Input

There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.

Output

If the board can be covered, output "YES". Otherwise, output "NO".

Sample Input

4 3 2
2 1
3 3

Sample Output

YES

Hint

 
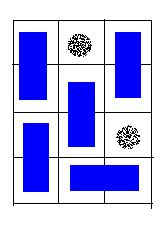
A possible solution for the sample input.

Source

POJ Monthly,charlescpp

 

 

题目意思：

一个n*m的棋盘，现用1*2的木板覆盖棋盘，其中有黑色圆的棋盘单位不能被覆盖。问能否把棋盘中可以覆盖的单位全部覆盖（不能重复覆盖）。

 

思路：

相邻棋盘单位奇偶性不同建图，判断最大匹配*2是否等于可以覆盖点数即可。

 

 

代码：

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <iostream>
 #include <vector>
 #include <queue>
 #include <cmath>
 #include <set>
 using namespace std;
 
 #define N 35
 
 int max(int x,int y){return x>y?x:y;}
 int min(int x,int y){return x<y?x:y;}
 int abs(int x,int y){return x<?-x:x;}
 
 int n, m;
 vector<int>ve[N*N];
 int from[N*N];
 bool visited[N*N];
 
 int march(int u){
     int i, v;
     for(i=;i<ve[u].size();i++){
         v=ve[u][i];
         if(!visited[v]){
             visited[v]=true;
             if(from[v]==-||march(from[v])){
                 from[v]=u;
                 return ;
             }
         }
     }
     return ;
 }
 int map[N][N];
 main()
 {
     int i, j, k;
 
     int x, y;
     while(scanf("%d %d %d",&n,&m,&k)==){
         memset(map,-,sizeof(map));
         int maxh=;
         for(i=;i<n;i++){
             for(j=;j<m;j++){
                 if(j==){
                     if(i==) map[i][j]=;
                     else {
                         if(m&) map[i][j]=map[i-][m-]+;
                         else map[i][j]=map[i-][m-]+;
                     }
                 }
                 else map[i][j]=map[i][j-]+;
                 maxh=max(maxh,map[i][j]);
             //    printf("%d ",map[i][j]);
             }
             //cout<<endl;
         }
         for(i=;i<k;i++){
             scanf("%d %d",&x,&y);
             map[y-][x-]=-;
         }
         int nn=;
         for(i=;i<n;i++){
             for(j=;j<m;j++){
                 if(map[i][j]==-) nn++;
             }
         }
 
         for(i=;i<=maxh;i++) ve[i].clear();
         for(i=;i<n;i++){
             for(j=;j<m;j++){
                 if(map[i][j]!=-&&(map[i][j]&)){
                     if(i>&&map[i-][j]!=-) ve[map[i][j]].push_back(map[i-][j]);
                     if(i<n-&&map[i+][j]!=-) ve[map[i][j]].push_back(map[i+][j]);
                     if(j>&&map[i][j-]!=-) ve[map[i][j]].push_back(map[i][j-]);
                     if(j<m-&&map[i][j+]!=-) ve[map[i][j]].push_back(map[i][j+]);
                 }
             }
         }
         int num=;
         memset(from,-,sizeof(from));
         for(i=;i<=maxh;i++){
             memset(visited,false,sizeof(visited));
             if((i&)&&march(i)) num++;
         }
         if(num*==n*m-nn) printf("YES\n");
         else printf("NO\n");
     }
 }