Tourists Gym - 101002I LCA——dfs+RMQ在线算法

　　LCA（Least Common Ancestors），即最近公共祖先，是指这样一个问题：在有根树中，找出某两个结点u和v最近的公共祖先（另一种说法，离树根最远的公共祖先）。

　　知识需求：1）RMQ的ST算法   2）欧拉序列

1）RMQ的ST算法：

　　可以参考我的这篇博客：RMQ原理及实现

2）欧拉序列：

　　所谓欧拉序，就是从根结点出发，按dfs的顺序经过每一个结点最后绕回原点的顺序，比如下面这个例子，欧拉序就是A-B-D-B-E-G-E-B-A-C-F-H-F-C-A

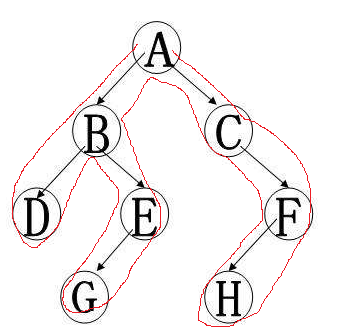
　　那么欧拉序和rmq与LCA有什么关系呢，首先我们知道RMQ可以方便的在线求出区间最小值，以求上图中DG两点最近公共祖先为例，我们先处理出他的欧拉序，我们记录下每个结点第一次被访问的时间，以及每个时间访问的结点编号与结点深度，这时，我们不难发现，D与G第一次出现的时间之间的区域深度最小值就是这两个点对应的最近公共祖先B的深度，我们修改rmq，让其不再返回最小深度，而是返回区间最小深度对应的下标，这里就是求欧拉序中的访问时间，有了这个时间，加上之前的记录，我们可以直接得出该点的编号，从而求出最近公共祖先。

练习题：题目链接

练习题AC代码：

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 #include <vector>
 #include <set>
 #include <queue>
 #include <map>

 using namespace std;

 const int MAXN =  * ;

 int rmq[MAXN * ];    //节点深度序列

 struct ST {
     int mm[MAXN * ];
     int dp[MAXN][];
     void init(int n) {
         mm[] = -;
         for(int i = ; i <= n; ++i) {
             mm[i] = ((i & (i - )) == ) ? mm[i - ] +  : mm[i - ];
             dp[i][] = i;
         }
         for(int j = ; j <= mm[n]; ++j)
             for(int i = ; i + ( << j) -  <= n; ++i)
                 dp[i][j] = rmq[dp[i][j - ]] < rmq[dp[i + ( << (j - ))][j - ]] ? dp[i][j - ] : dp[i + ( << (j - ))][j - ];
     }

     int query(int a, int b) {
         if(a > b) swap(a, b);
         int k = mm[b - a + ];
         return rmq[dp[a][k]] <= rmq[dp[b - ( << k) + ][k]] ? dp[a][k] : dp[b - ( << k) + ][k];
     }
 };

 struct Edge{
     int to, next;
 };

 Edge edge[MAXN * ];
 int tot, head[MAXN];

 int F[MAXN * ];
 int P[MAXN];
 int cnt;
 ST st;

 void init() {
     tot = ;
     memset(head, -, sizeof(head));
 }

 void addedge(int u, int v) {
     edge[tot].to = v;
     edge[tot].next = head[u];
     head[u] = tot++;
 }

 int d[MAXN];

 void dfs(int u, int pre, int dep) {
     d[u] = dep;
     F[++cnt] = u;
     rmq[cnt] = dep;
     P[u] = cnt;
     for(int i = head[u]; i != -; i = edge[i].next) {
         int v = edge[i].to;
         if(v == pre) continue;
         dfs(v, u, dep + );
         F[++cnt] = u;
         rmq[cnt] = dep;
     }
 }

 void LCA_init(int root, int node_num) {
     cnt = ;
     dfs(root, root, );
     st.init( * node_num - );
 }

 int query_lca(int u, int v) {
     return F[st.query(P[u], P[v])];
 }

 int main()
 {
     int T, N, u, v;
     scanf("%d", &N);
     init();
     for(int i = ; i < N; ++i) {
         scanf("%d%d", &u, &v);
         addedge(u, v);
         addedge(v, u);
     }
     LCA_init(, N);

     long long ans = ;
     for(int i = ; i + i <= N; ++i) {
         for(int j = i + i; j <= N; j += i) {
             ans += d[i] + d[j] +  -  * d[query_lca(i, j)];
         }
     }
     printf("%lld\n", ans);

     return ;
 }