(转)行为树（Behavior Tree）实践（1）– 基本概念

通过一个例子来介绍一下行为树的基本概念，会比较容易理解，看下图：

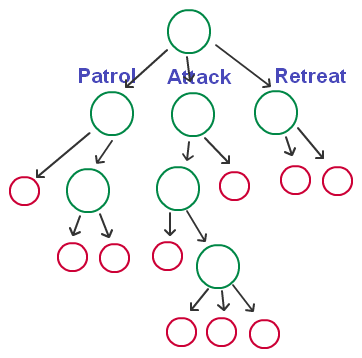
这是我们为一个士兵定义的一颗行为树（可以先不管这些绿圈和红圈是干吗的），首先，可以看到这是一个树形结构的图，有根节点，有分支，而且子节点个数可以任意，然后有三个分支，分别是巡逻（Patrol），攻击（Attack），逃跑（Retreat），这个三个分支可以看成是我们为这个士兵定义的三个大的行为（Behavior），当然，如果有更多的行为，我们可以继续在根节点中添加新的分支。当我们要决策当前这个士兵要做什么样的行为的时候，我们就会自顶向下的，通过一些条件来搜索这颗树，最终确定需要做的行为（叶节点），并且执行它，这就是行为树的基本原理。

值得注意的是，我们标识的三大行为其实并不是真正的决策的结果，它只是一个类型，来帮助我们了解这个分支的一些行为是属于这类的，真正的行为树的行为都是在叶节点上，一般称之为行为节点（Action Node），如下图红圈表示的

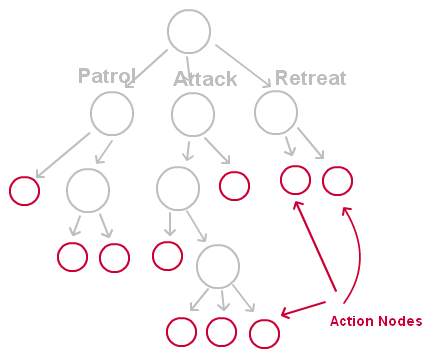
这些叶节点才是我们真正通过行为树决策出来的结果，如果用我以前提到的那个层次化的AI结构来描述的话，这些行为结果，相当于就是一个个定义好的“请求”（Request），比如移动（Move），无所事事（Idle），射击（Shoot）等等。所以行为树是一种决策树，来帮助我们搜寻到我们想要的某个行为。

行为节点是游戏相关的，因不同的游戏，我们需要定义不同的行为节点，但对于某个游戏来说，在行为树上行为节点是可以复用的，比如移动，在巡逻的分支上，需要用到，在逃跑分支上，也会用到，这种情况下，我们就可以复用这个节点。行为节点一般分为两种运行状态：

1. 运行中（Executing）：该行为还在处理中
2. 完成（Completed）：该行为处理完成，成功或者失败

除了行为节点，其余一般称之为控制节点（Control Node），用树的“学名”的话，就是那些父节点，如下图绿圈表示

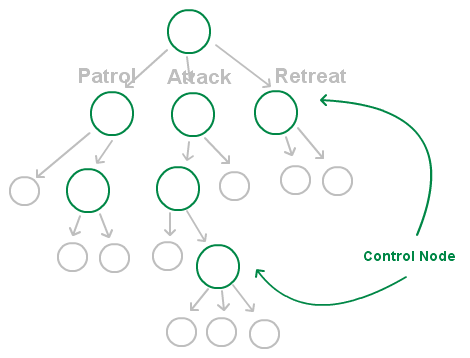
控制节点其实是行为树的精髓所在，我们要搜索一个行为，如何搜索？其实就是通过这些控制节点来定义的，从控制节点上，我们就可以看出整个行为树的逻辑走向，所以，行为树的特点之一就是其逻辑的可见性。

我们可以为行为树定义各种各样的控制节点（这也是行为树有意思的地方之一），一般来说，常用的控制节点有以下三种

1. 选择（Selector）：选择其子节点的某一个执行
2. 序列（Sequence）：将其所有子节点依次执行，也就是说当前一个返回“完成”状态后，再运行先一个子节点
3. 并行（Parallel）：将其所有子节点都运行一遍

用图来表示的话，就是这样，依次为选择，序列和并行

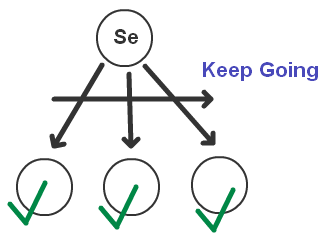
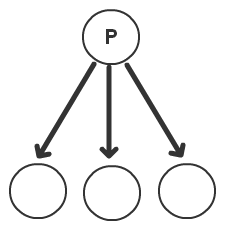
可以看到，控制节点其实就是“控制”其子节点（子节点可以是叶节点，也可以是控制节点，所谓“执行控制节点”，就是执行其定义的控制逻辑）如何被执行，所以，我们可以扩展出很多其他的控制节点，比如循环（Loop）等，与行为节点不同的是，控制节点是与游戏无关的，因为他只负责行为树逻辑的控制，而不牵涉到任何的游戏代码。如果是作为一个行为树的库的话，其中就一定会包含定义好的控制节点库。

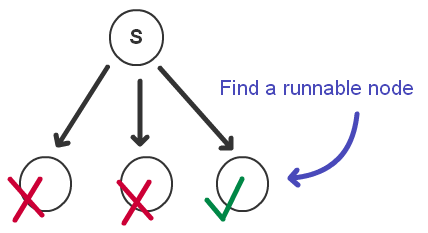
如果我们继续考察选择节点，会产生一个问题，如何从子节点中选择呢？选择的依据是什么呢？这里就要引入另一个概念，一般称之为前提（Precondition），每一个节点，不管是行为节点还是控制节点，都会包含一个前提的部分，如下图

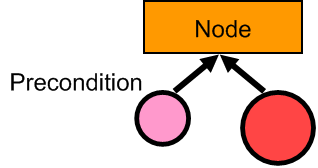
前提就提供了“选择”的依据，它包含了进入，或者说选择这个节点的条件，当我们用到选择节点的时候，它就是去依次测试每一个子节点的前提，如果满足，则选择此节点。由于我们最终返回的是某个行为节点（叶节点），所以，当前行为的“总”前提就可以看成是：

当前行为节点的前提 And 父节点的前提 And 父节点的父节点的前提 And….And 根节点的前提（一般是不设，直接返回True）

行为树就是通过行为节点，控制节点，以及每个节点上的前提，把整个AI的决策逻辑描述了出来，对于每次的Tick，可以用如下的流程来描述：

action = root.FindNextAction(input);
if action is not empty then
action.Execute(request,  input)  //request是输出的请求
else
print “no action is available”

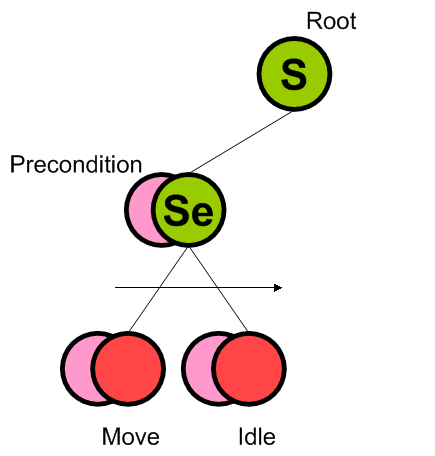
从概念上来说，行为树还是比较简单的，但对AI程序员来说，却是充满了吸引力，它的一些特性，比如可视化的决策逻辑，可复用的控制节点，逻辑和实现的低耦合等，较之传统的状态机，都是可以大大帮助我们迅速而便捷的组织我们的行为决策。希望这次简单的介绍，对大家有所帮助，能力有限，不一定能表述的很清楚，有问题，或者有指教的，都请和我多多交流，最后，我对这个士兵的巡逻分支画了一个示意图，供大家参考：

S — 选择节点   Se — 序列节点

————————————————————————
作者：Finney
Blog：AI分享站(http://www.aisharing.com/)
Email：finneytang@gmail.com
本文欢迎转载和引用，请保留本说明并注明出处
————————————————————————