P4095 [HEOI2013]Eden 的新背包问题
P4095 [HEOI2013]Eden 的新背包问题
题解
既然假定第 i 个物品不可以选,那么我们就设置两个数组
dpl[][] 正序选前i个物品,dpr[][] 倒序选前i个物品 ,价格不超过 j 的最大价值
然后正着反着跑 多重背包
最后答案考虑 i 之前的物品的价格和 i 之后的物品的价格,转移如下:

代码
#include<bits/stdc++.h> using namespace std; inline int read()
{
int ans=;
char last=' ',ch=getchar();
while(ch<''||ch>'') last=ch,ch=getchar();
while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
if(last=='-') ans=-ans;
return ans;
} int n,q,d,e,ans=;
int dpl[][],dpr[][];
//dpl[][]正序选前i个物品,dpr[][]倒序选前i个物品
struct node{
int a,b,c;
}thing[]; void pre() //多重背包
{
for(int i=;i<=n;i++) //正序背包
{
for(int j=;j<=;j++) dpl[i][j]=dpl[i-][j];
int x=,z=thing[i].c ;
while(x<=z){
for(int k=;k>=thing[i].a *x;k--)
dpl[i][k]=max(dpl[i][k],dpl[i][k-thing[i].a *x]+thing[i].b *x);
z-=x;
x<<=;
}if(z){
for(int k=;k>=thing[i].a *z;k--)
dpl[i][k]=max(dpl[i][k],dpl[i][k-thing[i].a *z]+thing[i].b *z);
}
}
for(int i=n;i>=;i--) //倒序背包
{
for(int j=;j<=;j++) dpr[i][j]=dpr[i+][j];
int x=,z=thing[i].c ;
while(x<=z){
for(int k=;k>=thing[i].a *x;k--)
dpr[i][k]=max(dpr[i][k],dpr[i][k-thing[i].a *x]+thing[i].b *x);
z-=x;
x<<=;
}if(z){
for(int k=;k>=thing[i].a *z;k--)
dpr[i][k]=max(dpr[i][k],dpr[i][k-thing[i].a *z]+thing[i].b *z);
}
}
} int main()
{
n=read();
for(int i=;i<=n;i++)
thing[i].a =read(),thing[i].b =read(),thing[i].c =read();
pre();
q=read();
for(int i=;i<=q;i++)
{
d=read()+; //输入编号是从0开始的
e=read();ans=;
for(int j=;j<=e;j++)
ans=max(ans,dpl[d-][j]+dpr[d+][e-j]);
printf("%d\n",ans);
}
return ;
}
后面附上听课笔记:
◦ N个物品,第i个物品有c[i]个,购买第i个物品需要a[i]元,可获利b[i]的价
值。有m个询问,每次询问:如果第x个物品禁止购买,你有y元的话,能
获得的最大价值是多少?询问之间互相独立。
◦ N<=1000,m<=3*10^5
>Solution
这是一个经典的问题
◦ 分治+背包
◦ 初始solve(1,n)
◦ 递归的函数到Solve(l,r),维护的dp数组,记录的是除去[l,r]外的物品的构成的背
包数组。
◦ Solve(l,mid)时,把[mid+1,r]内的物品加入dp数组。
◦ 我们这里定义的加入这个物品u,就是多考虑上这个物品之后构成的dp数组。
若是0/1背包的加入也就是做以下这个操作。
◦ For (int i=n;i>=w[u];i--) dp[i]=max(dp[i],dp[i-w[u]]+v[u]);
◦ 当l=r时,将对应所有的询问在dp数组查询即可。
◦ 单调队列优化的话,复杂度O(n*m*log(n)),每个物品被加进去log次,每次O(m)
代码实现
。由于你要分治求解,所以d表示深度
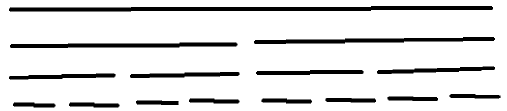
。
对于每次询问,ans得到答案,id[i]表示询问编号,S[i]表示题目所给出的y
。由于是分治,所以每次都先复制一遍再传递下去
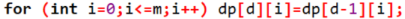
◦ Insert(dp,i):是在dp数组当中加入i号物品。
全部代码:
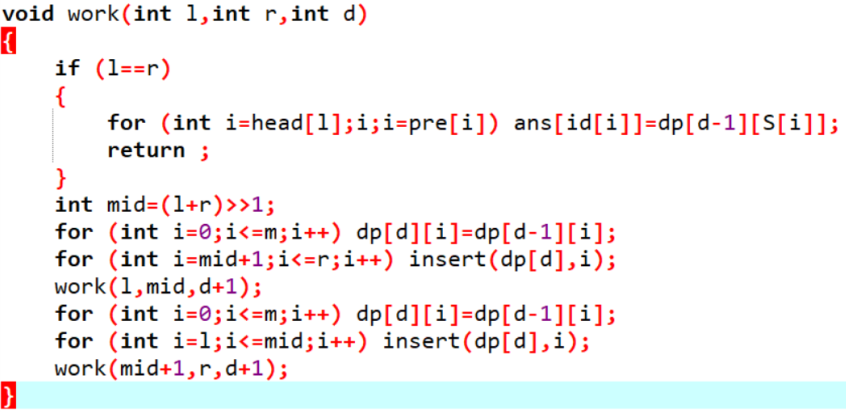
P4095 [HEOI2013]Eden 的新背包问题的更多相关文章
- luogu P4095 [HEOI2013]Eden 的新背包问题 多重背包 背包的合并
LINK:Eden 的新背包问题 就是一个多重背包 每次去掉一个物品 询问钱数为w所能买到的最大值. 可以对于每次Q暴力dp 利用单调队列优化多重背包 这样复杂度是Qnm的. 发现过不了n==10的点 ...
- LUOGU P4095 [HEOI2013]Eden 的新背包问题
题目描述 " 寄 没 有 地 址 的 信 ,这 样 的 情 绪 有 种 距 离 ,你 放 着 谁 的 歌 曲 ,是 怎 样 的 心 情 . 能 不 能 说 给 我 听 ." 失忆的 ...
- 题解——洛谷P4095 [HEOI2013]Eden 的新背包问题(背包)
思路很妙的背包 用了一些前缀和的思想 去掉了一个物品,我们可以从前i-1个和后i+1个推出答案 奇妙的思路 #include <cstdio> #include <algorithm ...
- Luogu P4095 [HEOI2013]Eden 的新背包问题 思维/动规
当时一直在想前缀和...多亏张队提醒... 从1到n背次包,保存每一个状态下的价值,就是不要把第一维压掉:再从n到1背一次,同样记住每种状态: 然后询问时相当于是max(前缀+后缀),当然前缀后缀中间 ...
- Luogu P4095 [HEOI2013]Eden的新背包问题
题目 求出从前往后的背包\(f_{i,j}\)和从后往前的背包\(F_{i,j}\). 那么对于询问\((d,e)\),答案就是\(\max\limits_{i=0}^e f_{d-1,i}+F_{d ...
- BZOJ 3163: [Heoi2013]Eden的新背包问题( 背包dp )
从左到右, 从右到左分别dp一次, 然后就可以回答询问了. ---------------------------------------------------------- #include< ...
- BZOJ3163&Codevs1886: [Heoi2013]Eden的新背包问题[分治优化dp]
3163: [Heoi2013]Eden的新背包问题 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 428 Solved: 277[Submit][ ...
- 洛谷P4095||bzoj3163 [HEOI2013]Eden 的新背包问题
https://www.luogu.org/problemnew/show/P4095 不太会.. 网上有神奇的做法: 第一种其实是暴力(复杂度3e8...)然而可以A.考虑多重背包,发现没有办法快速 ...
- bzoj 3163: [Heoi2013]Eden的新背包问题
Description "寄没有地址的信,这样的情绪有种距离,你放着谁的歌曲,是怎样的心心静,能不能说给我听."失忆的Eden总想努力地回忆起过去,然而总是只能清晰地记得那种思念的 ...
随机推荐
- 【异常】azkaban.executor.ExecutorManagerException: No active executors found
1 azkaban启动异常 没有找到活动的executors,需在MySQL数据库里设置端口为12321的executors表的active为1 update azkaban.executors ...
- 原生js制作播放器
以前 就想做一个播放器,一直没狠下心来,今天终于狠下心来,把这个做出来了(因为有点无聊) 做这个播放器 也百度了一下, 你叫我做,我肯定做不出来, 就算用jquery 我也做不出来. 以前也用过a ...
- 8. Object References, Mutability, and Recycling
1. Variables Are Not Boxes # Think variables as sticky notes a = [1, 2, 3] b = a a.append(4) print b ...
- javascript typeof instanceof
typeof用以获取一个变量或者表达式的类型,typeof一般只能返回如下几个结果: number,boolean,string,function(函数),object(NULL,数组,对象),und ...
- MUI 实现下拉刷新上拉加载的简单例子
话不多说,直接上代码与效果图吧. <!doctype html> <html> <head> <meta charset="utf-8"& ...
- [转]web.xml中servlet ,filter ,listener ,interceptor的作用与区别
原文链接:https://blog.csdn.net/netdevgirl/article/details/51483273 一.概念: 1.servlet:servlet是一种运行服务器端的java ...
- So easy RHCE
1.将VGSRV 拉伸为100MB VGSRV这个是逻辑卷的home分区,逻辑卷是可以随意拉伸的,但是需要注意的是拉伸之前必须使用umount卸载,否则系统会崩溃,虽然可以还原但是很麻烦,顺序不可 ...
- unity shader 剔除指定的颜色
Shader "MyShader/PaintingBGTransparency" { Properties{ _MainTex("Base (RGB)", 2D ...
- java中volatile关键字的含义(转载)
在java线程并发处理中,有一个关键字volatile的使用目前存在很大的混淆,以为使用这个关键字,在进行多线程并发处理的时候就可以万事大吉. Java语言是支持多线程的,为了解决线程并发的问题,在语 ...
- Linq to XML - C#生成XML
1.System.Xml.XmlDocument XML file转成字符串 string path3 = @"C:\Users\test.xml"; XmlDocument ...
